Физика атомного ядра и элементарных частиц
1. Закон радиоактивного распада
,
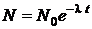где N0 – количество нераспавшихся ядер в начальный момент времени
(t = 0); N – количество нераспавшихся ядер по истечении времени t;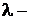 
постоянная радиоактивного распада.
2. Зависимость периода полураспада Т1/2 (промежуток времени, в течение которого количество нераспавшихся ядер уменьшается в 2 раза) от постоянной распада
.
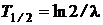3. Активность радиоактивного вещества
,
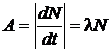где N – количество ядер, содержащихся в радиоактивном веществе.
4. Удельная активность радиоактивного вещества
,
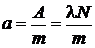где m – масса распадающегося вещества.
5. Среднее время жизни радиоактивного ядра (время, в течение которого количество нераспавшихся ядер уменьшается в е раз)
.
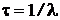6. Массовое число ядра (количество нуклонов в ядре)
,
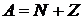где Z – зарядовое число ядра, равное количеству протонов в ядре; N – количество нейтронов в ядре.
7. Дефект массы ядра (разность между массой частиц, составляющих ядро, и массой самого ядра)
,
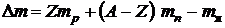где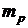 
– масса покоя протона; 
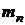– масса покоя нейтрона; 
– масса покоя ядра.
8. Энергия связи нуклонов в ядре
,
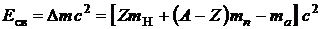где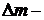 
дефект массы ядра; с – скорость света в вакууме; mH – масса покоя изотопа водорода 
; 
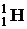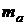– масса покоя атома.
9. Энергия ядерной реакции
,
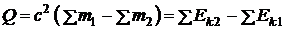где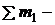 
сумма масс покоя частиц до реакции; 
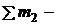сумма масс покоя частиц после реакции; 
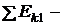сумма кинетических энергий частиц до реакции; 
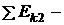сумма кинетических энергий частиц после реакции.
Если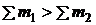 
, то реакция идет с выделением энергии (экзотермическая реакция), если 
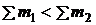, то реакция идет с поглощением энергии (эндотермическая реакция).
10. В ядерных реакциях выполняются законы сохранения:
суммарного количества нуклонов
;
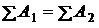зарядовых чисел
;
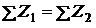релятивистской полной энергии
;
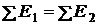импульса
,
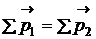где индекс 1 обозначает частицы до реакции, индекс 2 – частицы после реакции.
11. Решение задач по физике элементарных частиц основано на закономерностях, рассмотренных в предыдущих разделах курса. При решении некоторых задач необходимо использовать формулы специальной теории относительности.
Пример 9. Найти постоянную распада радона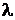 
, если известно, что количество атомов радона уменьшается за сутки на 18,2%.
Дано: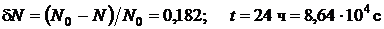 
.
Найти: .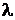
Решение. По закону радиоактивного распада
,
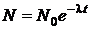где N0 – количество нераспавшихся ядер радона в момент времени t = 0;
N – количество нераспавшихся ядер по истечении времени t.
Количество ядер, распавшихся за время t, равно
.
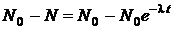Так как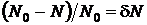 
, то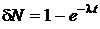 
. Тогда 
,
.
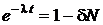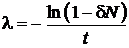Выполним анализ размерности
.
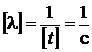Полученный результат соответствует действительности.
Сделаем подстановку числовых значений и произведем вычисления
.
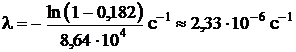Ответ: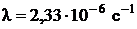 
.
Пример 10. Найти энергию связи, приходящуюся на один нуклон в ядре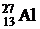 
.
Дано: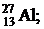 
Z = 13; А = 27; 
; 
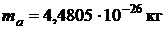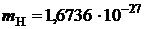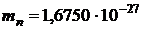кг; 
кг;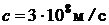 
.
Найти: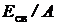 
.
Решение. Энергия связи нуклонов в ядре определяется выражением
,
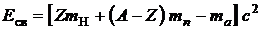где Z – зарядовое число ядра; А – массовое число ядра;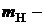 
масса изотопа водорода 
; 
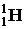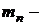масса покоя нейтрона; 
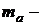масса покоя изотопа ;
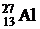с – скорость света в вакууме.
Найдем удельную энергию связи
.
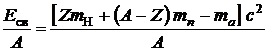Выполним анализ размерности
.
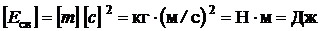Сделав подстановку числовых значений, получим
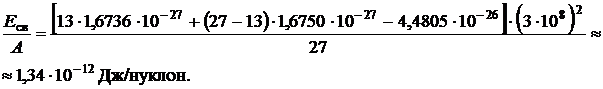
В атомной физике при решении задач часто используют внесистемные единицы: массы – атомная единица массы (а.е.м.); энергии – электрон-вольт (эВ) и мегаэлектрон-вольт (МэВ). Эти единицы допускаются к применению наравне с единицами СИ.
При использовании внесистемных единиц энергия связи нуклонов в ядре будет определяться формулой
,
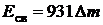где 931 – размерный коэффициент, МэВ/а.е.м; 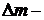дефект массы ядра, а. е. м.
Удельная энергия связи
.
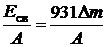Сделаем подстановку числовых значений и выполним вычисления
.
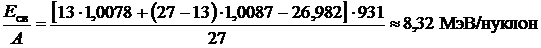Ответ: 
Пример 11. Определить энергию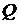 
ядерной реакции 
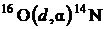. Выделяется или поглощается энергия в этой реакции?
Дано: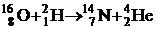 
.
Найти: Q.
Решение. В результате взаимодействия ядра кислорода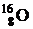 
и дейтрона d (ядро атома дейтерия 
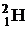) возникает ядро азота 
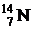и испускается 
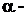частица (ядро атома гелия 
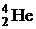). Энергия ядерной реакции определяется выражением
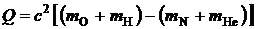, (1)
где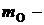 
масса покоя ядра кислорода; 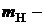масса покоя ядра дейтерия; 
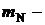масса покоя ядра азота; 
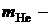масса покоя ядра гелия.
При выполнении расчетов массы ядер можно заменить массами нейтральных атомов. Масса нейтрального атома складывается из массы ядра и массы электронов, образующих электронную оболочку. При подстановке в уравнение (1) масс атомов массы электронов сокращаются
.
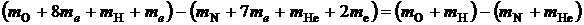В этом уравнении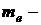 
масса покоя электрона. Таким образом, замена масс ядер массами атомов не влияет на результат вычислений.
При выполнении расчетов будем использовать внесистемные единицы. В этом случае 
Массы атомов и частиц, участвующих в реакции, возьмем из таблицы 3 приложения: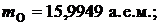 
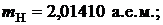
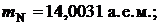
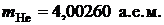
Выполним вычисления
.
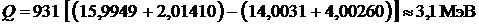Так как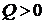 
, то энергия в реакции выделяется (экзотермическая реакция).
Ответ: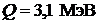 
.
Пример 12. При упругом центральном столкновении нейтрона с неподвижным ядром замедляющего вещества кинетическая энергия нейтрона уменьшилась в 1,4 раза. Найти массу ядер замедляющего вещества. Ответ записать в атомных единицах массы.
Дано: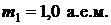 
; 
; 
; 
.
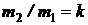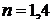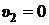Найти: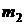 
.
Решение. Запишем законы сохра-нения импульса и энергии:
, 
,
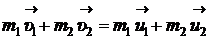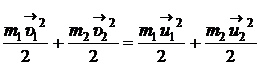где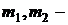 
массы покоя нейтрона и ядра замедляющего вещества;
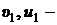скорости нейтрона до и после соударения соответственно;
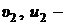скорости ядра замедляющего вещества до и после соударения соответственно.
Преобразуем эти уравнения, учитывая, что по условию задачи :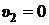
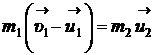; (1)
.
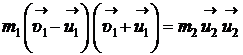Сопоставление последних двух выражений показывает, что
.
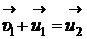Умножим все члены этого уравнения на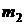
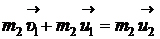(2)
Вычтем почленно из уравнения (1) уравнение (2):
.
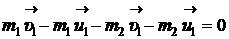Тогда
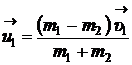. (3)
Масса ядер замедляющего вещества больше массы нейтрона, то есть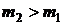 
. В этом случае, как видно из уравнения (3), вектор 
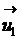будет направлен противоположно направлению вектора 
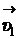. Запишем выражение (3) в проекциях на ось x (см. рис. 5):
.
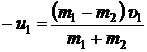Тогда
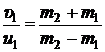. (4)
По условию задачи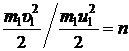 
, тогда 
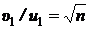. Так как 
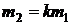, то, делая подстановку 
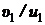и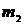 
в формулу (4), получим
.
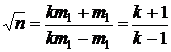Решим это уравнение относительно k:
.
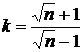Тогда
.
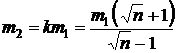Сделав подстановку числовых значений, получим
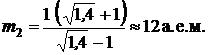
Ответ: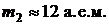 
(графит).
Пример 13. Электрон и позитрон, имевшие одинаковые кинетические энергии, равные 0,24 МэВ, при соударении превратились в два одинаковых фотона. Определить энергию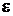 
каждого фотона и соответствующую ему длину волны .
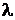Дано: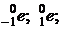 
.
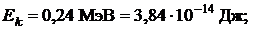
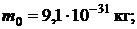
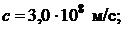
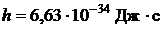Найти: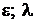 
.
Решение. Запишем уравнение реакции взаимодействия электрона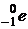 
и позитрона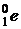 
,
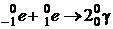где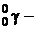 
фотон (квант электромагнитного излучения).
В ходе этой реакции выполняется закон сохранения релятивистской полной энергии
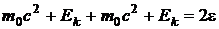, (1)
где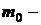 
масса покоя электрона (позитрона); 
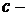скорость света в вакууме; 
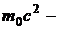энергия покоя электрона (позитрона); 
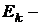кинетическая энергия электрона (позитрона).
Выразим из формулы (1) энергию фотона
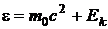. (2)
Так как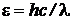 
, то
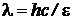, (3)
где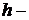 
постоянная Планка.
Подставим числовые значения физических величин в формулы (2) и (3) и выполним вычисления:
;
.
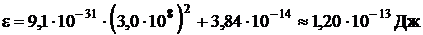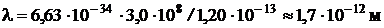Ответ: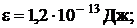 
.
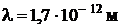