Подставив числовые значения, получим
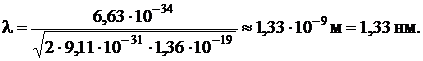
Ответ: 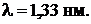
Пример 3. Электрон обладает кинетической энергией 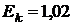 МэВ. Во сколько раз изменится длина волны де Бройля, если кинетическая энергия электрона уменьшится вдвое?
МэВ. Во сколько раз изменится длина волны де Бройля, если кинетическая энергия электрона уменьшится вдвое?
Дано:  МэВ = 1,63
МэВ = 1,63 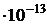 Дж;
Дж; 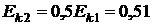 МэВ =
МэВ =
= 8,16 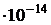 Дж;
Дж; 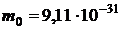 кг;
кг; 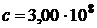 м/с.
м/с.
Найти: 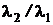 .
.
Решение. Длина волны де Бройля для микрочастицы определяется по формуле
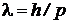 ,
,
где h – постоянная Планка; p – импульс микрочастицы.
Пусть р1 – импульс электрона в начальном состоянии, р2 – импульс электрона в конечном состоянии. Тогда
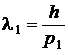 ,
, 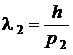 , а
, а 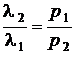 .
.
Найдем энергию покоя электрона
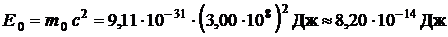 ,
,
где m0 – масса покоя электрона; с – скорость света в вакууме.
Так как кинетическая энергия соизмерима с энергией покоя электрона, то при решении задачи необходимо учитывать релятивистские эффекты. В этом случае связь импульса с кинетической энергией частицы определяется формулой
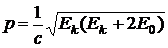 .
.
Импульсы электрона в начальном и конечном состояниях равны соответственно
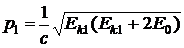 и
и  .
.
Вычисления показали, что практически 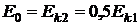 . Учитывая это, найдем отношение длин волн де Бройля
. Учитывая это, найдем отношение длин волн де Бройля
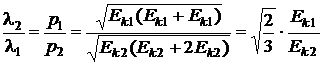 .
.
Анализ размерности полученного выражения показывает, что отношение 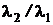 величина безразмерная, и убеждает в правдоподобности ответа.
величина безразмерная, и убеждает в правдоподобности ответа.
Выполним вычисления
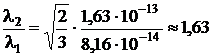 .
.
Ответ: 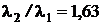 .
.
Пример 4. Используя соотношение неопределенностей, оценить минимальную энергию электрона 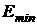 , находящегося в бесконечно глубокой одномерной прямоугольной «потенциальной яме» шириной l = 5
, находящегося в бесконечно глубокой одномерной прямоугольной «потенциальной яме» шириной l = 5  .
.
Дано: 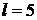
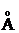
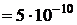 м;
м; 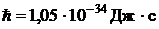 ;
; 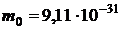 кг.
кг.
Найти: 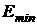 .
.
Решение. Соотношение неопределенностей Гейзенберга для координаты и импульса в случае одномерной задачи 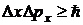 позволяет оценить неопределенность импульса электрона
позволяет оценить неопределенность импульса электрона
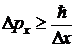 ,(1)
,(1)
где 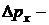 неопределенность импульса;
неопределенность импульса; 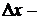 неопределенность координаты;
неопределенность координаты; 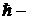 постоянная Планка h, деленная на 2
постоянная Планка h, деленная на 2 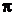 .
.
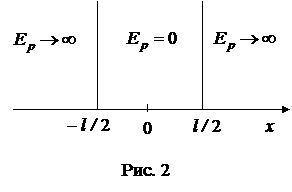 Так как ширина «потенциальной ямы» равна l, и электрон находится в этой «яме», то неопределенность его координаты равна
Так как ширина «потенциальной ямы» равна l, и электрон находится в этой «яме», то неопределенность его координаты равна 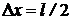 (рис. 2). Потенциальная энергия электрона
(рис. 2). Потенциальная энергия электрона  внутри «ямы» равна нулю, следовательно, его полная механическая энергия Е равна кинетической
внутри «ямы» равна нулю, следовательно, его полная механическая энергия Е равна кинетической  . За пределами «ямы», ограниченной бесконечно высокими «стенками»,
. За пределами «ямы», ограниченной бесконечно высокими «стенками», 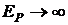 .
.
Связь импульса p с кинетической энергией электрона для нерелятивистского случая имеет вид (учитываем, что по условию задачи 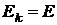 )
)
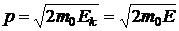 ,
,
где m0 – масса покоя электрона.
Выразим полную энергию Е в виде
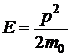 .
.
Из этого уравнения видно, что энергия электрона тем меньше, чем меньше его импульс. Неопределенность значения импульса равна 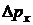 . Минимальное значение импульса электрона
. Минимальное значение импульса электрона 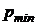 должно быть не меньше
должно быть не меньше 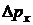 , то есть
, то есть 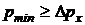 . Учитывая это, можем записать
. Учитывая это, можем записать
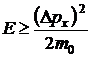 .
.
Сделав подстановку 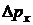 из уравнения (1) с учетом того, что
из уравнения (1) с учетом того, что 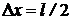 , придем к уравнению
, придем к уравнению
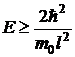 .
.
Следовательно, минимальная энергия электрона
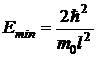 .
.
Анализ размерности убеждает, что ответ правдоподобен, так как энергия действительно измеряется в джоулях:
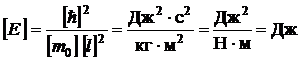 .
.
Подставим числовые значения в конечную формулу и выполним вычисления (оцениваем лишь порядок вычисляемой величины)
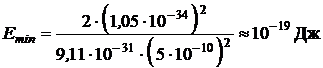 .
.
Ответ: 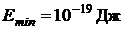 .
.
Пример 5. Электрон находится в бесконечно глубокой одномерной прямоугольной «потенциальной яме» с непроницаемыми «стенками». Ширина «ямы» l = 37,8 эВ. Определить, на каком энергетическом уровне находится электрон. Чему равна плотность вероятности обнаружения электрона в середине «ямы»?
Дано: 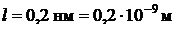 ;
; 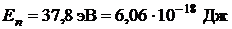 ;
; 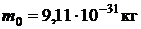 ;
; 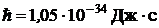 .
.
Найти: n; w.
Решение: Запишем уравнение Шредингера для стационарных состояний. Для рассматриваемой одномерной задачи это уравнение имеет вид
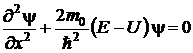 ,
,
где 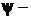 координатная часть волновой функции, зависящая только от x; Е – полная энергия электрона; U – потенциальная энергия электрона;
координатная часть волновой функции, зависящая только от x; Е – полная энергия электрона; U – потенциальная энергия электрона; 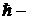 постоянная Планка h, деленная на 2π.
постоянная Планка h, деленная на 2π.
Электрон находится в «яме», где его потенциальная энергия
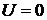 (рис. 3). За пределами «ямы», ограниченной бесконечно высокими «стенками»,
(рис. 3). За пределами «ямы», ограниченной бесконечно высокими «стенками», 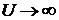 . Электрон не может проникнуть за пределы «ямы», поэтому вероятность его обнаружения (а, следовательно, и волновая функция) за пределами «ямы» равна нулю. Из условия непрерывности волновой функции следует, что
. Электрон не может проникнуть за пределы «ямы», поэтому вероятность его обнаружения (а, следовательно, и волновая функция) за пределами «ямы» равна нулю. Из условия непрерывности волновой функции следует, что 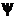 должна быть равна нулю и на границах «ямы»:
должна быть равна нулю и на границах «ямы»:
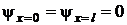 .
.
В пределах «ямы» 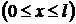 уравнение Шредингера имеет вид
уравнение Шредингера имеет вид
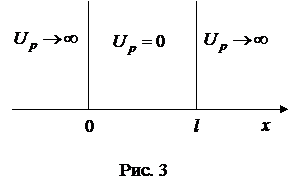
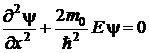 . (1)
. (1)
Это уравнение, описывающее дви-жение электрона в одномерной «потенциальной яме», удовлетворяется при ди-скретных значениях энергии электрона
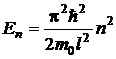
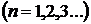 ,
,
где n – квантовые числа, определяющие энергетические уровни электрона.
Выразим из этой формулы n:
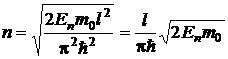 .
.
Анализ размерности правой части полученного выражения показывает, что n – величина безразмерная, и это соответствует действительности.
После подстановки числовых значений, данных в условии задачи, получим
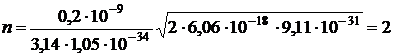 .
.
Решение дифференциального уравнения (1) для рассматриваемой задачи имеет вид
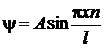 .
.
Коэффициент А находим из условия нормировки
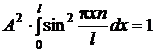 .
.
В результате интегрирования получаем 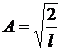 , следовательно:
, следовательно:
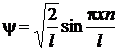
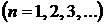 .
.
Плотность вероятности обнаружения электрона на различных расстояниях x от стенок «ямы» для рассматриваемой задачи равна
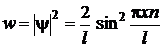 .
.
Выполним анализ размерности (выражение под знаком sin безразмерное):
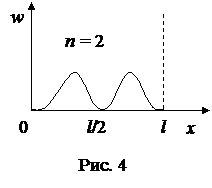
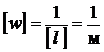 .
.
Полученная единица соответствует искомой величине.
Вычислим значение w при n = 2 для
x = l/2:
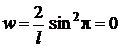 .
.
Такой результат означает, что в состоянии с n = 2 электрон не может находиться в середине «ямы». Зависимость плотности вероятности обнаружения электрона на различных расстояниях от стенок «ямы» приведена на рис. 4.
Ответ: n = 2; w = 0.
Пример 5. Пси-функция некоторой частицы имеет вид 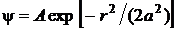 , где r – расстояние частицы от силового центра,
, где r – расстояние частицы от силового центра, 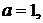 0
0 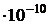 м – константа. Найти значение коэффициента А и наиболее вероятное расстояние rвер частицы от центра.
м – константа. Найти значение коэффициента А и наиболее вероятное расстояние rвер частицы от центра.
Дано: 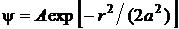 ; а = 1,0
; а = 1,0 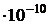 м.
м.
Найти: А; rвер.
Решение. Движение микрочастицы в центральном силовом поле (например, движение электрона в поле положительно заряженного ядра) описывается уравнением Шредингера в сферических координатах. По условию задачи функция 
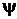 зависит только от r и не зависит от углов
зависит только от r и не зависит от углов 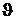 и
и 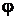 . В этом случае уравнение Шредингера для стационарных состояний принимает вид
. В этом случае уравнение Шредингера для стационарных состояний принимает вид
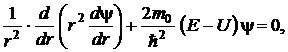
где r – расстояние микрочастицы от силового центра; m0 – масса покоя микрочастицы; 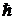 – постоянная Планка h , деленная на 2
– постоянная Планка h , деленная на 2 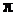 ; Е – полная энергия микрочастицы; U – потенциальная энергия микрочастицы.
; Е – полная энергия микрочастицы; U – потенциальная энергия микрочастицы.
Перепишем уравнение Шредингера, выполнив дифференцирование в первом слагаемом:
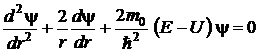 .
.
Решение этого дифференциального уравнения по условию задачи имеет вид
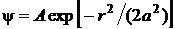 .
.
Коэффициент А найдем из условия нормировки пси-функции, которое для рассматриваемой задачи запишем в виде
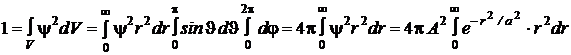 ,
,
где dV - элемент объема в сферических координатах 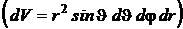 .
.
Интеграл в полученном выражении равен 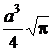 (табл. 6 приложения), следовательно:
(табл. 6 приложения), следовательно:
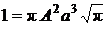 и
и 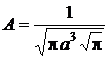 .
.
Выполним анализ размерности полученного выражения
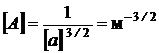 .
.
Анализ размерности подтверждает правдоподобность ответа. Действительно, квадрат модуля волновой функции имеет смысл плотности вероятности обнаружения микрочастицы
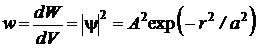 ,
,
где dW – вероятность нахождения частицы в элементе объема 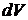 .
.
Так как размерность 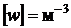 , то размерность
, то размерность 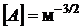 .
.
Выполним вычисления
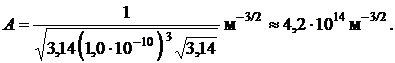
Вероятность нахождения микрочастицы на расстоянии между r и r+dr от силового центра в любом направлении определяется формулой
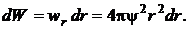
Следовательно, плотность вероятности
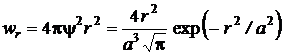 .
.
Из формулы видно, что плотность вероятности 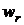 обращается в нуль при r = 0 и асимптотически стремится к нулю при
обращается в нуль при r = 0 и асимптотически стремится к нулю при 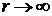 . Наиболее вероятное расстояние rвер частицы от силового центра найдем из условия, что при r = rвер плотность вероятности должна быть максимальна. Для этого исследуем функцию
. Наиболее вероятное расстояние rвер частицы от силового центра найдем из условия, что при r = rвер плотность вероятности должна быть максимальна. Для этого исследуем функцию 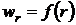 на экстремум. Найдем первую производную
на экстремум. Найдем первую производную 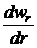 и приравняем ее к нулю
и приравняем ее к нулю
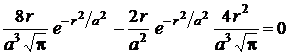 ;
; 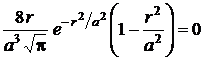 .
.
Это равенство выполняется при r = 0; 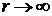 ; r = a. Первые два решения соответствуют минимумам функции
; r = a. Первые два решения соответствуют минимумам функции 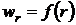 . Следовательно, наиболее вероятное расстояние микрочастицы от силового центра
. Следовательно, наиболее вероятное расстояние микрочастицы от силового центра 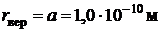 .
.
Ответ: 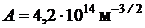 ; rвер = 1,0
; rвер = 1,0 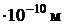 .
.
ЭЛЕМЕНТЫ КВАНТОВОЙ СТАТИСТИКИ
И ФИЗИКИ ТВЕРДОГО ТЕЛА
1. Распределение свободных электронов в металле по состояниям с различной энергией при Т = 0 К
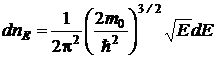 ,
,
где dnE – количество свободных электронов в единице объема металла (концентрация электронов), энергии которых заключены в пределах от Е до E + dE; m0 – масса покоя электрона.
2. Энергия Ферми в металле при Т = 0 К
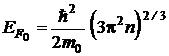 ,
,
где n – концентрация электронов проводимости в металле.
3. Температура вырождения (температура Ферми)
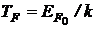 ,
,
где 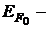 энергия Ферми при Т = 0 К; k – постоянная Больцмана.
энергия Ферми при Т = 0 К; k – постоянная Больцмана.
Температурой вырождения ТF называют температуру, ниже которой проявляются квантовые свойства электронного газа. Если T >> 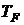 , то поведение системы частиц подчиняется классической статистике.
, то поведение системы частиц подчиняется классической статистике.
4. Температурная зависимость удельной электрической проводимости собственных полупроводников
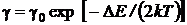 ,
,
где 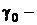 множитель, мало изменяющийся с изменением температуры;
множитель, мало изменяющийся с изменением температуры; 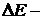 ширина запрещенной зоны.
ширина запрещенной зоны.
Пример 7. Определить отношение концентраций свободных электронов при Т = 0 К в литии n1 и цезии n2 , если известно, что уровни Ферми в этих металлах соответственно равны 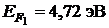 и
и 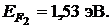
Дано: 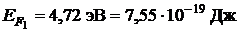 ;
; 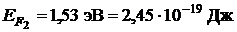 .
.
Найти: n1/n2.
Решение. Уровень Ферми при абсолютном нуле определяется выражением
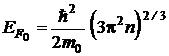 ,
,
где 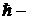 постоянная Планка h, деленная на 2π ;
постоянная Планка h, деленная на 2π ; 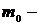 масса покоя электрона;
масса покоя электрона; 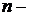 количество свободных электронов в единице объема металла.
количество свободных электронов в единице объема металла.
Используя эту формулу, запишем соотношения, определяющие концентрации n1 и n2 свободных электронов в литии и цезии:
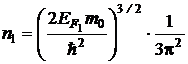 ;
; 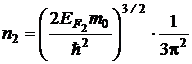 .
.
Выполним анализ размерности
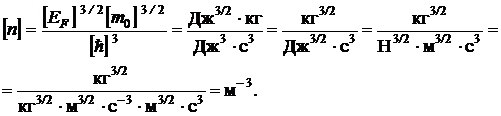
Полученный результат соответствует действительности.
Найдем отношение концентраций свободных электронов
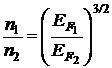 .
.
Подставим в это выражение числовые значения и выполним вычисления
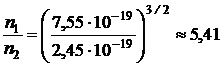 .
.
Ответ: 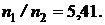
Пример 8. Найти относительное количество ΔN/N свободных электронов в металле, кинетическая энергия которых отличается от энергии Ферми не более, чем на η = 2,0%. Температура металла Т = 0 К.
Дано: Т = 0 К; η = 0,02 (2,0%).
Найти: ∆N/N.
Решение. Распределение свободных электронов в металле по состояниям с различной энергией при Т = 0 К имеет вид
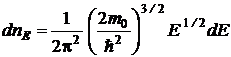 ,
,
где dnE – концентрация свободных электронов, энергии которых заключены в пределах от Е до Е + dE; m0 – масса покоя электрона; ħ – постоянная Планка h, деленная на 2π.
Концентрацию свободных электронов в металле найдем путем интегрирования
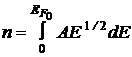 ,
,
где 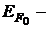 энергия Ферми при Т = 0 К;
энергия Ферми при Т = 0 К; 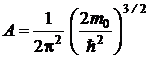 .
.
Если образец металла имеет объем  , то количество свободных электронов в этом образце
, то количество свободных электронов в этом образце
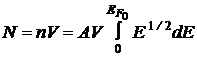 .
.
Концентрация свободных электронов, энергии которых отличаются от энергии Ферми не более, чем на 2%, равна
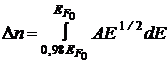 .
.
Количество таких электронов в образце металла объемом 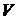
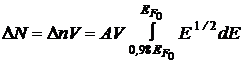 .
.
Найдем относительное количество свободных электронов, кинетическая энергия которых отличается от энергии Ферми не более, чем на 2%:
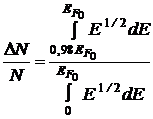 .
.
Произведя вычисления, получим
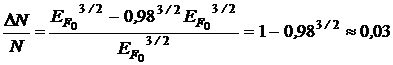 .
.
Ответ: 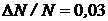 (или 3%).
(или 3%).
