Основы электродинамики. магнитное поле. электромагнитные явления. электромагнитные волны.
Примеры решения задач
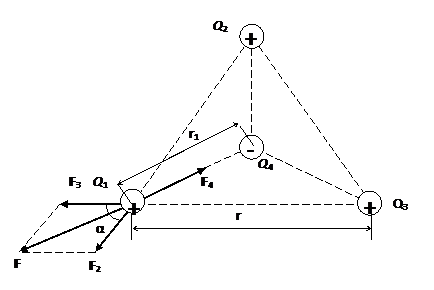
 Пример 1. Три точечных заряда Q1 = Q2 = Q 3 = 1 нКл расположены в вершинах равностороннего треугольника. Какой заряд Q4 нужно поместить в центре треугольника, чтобы указанная система зарядов находилась в равновесии?
Пример 1. Три точечных заряда Q1 = Q2 = Q 3 = 1 нКл расположены в вершинах равностороннего треугольника. Какой заряд Q4 нужно поместить в центре треугольника, чтобы указанная система зарядов находилась в равновесии?
Дано: Решение.
 Q1 = Q2 = Q 3 = 1 нКл Все три заряда, расположенные по вершинам
Q1 = Q2 = Q 3 = 1 нКл Все три заряда, расположенные по вершинам
Q4 - ? треугольника, находятся в одинаковых условиях.
Поэтому достаточно выяснить, какой заряд следует поместить в центре
треугольника, чтобы какой-нибудь один из трех зарядов, например Q1, находился в равновесии. Заряд Q1 будет находиться в равновесии, если векторная сумма действующих на него сил равна нулю (рис. 2).
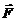 2 +
2 + 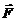 3 +
3 + 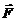 4 =
4 = 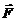 +
+ 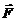 4 = 0 (1)
4 = 0 (1)
 где
где  2,
2,  3,
3, 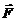 4 – силы, с которыми
4 – силы, с которыми
соответственно действуют на
заряд Q1 заряды Q2, Q3, Q4;
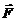 – равнодействующая сил
– равнодействующая сил
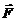 2 и
2 и 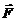 3.
3.
| |
Рис.2
Так как силы 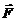 и
и 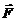 4 направлены по одной прямой в противоположные стороны, то векторное равенство (1) можно заменить скалярным.
4 направлены по одной прямой в противоположные стороны, то векторное равенство (1) можно заменить скалярным.
F – F4 = 0, откуда F4 = F.
Выразив в последнем равенстве F через F2 и F3 и учитывая, что F3 = F2, получим
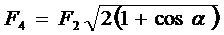 .
.
Применив закон Кулона и имея в виду, что Q1 = Q2 = Q 3 , найдем
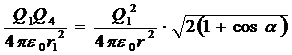 , откуда
, откуда
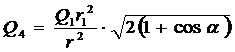 . (2)
. (2)
Из геометрических построений в равностороннем треугольнике следует, что
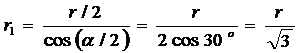 , соs α = cos 60o = 1/2.
, соs α = cos 60o = 1/2.
С учетом этого формула (2) примет вид
Q4 =  Q1 /
Q1 / 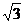 .
.
Произведем вычисления.
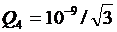 = 5,77∙ 10 – 10 Кл = 577 пКл.
= 5,77∙ 10 – 10 Кл = 577 пКл.
Ответ: Q4 = 577∙ 10 – 12 Кл = 577 пКл
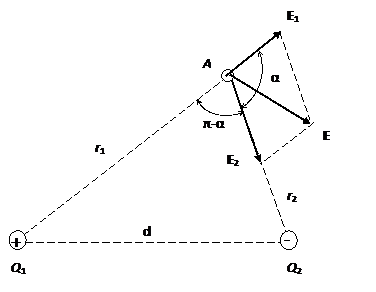
Пример 2. Два точечных электрических заряда Q 1 = 1 нКл и Q 2 = - 2 нКл находятся в воздухе на расстоянии d = 10 см друг от друга.
Определить напряженность 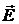 и потенциал φ поля, создаваемого этими зарядами в точке А, удаленной от заряда Q 1 на расстояние r1 = 9 см и от заряда Q 2 на r2 = 7 см.
и потенциал φ поля, создаваемого этими зарядами в точке А, удаленной от заряда Q 1 на расстояние r1 = 9 см и от заряда Q 2 на r2 = 7 см.
 Дано: Решение.
Дано: Решение.
Q 1 = 1 нКл
Q 2 = - 2 нКл
d = 10 см
r1 = 9 см
r2 = 7 см

Е = ? φ = ?
Рис.3
Согласно принципу суперпозиции электрических полей, каждый заряд создает поле независимо от присутствия в пространстве других зарядов. Поэтому напряженность 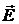 электрического поля в искомой точке может быть найдена как геометрическая сумма напряженностей
электрического поля в искомой точке может быть найдена как геометрическая сумма напряженностей 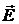 1 и
1 и 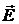 2 полей, создаваемых каждым зарядом в отдельности:
2 полей, создаваемых каждым зарядом в отдельности: 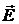 =
= 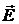 1 +
1 + 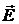 2. Напряженность электрического поля, создаваемого в воздухе (ε = 1) зарядами Q 1 и Q 2 ,
2. Напряженность электрического поля, создаваемого в воздухе (ε = 1) зарядами Q 1 и Q 2 ,
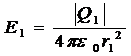 , (1)
, (1)
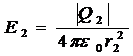 . (2)
. (2)
Вектор 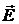 1 (рис. 9) направлен по силовой линии от заряда Q 1 , так как этот заряд положителен; вектор
1 (рис. 9) направлен по силовой линии от заряда Q 1 , так как этот заряд положителен; вектор 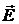 2 направлен также по силовой линии, но к заряду Q 2 , так как этот заряд отрицателен.
2 направлен также по силовой линии, но к заряду Q 2 , так как этот заряд отрицателен.
Модуль вектора 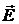 найдем по формуле векторной алгебры.
найдем по формуле векторной алгебры.
Е = 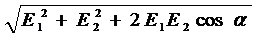 , (3)
, (3)
где α – угол между векторами 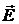 1 и
1 и 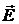 2;
2;
сos α может быть найден из треугольника со сторонами r1 , r2 и d по теореме косинусов (рис. 3)
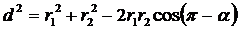 ; сos (π-α) = - cos α . Тогда
; сos (π-α) = - cos α . Тогда
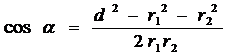 .
.
Во избежание громоздких записей удобно значение cos α вычислить отдельно.
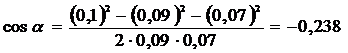 .
.
Подставляя выражение Е1 из (1) и Е2 из (2) в (3) и вынося общий множитель 1/(4πε0) за знак корня, получаем
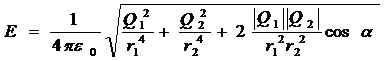 . (4)
. (4)
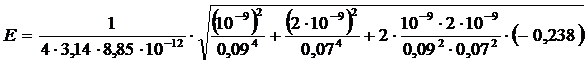 = = 3,58 ∙ 10 3 В/м = 3,58 кВ/м.
= = 3,58 ∙ 10 3 В/м = 3,58 кВ/м.
В соответствии с принципом суперпозиции электрических полей потенциал φрезультирующего поля, создаваемого двумя зарядами Q 1 и Q 2 , равен алгебраической сумме потенциалов
φ = φ1 + φ2. (5)
Потенциал электрического поля, создаваемого в вакууме точечным зарядом Q на расстоянии r от него, выражается формулой
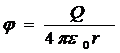 . (6)
. (6)
Согласно формулам (5) и (6) получим
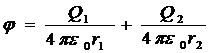 , или
, или
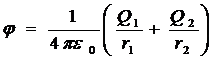 .
.
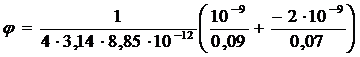 = - 157 В.
= - 157 В.
Ответ: Е = 3,58 кВ/м; φ = - 157 В
Пример 3. На пластинах плоского конденсатора находится заряд Q = 20 нКл. Площадь S каждой пластины конденсатора равна 100 см 2, диэлектрик – воздух. Определить силу F, с которой притягиваются пластины. Поле между пластинами считать однородным.
 Дано: Решение.
Дано: Решение.
Q = 20 нКл Заряд Q одной пластины находится в поле
S =100 см 2 напряженностью Е, созданном зарядом другой пластины
 F -? конденсатора. Следовательно, на первый заряд действует
F -? конденсатора. Следовательно, на первый заряд действует
сила
F = Q ∙Е. (1)
Так как
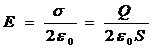 ,
,
где σ - поверхностная плотность заряда пластины, то формула (1) примет вид
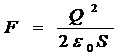 .
.
Произведем вычисления.
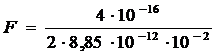 = 22,6∙ 10 -4 Н
= 22,6∙ 10 -4 Н
Ответ: F = 22,6∙ 10 -4 Н
Пример 4. Электрическое поле создано длинным цилиндром радиусом R = 1 см, равномерно заряженным с линейной плотностью τ = 10 нКл/м. Определить разность потенциалов двух точек этого поля, находящихся на расстоянии a1 = 0,5 см и a2 = 2 см от поверхности цилиндра, в средней его части.
 Дано: Решение.
Дано: Решение.
R = 1 см Для определения разности потенциалов
τ=10 нКл/м воспользуемся соотношением между напряженностью
a 1 = 0,5 см поля и изменением потенциала.
 a 2 = 2 см
a 2 = 2 см 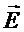 = -
= - 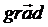 φ;.
φ;.
φ 1 - φ 2 = ? Для поля с осевой симметрией, каким является поле
цилиндра, это соотношение можно записать в виде
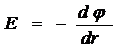 , или dφ = - E dr.
, или dφ = - E dr.
Интегрируя это выражение, найдем разность потенциалов двух точек, отстоящих на расстояниях r 1 и r 2 от оси цилиндра
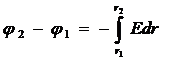 . (1)
. (1)
Так как цилиндр длинный и точки взяты вблизи его средней части, то для выражения напряженности поля можно воспользоваться формулой напряженности поля, создаваемого бесконечно длинным цилиндром.
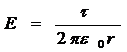 .
.
Подставив выражение Е в (1), получим
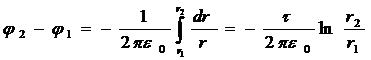 ,
,
или
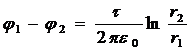 . (2)
. (2)
Произведем вычисления, учитывая, что величины r 1 и r 2 , входящие в формулу (2) в виде отношения, можно выразить в сантиметрах (r 1 = R + a 1 = 1,5 см , r 2 = R + a 2 = 3 см ) .
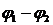 = 1∙ 10 – 8 ∙1,8 ∙ 10 10 ∙ ln (3/1,5) = 1,8 ∙ 10 2 ∙ 2,3 ln 2 = 125 В.
= 1∙ 10 – 8 ∙1,8 ∙ 10 10 ∙ ln (3/1,5) = 1,8 ∙ 10 2 ∙ 2,3 ln 2 = 125 В.
Ответ: 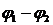 = 125 В
= 125 В
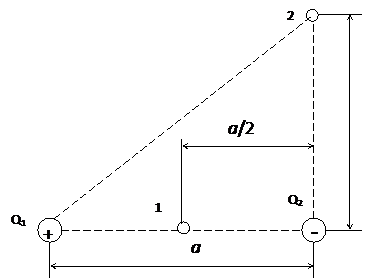
Пример 5. Электрическое поле создается двумя зарядами Q1 = 4 мкКл и Q2 = - 2 мкКл , находящимися на расстоянии а = 0,1 м друг от друга. Определить работу А1, 2 сил поля по перемещению заряда Q = 100 нКл из точки 1 в точку 2 (рис. 4).
 Дано: Решение.
Дано: Решение.
 Q1 = 4 мкКл
Q1 = 4 мкКл
Q2 = - 2 мкКл
Q = 100 нКл
 а = 0,1 м
а = 0,1 м
А1, 2 - ?
Рис. 4
Для определения работы А1, 2 сил поля воспользуемся соотношением
А1, 2 =Q 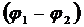 .
.
Применяя принцип суперпозиции электрических полей, определим потенциалы φ 1 и φ 2 точек 1 и 2 поля
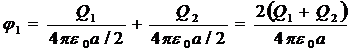 ;
;
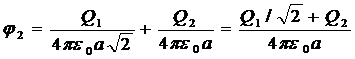 .
.
Тогда
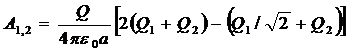 ,
,
или
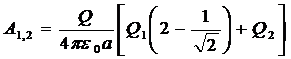 .
.
Проверим, дает ли правая часть равенства единицу работы (Дж).
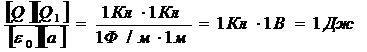
Подставим числовые значения физических величин в СИ (Q = 100∙10 – 9 Кл , Q1 = 4∙10 – 6 Кл , Q 2 = -2∙10 – 6 Кл , а = 0,1 м , 1/(4πε0)= 9 ∙ 10 9 м/Ф ) и произведем вычисления.
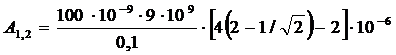 =28,6 мДж
=28,6 мДж
Ответ: А1, 2 = 28,6 мДж
ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ № 2
Таблица вариантов к контрольной работе №2
| Алфавит | Номера задач по первой букве | |||||
| фамилии | имени | отчества | ||||
| А,К,Ф | ||||||
| Б,Л,Х | ||||||
| В,М,Ц | ||||||
| Г,Н,Ч | ||||||
| Д,О,Ш | ||||||
| Е,П,Щ | ||||||
| Ё,Р | ||||||
| Ж,С, Э | ||||||
| З,Т,Ю | ||||||
| И,У,Я |
Например, студент Сиделов Никита Игоревич должен решить следующие задачи: по первой букве фамилии С – (203, 218), по первой букве имени Н – (227, 234) и по первой букве отчества И – (241, 260).
201. На проводник длиной 50 см с током 2 А однородное магнитное поле с магнитной индукцией 0,7 Тл действует с силой 0,05 Н. Определить угол между направлением тока и вектором магнитной индукции.
202. На провод обмотки электродвигателя при силе тока 20 А действует сила 1 Н. Определите магнитную индукцию в месте расположения провода, если его длина 20 см.
203. По горизонтально расположенному проводнику длиной 20 см и массой 4 г течет ток 10 А. Найдите индукцию (модуль и направление) магнитного поля, в которое нужно поместить проводник, чтобы сила тяжести уравновесилась силой Ампера.
204. На провод обмотки якоря электродвигателя при силе тока 20 А действует сила 7 Н. Определите магнитную индукцию поля в месте расположения провода, если длина провода 0,2 м.
205. С какой силой действует магнитное поле с индукцией 10 мТл на проводник, в котором сила тока 50 А, если длина активной части проводника 0,1 м? Поле и ток взаимно перпендикулярны.
206. Однородное магнитное поле с индукцией 200 мТл действует на помещенный в него проводник длиной 50 см с силой 0,7 мН. Определите силу тока в проводнике, если угол между направлением тока и индукцией магнитного поля равен 450.
207. На прямолинейный проводник, расположенный в однородном магнитном поле с индукцией 0,05 Тл под углом 30º к полю, действует сила 0,5 Н при пропускании по нему тока 20 А. Какова длина проводника?
208. Проводник длиной 0,15 м с током 8 А перпендикулярен вектору магнитной индукции однородного поля, модуль которого 0,4 Тл. Определить работу поля по перемещению проводника на 2,5 мм.
209. С какой средней силой действовало магнитное поле с индукцией 0,2 Тл на проводник длиной 0,3 м, если в проводнике ток равномерно возрастал от нуля до 10 А?
210. По круговому витку радиусом 10 см циркулирует ток 4 А. Определить напряженность и индукцию магнитного поля в центре витка.
211. Квадратная рамка помещена в однородное магнитное поле. Нормаль к плоскости рамки составляет с направлением магнитного поля угол 600. Сторона рамки 19 см. Определите индукцию магнитного поля, если известно, что среднее значение ЭДС индукции, возникающей в рамке при выключении поля в течение 0,01 с, равно 50 мВ.
212. Проволочный виток диаметром 5 см и сопротивлением 0,02 Ом находится в однородном магнитном поле с индукцией 0,3 Тл. Плоскость витка составляет угол 400 с линиями индукции. Какой заряд протечет по витку при равномерном уменьшении магнитного поля до нуля?
213. Кольцо из проволоки сопротивлением 10–3 Ом находится в однородном магнитном поле с индукцией 0,4 Тл. Определить заряд, который потечет по кольцу, если его выдернуть из поля. Площадь кольца 10 см2, а плоскость составляет угол 90º с линиями магнитной индукции.
214. Проволочный виток радиусом 4 см находится в однородном магнитном поле с индукцией 0,2 Тл. Плоскость витка составляет с линиями индукции угол 30º. Определить поток магнитной индукции, пронизывающий виток.
215. При равномерном изменении магнитного потока, пронизывающего контур проводника на 6,6 Вб, ЭДС индукции в контуре была равна 7,2 В. Найти время изменения магнитного потока.
216. С какой скоростью надо перемещать проводник, длина активной части которого 1 м под углом 60º к линиям индукции магнитного поля, чтобы в проводнике возбуждалась ЭДС индукции в 7 В? Индукция магнитного поля 0,2 Тл.
217. Самолет, имеющий размах крыльев 31,7 м, летит горизонтально со скоростью 400 км/ч. Определить разность потенциалов на концах крыльев, если вертикальная составляющая индукции магнитного поля Земли 5·10-5 Тл.
218. Магнитный поток, пронизывающий замкнутый проволочный контур с сопротивлением 0,5 Ом, равномерно увеличился с 0,2 мВб до 7 мВб. Какой заряд прошел за это время через поперечное сечение проводника при равномерном изменении потока. Сила тока, ЭДС – постоянны.
219. Горизонтальный стержень длиной 1 м вращается вокруг вертикальной оси, проходящей через один из его концов. Ось вращения параллельна магнитному полю с индукцией 50 мкТл. При какой частоте вращения стержня разность потенциалов на его концах U = 7 мВ?
220. Автомобиль движется со скоростью 120 км/ч. Определить разность потенциалов на концах передней оси машины, если длина оси 180 см, а вертикальная составляющая вектора индукции магнитного поля земли равна 5·10-5 Тл.
221. Электрон движется в однородном магнитном поле с индукцией 5·10-3 Тл со скоростью 107 м/с, направленной перпендикулярно линиям индукции. Найти силу, действующую на электрон в магнитном поле, и радиус окружности, по которой он движется.
222. Найдите кинетическую энергию протона, движущегося в магнитном поле по окружности радиусом 50 см. Индукция поля 100 мТл.
223. В направлении, перпендикулярном линиям магнитной индукции, влетает в магнитное поле электрон со скоростью 107 м/с. Найти индукцию поля, если электрон описал в поле окружность радиусом 1 см.
224. Электрон, ускоренный разностью потенциалов U = 6 кВ, влетает в однородное магнитное поле под углом в 30º. Найти радиус винтовой линии, если В = 1,3 Тл.
225. Электрон, ускоренный разностью потенциалов U = 10 кВ, влетает в однородное магнитное поле под углом в 60º. Найти шаг винтовой линии, если В = 1,3 Тл.
226. Магнитное поле с В=5 Тл, направлено перпендикулярно электрическому полю напряженностью Е = 10 В/см. Пучок электронов летит с некоторой скоростью V, в пространство, где расположены эти поля, их скорость перпендикулярна плоскости, в которой лежат Е и В. Найти скорость электронов, если при одновременном действии обоих полей пучок электронов не испытывает отклонения.
227. Циклотрон предназначен для ускорения протонов до энергии 5 МэВ. Определить наибольший радиус орбиты, по которой движется протон, если индукция магнитного поля циклотрона 1 Тл.
228. Сравнить отношение q/m для протона и электрона, если они, влетая со скоростью 106 м/с, в однородное магнитное поле напряженностью 3 А/м, движутся по окружности радиуса 9 см.
229. Магнитное поле с В=3 Тл направлено перпендикулярно электрическому с напряженностью Е = 6 В/см. Пучок электронов влетает с некоторой скоростью v, в пространство, где расположены эти поля. Скорость электронов перпендикулярна плоскости, в которой лежат Е и В. Найти радиус кривизны траектории электронов, если включено только магнитное поле.
230. Найти отношение q/m для заряженной частицы, если она, влетая со скоростью 108 м/с в однородное магнитное поле напряженностью 2,5 А/м, движется по окружности радиуса 8,3 см.
231. Поток магнитной индукции сквозь соленоид равен 5·10-6 Вб. Найти магнитный момент этого соленоида, если его длина 25 см.
232. Сколько ампер-витков потребуется для того, чтобы внутри соленоида малого диаметра и длиною 30 см объемная плотность энергии магнитного поля стала равна 7,75 Дж/м3.
233. В обмотке трансформатора с индуктивностью 0,6 Гн сила тока равна 20 А. Определите энергию магнитного поля, запасенную обмоткой. Как изменится энергия магнитного поля, если сила тока в обмотке уменьшится в 2 раза?
234. Сколько витков имеет катушка индуктивностью 10-3 Гн, если при силе тока 1 А магнитный поток через поперечное сечение равен 2·10-6 Вб? Чему равна энергия магнитного поля катушки?
235. Катушка с железным сердечником сечением 20 см2 имеет индуктивность 2·10-2 Гн. Какова должна быть сила тока, чтобы индукция поля в сердечнике была 10-3 Тл, число витков равно 1000?
236. Найти индуктивность проводника, в котором равномерное изменение силы тока на 2 А в течение 0,25 с возбуждает ЭДС самоиндукции 20 мВ.
237. Какой магнитный поток пронизывал каждый виток катушки, имеющей 1000 витков, если при равномерном исчезновении магнитного поля за время t = 7 мс в катушке индуцируется ЭДС 100 В?
238. По катушке с индуктивностью 8 мкГн течет ток силой 6 А. Определите среднее значение ЭДС самоиндукции, возникающей в контуре, если сила тока изменяется практически до нуля за время t = 5 мс.
239. Соленоид имеет индуктивность 2·10-7 Гн. При какой силе тока энергия магнитного поля внутри соленоида равна 10-3 Дж?
240. В катушку с площадью поперечного сечения S = 20 см2 и числом витков N = 500 вставлен сердечник. Индуктивность катушки с сердечником 0,28 Гн при I = 5 А. Найти магнитную проницаемость сердечника.
241. Эффективная сила тока равна 7 А. Какова средняя сила тока?
242. При каком эффективном значении напряжения по обмотке катушки, имеющей омическое сопротивление 35 Ом и индуктивность 0,1 Гн, пойдет ток 3 А? Частота тока 50 Гц.
243. Какой электроемкости надо взять конденсатор, чтобы его сопротивление было таким же, как у реостата сопротивлением 500 Ом, если частота тока равна 50 Гц?
244. В катушке с омическим сопротивлением 10 Ом при частоте 50 Гц получается сдвиг фазы между напряжением и током, равный 60°. Определите индуктивность катушки.
245. На картонный цилиндр длиной 50 см и диаметром 5 см навиты 500 витков медного провода диаметром 0,5 мм. При какой частоте полное сопротивление такой катушки в 2 раза больше ее омического сопротивления?
246. К сети переменного тока (120 В; 50 Гц) присоединены параллельно конденсатор (20 мкФ) и катушка (100 Ом; 0,5 Гн). Определите силы тока в конденсаторе, катушке и общую силу тока.
247. Измерительные приборы на щитке у генератора переменного тока показывают силу тока 540 А, напряжение 235 В и мощность 108 кВт. Каков сдвиг фазы?
248. Определите потери мощности в проводке от магистрали к потребителю при следующих данных: передаваемая мощность 100 кВт; напряжение на станции 220 В; сопротивление проводки 0,01 Ом, сдвиг фазы 37°.
249. Параллельно соединенные реостат (60 Ом) и катушка (20 Ом; 0,05 Гн) присоединены к сети переменного тока (50 Гц). По катушке идет ток 4 А. Какой ток идет по реостату и чему равен полный ток, идущий от источника?
250. Мгновенное значение ЭДС синусоидального тока для фазы 30º равно 120 В. Каково амплитудное и эффективное значение ЭДС?
251. В цепь включены конденсатор емкостью 2 мкФ и катушка индуктивностью 0,05 Гн. При какой частоте тока в этой цепи будет резонанс?
252. Напряжение на концах участка цепи изменяется по закону u = U0sin ( 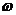 t+
t+ 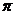 /6) В. В момент времени t = Т/12 с мгновенное значение напряжения 10 В. Определить амплитудное значение напряжения и циклическую частоту колебаний, если период колебаний 0,01 с.
/6) В. В момент времени t = Т/12 с мгновенное значение напряжения 10 В. Определить амплитудное значение напряжения и циклическую частоту колебаний, если период колебаний 0,01 с.
253. Напряжение на обкладках конденсатора изменяется с течением времени по закону u = 100sin(104 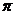 t) В. Емкость конденсатора 10-8 Ф. Найти период колебаний и индуктивность контура.
t) В. Емкость конденсатора 10-8 Ф. Найти период колебаний и индуктивность контура.
254. Каков диапазон частот собственных колебаний контура, если его индуктивность 0,1 мкГн, а емкость изменяется от 50 до 5000 пФ?
255. Какую индуктивность надо включить в колебательный контур, чтобы при емкости в 2 мкФ получить звуковую частоту 1000 Гц? Сопротивлением контура пренебречь.
256. Колебательный контур состоит из индуктивности в 10-2 Гн, емкости 0,405 мкФ и сопротивления 2 Ом. Во сколько раз уменьшится разность потенциалов на обкладках за один период?
257. Чему равно отношение энергии магнитного поля колебательного контура к энергии его электрического поля для момента времени t = Т/8 с?
258. На какой диапазон волн можно настроить контур, если его индуктивность 2 мГн, а емкость меняется от 6 пФ до 4,8 пФ?
259. Батарея, состоящая из двух конденсаторов электроемкостью по 2 мкФ каждый, разряжается через катушку индуктивностью 1 мГн и сопротивлением 50 Ом. Возникнут ли при этом колебания, если конденсаторы соединены: а) параллельно; б) последовательно?
260. Максимальное напряжение в колебательном контуре, состоящем из катушки индуктивностью 5 мкГн и конденсатора емкостью 0,013 мкФ, равно 1,2 В. Определить эффективную силу тока в контуре, максимальное значение магнитного потока, если число витков равно 28.
КОНТРОЛЬНАЯ РАБОТА № 3
