Свободные и вынужденные колебания

Среди всевозможных совершающихся вокруг нас механических движений часто встречаются повторяющиеся движения. В одних случаях каждый новый цикл очень точно повторяет предыдущий, в других различие между следующими друг за другом циклами может быть заметным. Отклонение от совершенно точного повторения очень часто настолько малы, что ими можно пренебречь и считать движение повторяющимся вполне точно, т. е. считать его периодическим.

Периодическим называют повторяющиеся движения, у которого следующий цикл в точности воспроизводит следующий другой цикл.

Продолжительность одного цикла называется периодом.

Тела, которые сами по себе могут совершать периодические движения, называются колебательными системами. Колебания, совершающиеся в этих системах без воздействия внешних сил, являются свободными.

У каждой системы, способной совершать свободные колебания, имеется устойчивое положение равновесия.

Наибольшее отклонение от положения равновесия называется амплитудой колебаний.

Колебание, которое совершает при равномерном движение точки по окружности проекция этой точки на какую-либо прямую, называется гармоническим. Кривая, изображающая гармоническое колебание, есть синусоида.

Число циклов гармонического колебания, совершаемых за 1 с называется частотой этого колебания и равна

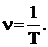(6.1)

Фазой гармонического колебания называется угол, соответствующий времени, прошедшему от какого-нибудь произвольно выбранного момента.

Наличие трения в системе приводит к затуханию колебаний.

Незатухающие свободные колебания, которые происходили бы в колебательной системе в отсутствии трения, называются собственными колебаниями.

В колебательной системе, на которую действует периодически меняющаяся сила, устанавливаются периодические движения, называющиеся вынужденными колебаниями.

Совпадение периода свободных колебаний системы с периодом внешней силы, действующей на эту систему, называется резонансом.

Амплитуда вынужденного колебания достигает наибольшего значения при резонансе.

Если сила меняется периодически, но не по гармоническому закону, то она может вызвать резонансные явления не только при совпадении её периода с периодом свободных колебаний системы, но и тогда, когда период силы в целое число раз длиннее этого периода.

Основные параметры вибрации

Под вибрациейпонимается движение точки или механической системы, при котором происходит поочередное увеличение и уменьшение во времени значений, по крайней мере, одной координаты.

Основными параметрами вибрации, происходящей по синусоидальному закону являются: амплитуда вибросмещения x_m, амплитуда виброскорости υ_m, амплитуда колебательного ускорения а_m, период колебания Т, частота ν, связанная с периодом колебаний соотношением (6.1).

Вибросмещение в случае синусоидальных колебаний определяют по формуле 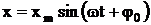, где ω – угловая частота(ω = 2πf); φ₀ – начальная фаза вибросмещения. В большинстве случаев φ₀ в задачах охраны труда значения не имеет и может не учитываться.

В общем случае физическая величина, характеризующая вибрацию, является некоторой функцией времени: υ=υ(t). Математическая теория показывает, что такой процесс можно представить в виде бесконечно длящихся синусоидальных колебаний с различными периодами и амплитудами. В случае периодического процесса частоты этих составляющих кратны основной частоте процесса.

В силу специфических свойств органов чувств определяющими являются действующие значения параметров, характеризующих вибрацию. Действующее значение виброскорости есть среднеквадратичное мгновенных значений скорости υ(t) за время усреднения Т_y:

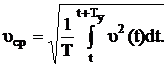(6.2)

Анализ и построение спектров параметров вибрации может производиться как в октавных, так и в третьоктавных полосах частот. В третьоктавной полосе

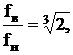(6.3)

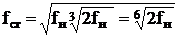. (6.4)

Так как абсолютные значения параметров, характеризующих вибрацию, изменяются в очень широких пределах, в практике используют понятие логарифмического уравнения колебаний

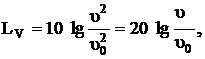(6.5)

гдеυ₀ = 5·10^-5 м/с – пороговая виброскорость.