Теплоемкостьи теплопроводность кристаллов
1. Согласно закону Дюлонга и Пти, молярная теплоемкость химически простых твердых тел при температурах, больших температуры Дебая QD:
Cm = 3R,
где R= 8,31 Дж/(моль  ) универсальная газовая постоянная.
) универсальная газовая постоянная.
Для химически сложных тел (состоящих их атомов различных химических элементов) – закон Неймана-Коппа:
Cm = 3nR,
где n – общее число частиц в химической формуле соединения.
2. Удельная теплоемкость:
- для химически простых
с = Cm/m;
- для химически сложных веществ
 .
.
3. Энергия фонона e связана с круговой частотой колебаний w соотно-шением
 ,
,
где  = h/(2p) =
= h/(2p) =  .
.
4. Квазиимпульс фонона
p = h /l,
где h = 
5. Скорость 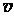 фонона (скорость звуковых волн в кристалле в пренебрежении дисперсией)
фонона (скорость звуковых волн в кристалле в пренебрежении дисперсией)
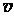 = wl/(2p).
= wl/(2p).
6. Частота Дебая (максимальная частота колебаний кристаллической решетки)
wD = 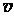 (6p2n)1/3 ,
(6p2n)1/3 ,
где n = N/V –концентрация атомов в кристалле,
n= NAr/m,
где r - плотность кристалла;m - молярная масса.
7. Температура Дебая:
 ,
,
где k – постоянная Больцмана, k =  Дж/K.
Дж/K.
8. Поток тепловой энергии Q, проходящий через поперечное сечениеS стержня в единицу времени
Q = -l(dT/dx)S,
где l - теплопроводность;dT/dx – градиент температуры.
l =  l
l  /3,
/3,
где  –групповая скорость фононов;l – средняя длина свободного пробега фононов между двумя последовательными столкновениями;
–групповая скорость фононов;l – средняя длина свободного пробега фононов между двумя последовательными столкновениями;  –теплоемкость единицы объема.
–теплоемкость единицы объема.
9. Молярная теплоемкость кристаллической решетки при температуре T<<  :
:
Cm = 12p4R (T/  )3/5 = 234R(T/
)3/5 = 234R(T/  )3.
)3.
Примеры решения задач
Задача 1
Вычислить по классической теории теплоемкостькристалла бромида алюминия (AlBr3) объемом 200см3. Плотность кристалла бромида алюминия равна 3,01 г/см3. Условие T>  считать выполненным.
считать выполненным.
Дано: V =  м3 м3  | Решение: Химическая формула соединения AlBr3 содержит четыре атома (n=4). Поэтому, согласно закону Неймана-Коппа, молярная теплоемкость кристалла: |
| С = ? |
Сm = n3R = 99,7 Дж/моль К.
Теплоемкость всего кристалла
C= Cmm/m = CmrV/m = 12RrV/m. (1)
По таблице Менделеева находим: A(Al) = 27, A(Br) = 80, следовательно M(AlBr3) =267, а m = 0,267 кг/моль. Подставляя в формулу (1) числа, получаем
С = 225 Дж/K.
Задача 2
Вычислить длину волны фононов в свинце, соответствующую частоте w = 0,1wD, если плотность свинца 11,3 г/cм3, а молярная масса 207 г/моль.
Дано: r =  кг/м3 m = кг/м3 m =  кг/моль w= 0,1 wD кг/моль w= 0,1 wD | Решение: Частота Дебая (максимальная частота колебаний кристаллической решетки) определяется выражением: wD = 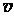 (6p2n)1/3, (1) (6p2n)1/3, (1) |
| lF = ? |
где 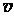 – средняя скорость распространения колебаний(скорость звука) в кристалле;n – концентрация атомов в кристалле,
– средняя скорость распространения колебаний(скорость звука) в кристалле;n – концентрация атомов в кристалле,
n= NAr/m. (2)
В пренебрежении дисперсией звука в кристалле:
lF = 2p 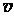 /w,
/w,
или, согласно условию задачи,
lF = 20p 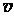 /wD.
/wD.
Окончательно, пользуясь формулами (1) и (2), получаем
lF = 20p(6p2NAr/m)-1/3 (3)
Подставляя в формулу (3) NA =  1023и числовые данные из условия задачи, будем иметь: lF =
1023и числовые данные из условия задачи, будем иметь: lF = 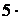 10-9 м.
10-9 м.
Задача 3
Определить температуру Дебая для серебра, если известно, что для нагревания серебра массой 15 г от температуры 5 К до температуры 10 К надо затратить количество тепла  10-2Дж. Условие T<<
10-2Дж. Условие T<<  считать выполненным.
считать выполненным.
| Дано: m= 0,015 кг Q = 6,8 10-2 Дж Т1 = 5 К Т2 = 10 К | Решение: Так как по условию задачи T<<Q, то можно воспользоваться формулой Дебая: Cm = (12/5)p4R(T/  )3 = 234R(T/ )3 = 234R(T/  )3 (1) Теплоемкость С тела связана с молярной теплоемкостью Cm соотношением: )3 (1) Теплоемкость С тела связана с молярной теплоемкостью Cm соотношением: |
 =? =? |
С = Cmm/m (2)
Подставляя (2) в (1) и интегрируя по температуре от Т1 до Т2, получаем
Q = (3p4mR/5m  3) [T24 – T14]. (3)
3) [T24 – T14]. (3)
Выразим из формулы (3) температуру Дебая:
 = ((3p4mR/5mQ)[T24 – T14])1/3. (4)
= ((3p4mR/5mQ)[T24 – T14])1/3. (4)
Произведем вычисления по формуле (4), учтя, что у серебра молярная масса равна m = 0,108 кг/моль:  = 210 K.
= 210 K.
Электронный газ в металлах
1. Концентрация электронов dn(e), энергия которых заключена в интервале значений от Е до Е + dЕ:
dn(Е) = (2m*)3/2 (2p2  )-1Е1/2 (
)-1Е1/2 (  +1) -1,
+1) -1,
где m*и Е – эффективная масса и энергия электрона;m =EF– энергия Ферми.
2. При Т = 0
EF = (  /2m*) (3p2n) 2/3.
/2m*) (3p2n) 2/3.
3. Средняя энергия электронов при Т = 0:
<E> = 3/5 
4. Температура Ферми
TF =  .
.
5. Температура вырождения
Тв = 4/(9p) 1/3TF = 1,313TF.
Примеры решения задач
Задача 1
Определить температуру вырождения для калия, если считать, что на каждый атом приходится по одному свободному электрону. Плотность калия r = 860 кг/м3.
| Дано: r(K) = 860 кг/м3 | Решение: Температура вырождения ТB согласно квантовой теории электронов в металле определяется выражением: ТB = h2n2/3/(2pkm), (1) |
| ТB = ? |
где h= 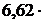 10-34Дж·с – постоянная Планка; k = 1,38 10-23Дж/К – постоянная Больцмана;m=
10-34Дж·с – постоянная Планка; k = 1,38 10-23Дж/К – постоянная Больцмана;m=  10-31кг – масса электрона;n – концентрация квазисвободных электронов в металле. Согласно условию,nравно концентрации Nатомов, которая определяется выражением:
10-31кг – масса электрона;n – концентрация квазисвободных электронов в металле. Согласно условию,nравно концентрации Nатомов, которая определяется выражением:
N = NAr/m, (2)
где NA –число Авогадро;r - плотность кристалла;m - молярная масса калия. По таблице Менделеева: m =  10-3 кг/моль.
10-3 кг/моль.
Полагая n = Nи подставляя выражение (2) в формулу (1) с учетом приведенных выше числовых данных окончательно получаем
ТВ = 3,12 104 К.
