Пространственная решетка кристалла
1. Координаты любого узла решетки записываются в виде
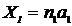 ;
; 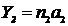 ;
; 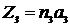 и обозначаются: [[n1n2n3]], где ai– основные периоды решетки;ni– целые числа, называемые индексами узла и обозначающие число периодов решетки, соответствующих данному узлу,
и обозначаются: [[n1n2n3]], где ai– основные периоды решетки;ni– целые числа, называемые индексами узла и обозначающие число периодов решетки, соответствующих данному узлу, 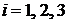 .
.
Для описания направления в кристалле выбирают прямую, проходящую через начало координат. Ее направление однозначно определяется индексаминаправления[n1n2n3], где ni – индексы ближайшего к началу координат узла решетки.
2. Период идентичности вдоль прямой, заданной индексами [n1n2n3], в кубической решетке выражается соотношением
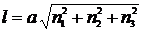 ,
,
где а – параметр решетки.
3. Кристаллографическиеплоскости определяются тремя взаимно простыми целыми числами (hkl), называемыми индексамиМиллера. Они определяют систему бесконечного числа параллельных между собой плоскостей, каждая из которых характеризуется определенным значением числа
q= 0, +1, +2,…
Таким образом, кристаллографическая плоскость однозначно задается совокупностью чисел {(hkl),q}. Для отрицательных индексов над (или под) буквой ставится знак минус, например h. Индексы [[n1n2n3]] любого узла, лежащего в данной плоскости, удовлетворяют соотношению:
n1h + n2k + n3l = q.
При q = 0 плоскость проходит через начало координат.
Если плоскость параллельна какой-либо оси координат, то соответствую-щий индекс Миллера равен нулю. Так, плоскость (110) параллельна оси z, а плоскость (100) параллельна плоскости (yz).
4. Расстояние Dплоскости от начала координат определяется числом q
D = q/b0,
где
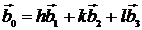 ,
,
где 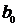 – вектор обратной решетки;
– вектор обратной решетки; 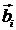 (i = 1,2,3) – базисные векторы обратной решетки
(i = 1,2,3) – базисные векторы обратной решетки
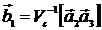 ,
, 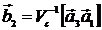 ,
, 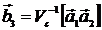 ;
;
Vc– объем элементарной ячейки кристалла.
Из выражения 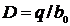 следует, что расстояние dмежду соседними плоскостями (Dq= 1) с индексами (hkl) равно:
следует, что расстояние dмежду соседними плоскостями (Dq= 1) с индексами (hkl) равно:
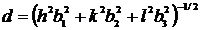 .
.
5. Кристаллические плоскости отсекают на осях координат отрезки, равные
xq = а1q/h, yq = a2q/k, zq = a3q/l
Очевидно, что если q/h, q/kиq/l – целые числа, то плоскость пересекает соответствующую координатную ось в узловой точке.
6. Молярный объем кристалла
Vm = m/r,
где m –молярная масса;r – плотность кристалла.
7. Объем элементарной ячейки в случае кубической сингонии
Vэл = а3,
где а – параметр решетки.
8. Число элементарных ячеек в одном моле кристалла
Zm = Vm/Vэл
Если кристалл состоит из одинаковых атомов, то
Zm = NA/n,
где NA – число Авогадро;n – число одинаковых атомов, приходящихся на элементарную ячейку.
9. Число элементарных ячеек в единице объема кристалла
Z=Zm/Vm.
Если кристалл состоит из одинаковых атомов, то
Z = rNA/(nm)
10. Параметр решетки, состоящей из одинаковых атомов
a = (nm/rNA)1/3
Расстояние между соседними атомами в кубической решетке:
а) в простой d =a;
б) в гранецентрированной 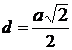 ;
;
в) в объемноцентрированной 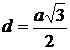 .
.
11. Число одинаковых атомов, приходящихся на элементарную ячейку:
а) простая кубическая решетка n= 1;
б) гранецентрированная кубическая решетка n = 4;
в) объемноцентрированная кубическая решетка n = 2.
Примеры решения задач
Задача 1
Определить параметр решетки и плотность кристалла кальция, если расстояние между ближайшими соседними атомами равно 0,393 нм. Решетка кубическая, гранецентрированная.
Дано: NA = 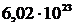 моль-1 m = моль-1 m = 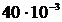 кг/моль d = кг/моль d = 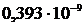 м n = 4 м n = 4 | Решение: Параметр решеткиа и расстояние d между двумя ближайшими соседними атомами связаны соотношением: 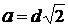 . . |
| a =? r = ? |
Подставляя в это выражение числовые значения, получим:
а = 5,56 10-10 м.
Плотность кристалла
r = mn/(NAa3) = 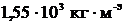 .
.
Задача 2
Вычислить период идентичностиlвдоль прямой [2 3 1] в решётке NaCl, если плотность кристалла равна 2,17 г/см3. Решётка гранецентрированная кубическая.
Дано: n1 = 2, n2 = 3, n3 = 1 r= 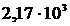 кг/м3 кг/м3 | Решение: Постоянная решетки кристалла NaClравна a = (nm/(rNA))1/3 (1) Число Авогадро NA =6,02 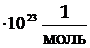 . . |
| l = ? |
Для гранецентрированной решетки число узлов в элементарной ячейке 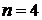 . Пользуясь таблицей Менделеева, находим: A(Na) = 23, A(Cl)=35. Следовательно, M(NaCl)=58, откуда молярная масса NACl:
. Пользуясь таблицей Менделеева, находим: A(Na) = 23, A(Cl)=35. Следовательно, M(NaCl)=58, откуда молярная масса NACl:
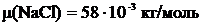 .
.
Подставляя числа в формулу (1), получаем
а = 5,62 10-10 м.
Период идентичности кристалла вдоль прямой [231]
l= a(n12 + n22 + n32)1/2 = 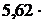 10-10 (4 + 9 + 1)1/2 = 13,3 10-10м
10-10 (4 + 9 + 1)1/2 = 13,3 10-10м
Задача 3
Написать индексы Миллера для плоскости, проходящей через узлы с индексами: [[010]], [[122]], [[132]]. Найти отрезки, отсекаемые этими плоскостями на осях координат.
| Дано: Индексы узлов: [[010]], [[122]], [[132]]. | Решение: Для любого узла с индексами [[n1n2n3]], лежащего в данной плоскости, индексы Миллера (hkl) удовлетворяют соотношению: n1h+ n2k + n3l = q, (1) |
| (hkl) =?, xq=?, yq=?, zq=? |
где h,k,l,q – целые числа. Подставляя в уравнение (1) последовательно индексы всех трех узлов, получаем систему уравнений:
k=q
h + k – 2l = q
h + 3k + 2l =q
Решая эту систему в целых числах, получаем: h= -6, k=4, l =-1; q=4, т.е. данная плоскость задается индексами: {(641);4}. Она отсекает на осях координат отрезки, равные
x0 = a1q/h= -2/3 a1; y0 = a2q/k = a2; z0 = -4a3,
где аi(i = 1,2,3) – основные периоды решетки. Плоскость пересекает оси у и zв узловых точках.
