Измерение радиуса кривизны линзы и длин световых волн при помощи интерференционных колец ньютона

Цель работы: изучить явление интерференции и ознакомиться с одним из частных случаев интерференции кольцами Ньютона и с их помощью определить радиус кривизны линзы и длину волны света.

Приборы и принадлежности: микроскоп, окулярный микрометр, плосковыпуклая линза большого радиуса кривизны, плоскопараллельная пластинка, источник света (лампа накаливания, неоновая лампочка), набор светофильтров.

Введение

Кольца Ньютона являются частным случаем интерференции световых волн, возникающей при освещении плосковыпуклой линзы с большим радиусом кривизны, расположенной на плоской зеркальной поверхности. Когерентные интерферирующие волны возникают при отражении параллельных лучей, падающих перпендикулярно на плоскую поверхность линзы от границы раздела линза— воздух и воздух — плоская поверхность (см. рис. 1. Для простоты показан один луч, падающий на плоскую поверхность линзы).

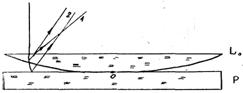
Рисунок 1

Линза расположена выпуклой частью на плоской пластинке. Между линзой и пластинкой имеется зазор, заполненный воздухом или другим веществом. В точке О толщина воздушной прослойки в зазоре значительно меньше длины волны света, и в отраженном свете в центральной точке всегда наблюдается темнота. Здесь происходит сложение двух волн в противоположных фазах, т.к. первое отражение линза—воздух происходит от оптически менее плотной среды и отраженный луч не меняет фазу, а в случае отражения воздух—стекло (от нижней грани воздушной прослойки) имеет место смена фазы отраженного луча на π, а это равносильно изменению разности хода волн на λ/2, т.к. происходит отражение от оптически более плотной среды. На некотором удалении от точки О луч света проходит путь, где толщина воздушного зазора равна d. Величина d будет тем больше, чем дальше находится точка падения луча от точки О. Радиус линзы значительно больше толщины зазора, поэтому можно считать, что отраженные лучи 1 и 2 будут совпадать по направлению. Там, где толщина воздушного зазора d=λ/4, геометрическая разность хода этих лучей будет равна λ/2, т. к. луч 2 проходит этот зазор дважды. А вследствие перемены фазы этим лучом при отражении от оптически более плотной среды, оптическая разность хода этих двух лучей будет равна λ. Для этих точек будет наблюдаться максимум интерференции при сложении этих лучей. Места одинаковой толщины воздушного зазора расположены вокруг точки О концентрическими окружностями. Слой толщиной d=λ/4 образует первое светлое кольцо, следующее за центральным темным пятном. После несложных математических рассуждений условие максимума интерференции отраженных лучей будет записано в виде:

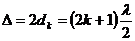(1)

Условие минимума интерференции в этом случае имеет вид:

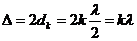(2)

где Δ .— оптическая разность хода интерферирующих лучей,

d_k — толщина воздушной прослойки,

λ — длина волны света, падающего на линзу,

к — порядковый номер, к = 0, 1, 2...

Так как измерить толщину воздушного зазора между линзой и плоским зеркалом трудно, ее обычно исключают, выражая через радиус соответствующих темных колец — r_k.

Связь между толщиной воздушной прослойки d_k, радиусом темного кольца г_k и радиусом кривизны линзы R можно легко получить, вспомнив известную теорему из геометрии (рис. 2).

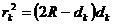(3)

Раскрывая скобки и учитывая, что d_k<<R, то d_k² можно пренебречь, тогда

r_k²=2Rd_k (4)

Подставив в уравнение (4) значение d_k из уравнения (2), получаем уравнение, связывающее радиусы темных колец с радиусом кривизны линзы и длиной волны света

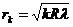(5)

для светлых колец 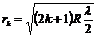(6)

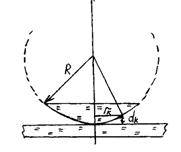
Рисунок 2

Если наблюдение проводить в проходящем свете, расположение темных и светлых колец будет в обратном порядке, т. е. в точке О будет светлое пятно, за ним следует темное и т. д. Уравнение (5) будет давать значение радиусов светлых колец, а (6) - темных.

В данной работе уравнение (5) является расчетным.Его можно использовать либо для определения R — радиуса кривизны линзы, если осветить установку светом с известной длиной волны, а экспериментально определять r_k и k; либо для определения λ — длины волны света, если используется линза с известным радиусом кривизны, также измеряя r_k и k.

На практике измеряют радиус не одного кольца, а нескольких и, записывая уравнение (5), дважды для колец с порядковым номером “m” и “n”, получают уравнение для расчета λ и R.

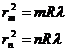(7)

Вычитая из первого уравнения второе, получаем

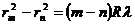(8)

Из уравнения (8) можно получить уравнение

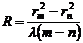(9)

для расчета радиуса кривизны.

Описание установки

Измерение радиусов колец Ньютона в данной работе осуществляется с помощью микроскопа МБС, в одну из окулярных трубок которого установлен источник света и светофильтр, а в другую трубку вставлен окулярный микрометр. Это дает возможность наблюдать кольца Ньютона в отраженном свете при нормальном падении световой волны на линзу, так как в оптической головке микроскопа установлены специальные призмы (призмы Шмидта), позволяющие направлять луч света на объект и от объекта под прямым углом, а окулярные трубки разворачивать по глазу наблюдателя.

На предметный столик микроскопа кладется приспособление, позволяющее получать интерференционную картину. Оно состоит из плотно прижатой выпуклой стороной плосковыпуклой линзы и плоскопараллельной пластинки.

Измерение радиусов колец Ньютона осуществляется с помощью окулярного микрометра (рис. 3).

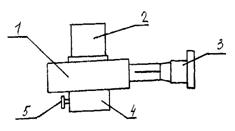
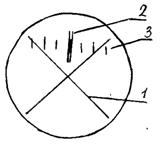
Рисунок 3 Рисунок4

Окулярный микрометр состоит из корпуса 1 с хомутиком 4, который одевается на тубус микроскопа и закрепляется винтом 5 окуляра 2 с диоптрийным механизмом. Вращением окуляра устанавливают его на резкое изображение перекрестия 1(рис. 4).

В фокальной плоскости окуляра расположены: неподвижная шкала 3 с делениями от 0 до 8 (рис.4), подвижные перекрестие 1 и индекс 2 в виде биштриха. При вращении микрометрического винта 3 (рис. 3) перекрестие 1 и биштрих 2 (рис. 4) перемещаются в поле зрения окуляра 2 относительно неподвижной шкалы 3. Шаг винта равен 1 мм. При повороте винта 3 за накатанную часть барабана (рис. 3) на один оборот биштрих и перекрестие в поле зрения окуляра (рис. 4) переместятся на одно деление шкалы.

Следовательно, неподвижная шкала в поле зрения служит для отсчета полных оборотов барабана винта.

Барабан 3 по окружности разделен на 100 частей. Поворот барабана на одно деление соответствует перемещению перекрестия на 0,01 делений неподвижной шкалы.

Полный отсчет по шкалам окулярного микрометра складывается из отсчета по неподвижной шкале и отсчета по барабану винта. Отсчет по неподвижной шкале в поле зрения определяется положением биштриха. Отсчет по барабану микрометрического винта производится как и по обычному микрометру, т. е. определяется деление шкалы, которое находится против индекса, нанесенного на неподвижном цилиндре барабана.

Измерение диаметра колец сводится к определению координат колец по шкале окулярного микрометра. Вращая барабан микрометрического винта, устанавливаем перекрестие на темное кольцо (вначале на правый край первого, затем второго, третьего и т. д., каждый раз производя отсчет по шкале и барабану, как сказано выше). Затем так же отсчитываем координаты ряда последовательных колец слева.

Вычитая из большей координаты меньшую для одного и того же кольца, получаем диаметр соответствующего кольца в условных единицах. Разделив диаметр на два, получаем значение радиуса. Умножив полученное значение радиуса кольца на переводной коэффициент, приведенный в таблице 3.1, получим истинный размер кольца в миллиметрах.

Порядок выполнения работы

1. Включите осветитель микроскопа.

2. На барабане увеличения микроскопа, где собраны призмы Шмидта, установите “2”.

3. Вращением окуляра за накатанную часть установите резкое изображение перекрестия в поле зрения окулярного микрометра.

4. Получите четкое изображение колец Ньютона в поле зрения окулярного микрометра.

5. Запишите в заранее подготовленную таблицу координаты 5—6 темных колец, считая от центрального темного пятна сначала справа, затем слева.

6. Найдите разность координат справа и слева для одного и того же кольца.

7. Определите истинный радиус колец, умножая на переводной коэффициент из таблицы 3.1 половину диаметра кольца, рассчитанного в пункте 6.

8. Зная длину волны зеленого цвета (мы пользуемся зеленым светофильтром λ=4,86·10^-7м) по уравнению (9) рассчитайте радиус кривизны линзы.

9. Все измерения занесите в таблицу 2.

Таблица 1

Увеличение микроскопа по барабану	Одно деление шкалы окулярного микрометра соответствует истинной длине
0,1 мм	1 мм
0,6	0,17	1,7
	0,1
	0,05	0,5
	0,025	0,25
	0,014	0,14

Таблица 2. Измерение радиуса кривизны линзы

№ колец	Координаты колец	Диаметр кольца a-b	Радиус кольца (a-b)/2	Истинный радиус rk	Радиус кривизны R	Абс. погрешн. ΔR
cправа a	cлева b

Контрольные вопросы

1. Что такое интерференция света?

2. Каковы условия наблюдения интерференции света?

3. Чем отличаются интерференционные картины принаблюдении колец Ньютона в отраженном и проходящем свете?

4. Почему при удалении от центра линзы, расстояние между кольцами Ньютона уменьшается?

5. Когда и почему кольца Ньютона оказываются окрашенными?

6. Где применяется явление интерференции?

7. Почему нельзя наблюдать интерференцию света в обычныхусловиях?

8. Что такое оптическая длина пути?

9. Напишите уравнение световой волны.

10. Какое свойство света проявляется в явлении интерференции?

11. Какие способы создания когерентных волн вы знаете?

ЛАБОРАТОРНАЯ РАБОТА №22