Определение коэффициента поверхностного натяжения методом отрыва капель

Установка для определения коэффициентов поверхностного натяжения жидкостей данным методом представлена четырьмя бюретками А.В.С.Д, закрепленными на стенде (рис.3) Истечение жидкости из бюретки регулируется зажимом К.

Метод основан на сравнении силы поверхностного натяжения, удерживающей каплю от падения, с силой тяжести под действием которой отрывается капля. Капля отрывается тогда, когда ее вес Р будет немного больше или в предельном случае, равен силе поверхностного натяжения F, удерживающей каплю от падения. Таким образом, в момент отрыва капли получаем условие: Р=F (5)

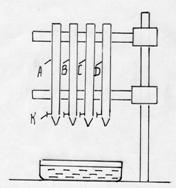
Рисунок 3.

По уравнению (4) полагая l=2pR – дина окружности шейки бюретки, получим

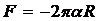(6)

с учетом условия (5) получим

(7)

из уравнения (7) определяем a:

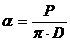(8)

где Р – вес одной капли,

D – диаметр шейки капли.

Рабочая формула имеет вид:

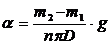(9)

где m₁ – масса пустого стакана,

m₂ – масса стакана с некоторым количеством капель,

g – ускорение силы тяжести, g=9,8 м/с²

D – внешний диаметр капилляра (смотрите на приборе),

n – число капель в сосуде.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Взвесьте пустой стакан. Запишите его массу m₁.

2. Отсчитайте «n» капель, вытекающих из бюретки.

3. Взвесьте стакан с «n» каплями. Запишите массу m₂.

4. Определите по уравнению (9) коэффициент поверхностного натяжения исследуемой жидкости.

5. Проделайте опыты со всеми предлагаемыми жидкостями.

6. Данные занесите в таблицу 1.

7.

Таблица 1. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ МЕТОДОМ ОТРЫВА КАПЕЛЬ

Исследуемая жидкость	m1	n	m2	m=m2-m1	D	a	Da
Вода

ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ

1. Проделать измерения с мыльным раствором.

2. Сделать выводы и указать область использования жидкостей с низким коэффициентом поверхностного натяжения.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Каков физический смысл коэффициента поверхностного натяжения? Каковы единицы измерения? Отчего зависит a?

2. Объясните явление смачивания и не смачивания. Мениск.

3. Что представляет собой явление капиллярности?

4. Выведите уравнение для высоты поднятия жидкости в капиллярах.

5. Запишите уравнение для добавочного давления жидкости над искривленной поверхностью (Уравнение Лапласа).

6. Как зависит a от температуры.

7. Опешите характер теплового движения молекул в жидкости.

8. Когда величина коэффициента поверхностного натяжения равна 0?

9. Какую работу может выполнить поверхностная пленка, сокращаясь на 1 см²?

ЛАБОРАТОРНАЯ РАБОТА№ 9

ОПРЕДЕЛЕНИЕ ИЗМЕНЕНИЯ ЭНТРОПИИ

Цель работы: опытным путем установить зависимость изменения энтропии от тёплоемкости тел при выравнивании температур тел в изолированной адиабатической термодинамической системе.

Приборы и принадлежности: калориметр, термометр, водомерный стакан, нагреватель, набор из шести: испытуемых тел: четыре железных с массами 50,100, 150, 200 г, латунное и алюминиевое с массами 50 г каждое.

Теоретическое введение

Так же как и внутренняя энергия, энтропия является функцией состояния термодинамической системы. Если термодинамическая система получает в обратимом процессе количество теплоты dQ при температуре Т, то отношение 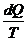определяет изменение энтропии системы, т.е.

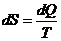
и. для обратимого процесса является полным дифференциалом. На практике обычно интересуются только изменением энтропии, а не ее абсолютным значением.

Изменение энтропии системы можно найти, используя второе начало термодинамики

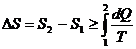(1)

где интеграл берется по пути термодинамического процесса между состояниями 1 и 2, где S₁ и S₂ - значения энтропии в этих состояниях. Знак равенства соответствует обратимому процессу, а знак неравенства - необратимому.

Второе начало термодинамики (1) утверждает, что при обратимом процессе изменение энтропии системы равно интегралу от 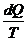между состояниями 1 и 2 по обратимому пути и больше этого интеграла по пути необратимому, т.е. в этом случае интеграл от 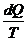не выражает изменение энтропии, а меньше его.

Представляет интерес изучение изменения энтропии в изолированной адиабатической системе.

Изменение энтропии в изолированной адиабатической системе при квазистатическом (обратимом) процессе равно нулю, так как dQ=0, т.е.

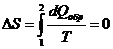
В случае необратимых процессов в изолированной адиабатической системе dQ также равно нулю, но изменение энтропии в такой системе уже нулю не равно и по формуле (1) для обратимых процессов не может быть вычислено. Это вычисление можно сделать, если учесть, что энтропия есть функция состояния системы и ее применение не зависит от характера пути процесса в системе, т.е. обратимого или необратимого. В этом случае для вычисления изменения энтропии можно воспользоваться любым квазистатическим (обратимым) процессом, переводящим систему из состояния 1 в 2, т.е.

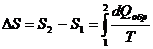(2)

В случае выравнивания температуры от Т1 до Т2 твердых и жидких тел в изолированной адиабатической системе этот реальный процесс можно заменить изобарическим квазистатическим (обратимым) переходом теплоты между телами. При изобарическом процессе

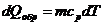
где т - масса тела; C_p — удельная теплоемкости тела при постоянном давлении. Для характеристики теплоемкости тел используется также и удельная теплоемкость при постоянном объеме — С_v. У жидких и твердых тел разница между Ср и Сv сравнительно мала, так что можно положить С_р С_v и говорить просто об удельной теплоемкости жидких и твердых тел С Нужно помнить, что удельная теплоемкость вещества С зависит от температуры, т.е. С = С(Т). Тогда изменение энтропии в этом процессе можно определить

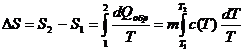(3)

В нашем случае вместо С(Т) будем использовать среднее значение удельной теплоемкости С в интервале температур от Т₁ до Т₂ и считать для этого температурного интервала среднее значение удельной теплоемкости С величиной постоянной, тогда изменение энтропии будем вычислять по формуле:

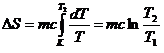(4)

В силу того, что энтропия аддитивна, полное изменение энтропии термодинамической системы можно найти, если просуммировать изменения энтропии всех отдельных тел, входящих в состав этой системы, т.е.

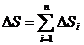(5)

где ∆S - - изменение энтропии всей системы; п - число тел системы; ∆S₁ - изменение энтропии одного из тел термодинамической системы.

Согласно первому началу термодинамики

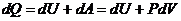
сообщаемое термодинамической системе тепло dQ идет на изменение внутренней энергии системы dU и совершение системой работы dA=PdVнад внешними телами. В случае твердого и жидкого тел все сообщаемое тепло идет на изменение внутренней энергии, а так как объемы этих тел при нагревании почти не изменяются, то работой расширения dA=PdV можно пренебречь, т.е., чем больше изменение энтропии в адиабатно-изолированной системе, тем большее количество тепла необратимо переходит во внутреннюю энергию системы. Поэтому необратимые потери тепла, связанные с реальными необратимыми термодинамическими процессами в адиабатно-изолировашых системах, принято оценивать по изменению энтропии.

Если в калориметр, содержащий определенное количество воды при заданной температуре, опустить нагретое тело, то произойдет теплообмен и установится общая температура. Сам калориметр помещен во внешний стакан, в результате чего система становится почти адиабатно-изолированной.

Термодинамическому равновесию адиабатической системы соответствует состояние с максимумом энтропии, при этом температура вест частей системы в состоянии равновесия одинакова.

Изменение энтропии такой системы при выравнивании температуры погруженного тела и воды можно рассчитать по формулам (4) и (5).В состав исследуемой системы входят: испытуемое тело массой m_Tс удельной теплоемкостью С_T и начальной температурой Т₀, вода калориметра массой m_Bудельной теплоемкостью С_B и начальной температурой Т₀ . После окончания процесса теплообмена установится температура Т.

При выравнивании температуры энтропия каждого из тел изменяется:

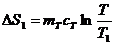(тело),

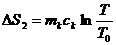(калориметр),

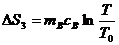(вода в калориметре).

Учитывая аддитивность энтропии (5),можно записать

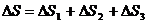
Подставляя значения ∆S₁, ∆S₂, ∆S₃ получим расчетную формулу изменения энтропии всей системы

(6)

В данной работе

m_B=0,2 кГ; C_B=4,18_*103 Дж/кГ_*град (при t=20°C)

C_T (железо)=460,5 Дж/кГ_*град;

С_Т (латунь)=376,7 Дж/кГ_*град;

С_Т (алюминий)=879,1 Дж/кГ_*град.

В работе предлагается рассчитать изменение энтропии шести нагретых тел при опускании в калориметр с водой, температура и масса которой одинаковы в каждом эксперименте.

Порядок выполнения работы

1. Опустить в нагреватель испытуемое тело. Включить нагреватель.

2. Пока тело нагревается до температуры Т₁ кипения воды, наполнить водой водомерный стакан (200 см) и выпить ее в стакан калориметра. По термометру определить начальную температуру Товоды и калориметра.

3. После того как вода в нагревателе будет кипеть не менее 5мин, отключить нагреватель, перенести за нить исследуемое тело в калориметр и быстро закрыть его.

4. По термометру калориметра следить за ростом температуры воды и записать в таблицу ее максимальное значение Т.

5. Выпить воду из стакана калориметра и охладить его под струёй воды.

6. Действия, перечисленные в пп. 1-5, повторить с каждым из тел.

7. Определить теплоемкость С каждого из тел и результаты занести в табл. 1.

8. По формуле (6) найти изменение энтропии ∆S для каждого из тел и записать в табл. 1. Вычислить погрешность метода измерения для самого легкого тела (максимальную погрешность).

9. По данным табл. 1 построить график зависимости ∆S=ƒ(C)

Таблица 1.

Исследуемое тело	0,05 кг	0,1 кг	0,15 кг	0,2 кг	0,05 кг	0,05 кг
T(K)
C(Дж/К)
∆S(Дж/К)

Контрольные вопросы:

1. Что такое обратимые и необратимые процессы?

2. Охарактеризуйте энтропию и ее изменение.

3. Что такое термодинамическая вероятность состояния (статический вес)?

4. Статический смысл изменения энтропии.

5. Первый закон термодинамики.

6. Вывод рабочей формулы (6) данной работы.

7. Второй закон термодинамики и его статический смысл.

ЛАБОРАТОРНАЯ РАБОТА №10