Введение в теорию измерений физических величин

ЗАДАЧА ИЗМЕРЕНИЙ. ОСНОВНЫЕ ПОНЯТИЯ И ИХ ОПРЕДЕЛЕНИЯ

Физика – одна из естественных наук, цель которой – познание природы.

При проведении эксперимента требуется не только наблюдать явления, но и измерять, чтобы установить количественную связь между величинами и выразить ее математическим уравнением. В задачу измерения входит не только нахождение значения измеряемой величины, но также и оценка допущенной при измерении погрешности. Таким образом, измерить – значит найти Х ± DХ

Недостаточное внимание к точности измерения и к методу может привести к очень существенным погрешностям, а иногда к прямым ошибкам в экспериментальных результатах.

Для того, чтобы правильно измерять, необходимо руководствоваться определенными правилами и приемами при проведении самих измерений и обработке полученных результатов. Хотя рекомендации в этом отношении не могут быть универсальными, но многие общие приемы и правила достаточно хорошо разработаны и, прежде чем приступить к работе в лаборатории, необходимо с ними познакомиться и усвоить.

Современный ГОСТ 16263-70 дает конкретные определения основных метрологических понятий:

- измерением называется операция нахождения значений физической величины с помощью технических средств;

- истинным значением физической величины называют значение физической величины, которое идеальным образом отражает в качественном и количественном отношениях соответствующие свойства объекта.

- погрешностью измерения называют отклонение результатов измерения от истинного значения измеряемой величины.

Так как истинное значение неизвестно, то можно найти лишь приближенную оценку погрешности, используя действительное значение физической величины.

Действительным значением физической величины называют такое ее значение, которое находят экспериментальным путем и оно настолько приближается к истинному значению, что для данной цели может быть использовано вместо него.

Нахождение действительного значения измеряемой величины представляет задачу метрологии, требует определенных средств измерения и специальных методик.

В практике лабораторных работ в курсе общей физики с учетом выводов теории вероятностей и математической статистики за действительное значение измеряемой величины можно принимать среднее арифметическое значение измеряемой величины, полученное из n измерений, т.е.

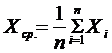(1)

где n – число измерений;

Х_i – результат отдельного измерения с порядковым номером i, i=1,2,3..

S - знак суммы.

С учетом сказанного и в соответствии с ГОСТом под оценкой абсолютной погрешности измерения понимают разность между значением измерения – X_i и действительным значением измеряемой величины – X_g, выраженную в единицах измеряемой величины и взятую со знаком (+) или (-), т.е.

(2)

где DХ – абсолютная погрешность измерения;

Х_i – измеренное значение величины;

Х_g – действительное значение величины.

Но абсолютная погрешность может дать оценку качества измерения лишь при сопоставлении ее с результатом измерения. Поэтому результат измерения обычно оценивают величиной относительной погрешности: - относительной погрешностью измерения называют отношение абсолютной погрешности к действительному значению измеряемой величины, т.е.

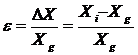(3)

Относительная погрешность – безразмерная величина, но обычно ее выражают в процентах.

КЛАССИФИКАЦИЯ ИЗМЕРЕНИЙ.

По способу получения измеряемой величины измерения бывают прямыми и косвенными

а) Прямые измерения это такие, при которых искомая величина получается непосредственно в процессе измерения.

Примеры: определение длины стола с помощью метра, измерение напряжения в сети вольтметром, измерение сопротивления мостом постоянного тока и пр.

б) Косвенные измерения это такие, при которых измеряется не сама искомая величина, а ряд величин, связанных с ней функциональной зависимостью.

(считаем, что расчеты проводим для цепи постоянного тока).

КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ

По причинам, вызывающим погрешности, они делятся на:

1) систематические,

2) случайные,

3) промахи.

Систематические погрешности обусловлены действующими причинами. Они вызываются неточностью прибора, несовершенством метода измерений и т.п. При повторении эксперимента их величина и знак сохраняются. Увеличение числа измерений не устраняет систематических погрешностей.

Способ борьбы с систематическими погрешностями является отыскание поправок к измерительным приборам.

Случайные погрешности – результат одновременного действия различных возмущающих факторов, не связанных между собой. Случайные погрешности неизбежны, и тем заметнее, чем чувствительнее прибор. При отсутствии систематических погрешностей они служат причиной разброса повторных измерений относительно истинного значения измеряемой величины.

Случайные погрешности исключить нельзя, но они могут быть вычислены с помощью статических методов. При обработке результатов измерений пользуются тремя аксиомами:

1) За наиболее вероятный результат измерений или за значение измеряемой величины принимают среднее арифметическое n измерений.

2) Вероятность появления малых погрешностей больше, чем вероятность появления больших погрешностей.

3) Погрешности положительные встречаются также часто, как погрешности отрицательные, т.е. закон их распределения симметричный.

Эти аксиомы приводят к нормальному закону распределения – закону Гаусса.

где d - среднеквадратичная погрешность измерений, которая находится по формуле:

(4)

DХ_i – абсолютная погрешность i –го измерения.

Погрешности косвенных измерений

Пусть искомая величина f определяется из прямых измерений величины х, причем f=f(х). Это значит, что величина f получается в результате каких – либо математических операций над измеренной величиной х. (Например, f = х²).

Абсолютная погрешность будет определяться разностью между значениями f когда и когда :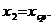

При малых можно считать, что

при

- первая производная функции f по х. Т.е. абсолютная погрешность функции одной переменной равна произведению производной этой функции на приращение аргумента.

В случае, если функция представляет собой зависимость от нескольких переменных

то абсолютная погрешность такой функции будет равна сумме произведений частных производных функции по каждой переменной на приращение этой переменной, т.е.

(6)

Относительная погрешность f будет, как обычно:

(7)

Из курса математики известно, что

(8)

Поэтому, для расчета относительной погрешности косвенных измерений следует сначала функцию прологарифмировать, а затем найти дифференциал:

ЛАБОРАТОРНАЯ РАБОТА №2