Адиабатический процесс. Политропный процесс.
Адиабатическим называется процесс, при котором отсутсвует теплообмен (dQ=0) между системой и окружающей средой. К адиабатическим процессам можно отнести все быстропротекающие процессы.
Из первого начала термодинамики для адиабатического процесса следует, что 
Поизведя некоторые преобразования из этого выражения получим уравнение адиабатического процесса, также называемое уравнением Пуассона.
 где g=Cp/CV - показатель адиабаты
где g=Cp/CV - показатель адиабаты
Работа при адиабатическом процессе равна

Изохорный, изобарный, изотермический и адиабатический процессы имеют общую особенность - они происходят при постоянной теплоемкости. Процесс, в котором теплоемкость остается постоянной, называется политропным. Уравнение политропы, исходя из первого начала термодинамики, выглядит так:  где
где 




Задача: 






Изменение энтропии зависит от начального и конечного состояния, только так может быть рассчитан для любого процесса вообще. Мы будем оценивать изменение энтропии по паре линий, показанных выше. Тогда...
Билет №18.
Случайные события. Вероятность. Функция распределения.
Вероятность события называется предел, к которому стремится отношение числа опытов, приводящих к его осуществлению, к общему числу опытов при беспредельном увеличении последнего. Если из N опытов N` приводят к реализации интересующего нас событитя, то вероятность W этого события выражается формулой: 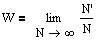 В термодинамике необходимо знать вероятность встречи молекул в определенном интервале скоростей. Эту вероятность называют распределением по скоростям и записывают в виде
В термодинамике необходимо знать вероятность встречи молекул в определенном интервале скоростей. Эту вероятность называют распределением по скоростям и записывают в виде 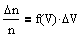 Функция f(V) называется функцией распределения.
Функция f(V) называется функцией распределения.
Система – конечная область пространства, с находящейся в ней объектов исследования. Определенная система предполагает наличие границ (воображ. или матер, подвижных или нет) Мы изучаем состояние системы из идеального газа:
а) Макроскопическое. Пусть в некотором изолированном объеме есть газ. Если температура в некоторый момент времени разная, то через некоторое время она выровнится и газ перейдет в стационарное состояние, где P, V, T – параметры. Состояние, где характеризующееся параметрами P, V, T, называется макроскопическим.
б) Микроскопическое. Состояние газа, характеризуемое положением и скоростями всех его частиц называется микроскопическим. Если в системе имеется n частиц, то в n-величин характеризуется его микроскопическое состояние. n=2,7*1019 см-3. Связь между а) и б): Каждому макроскопическому состоянию соответствует громадное количество микроскопических состояний.
Задача:(наша задача б)
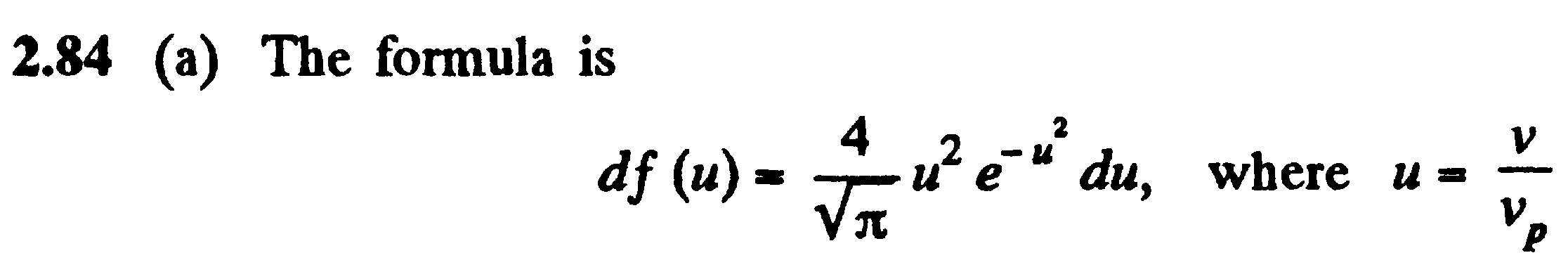 (prob – исследовать)
(prob – исследовать)
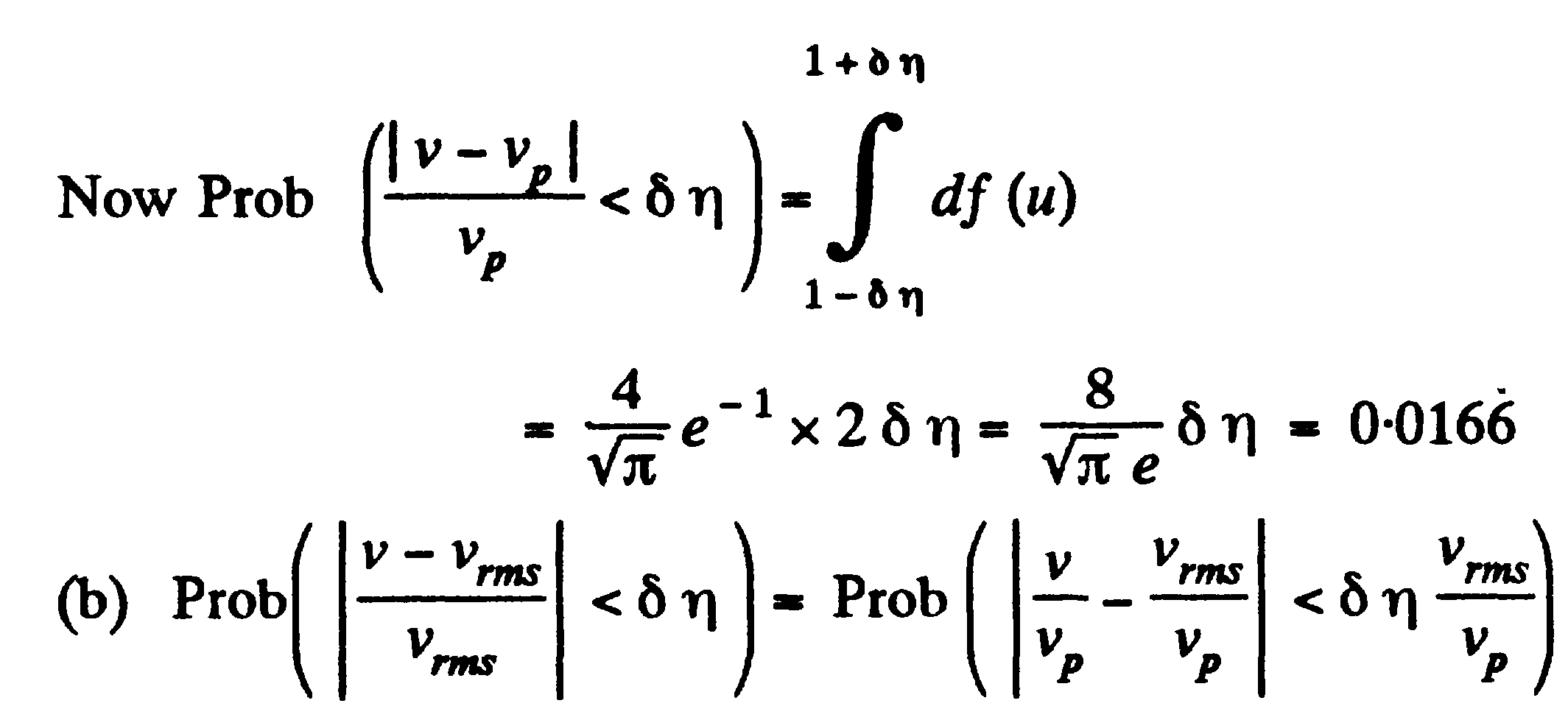 à
à 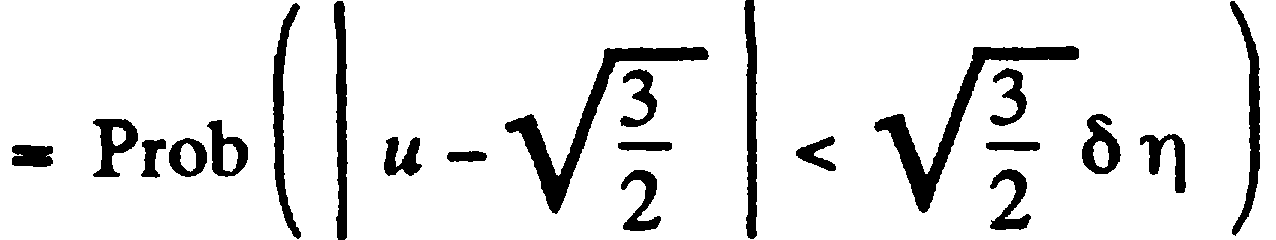 à
à 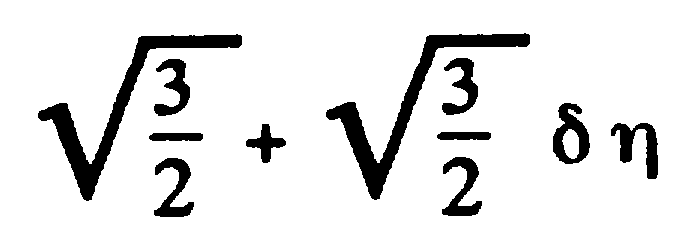
è 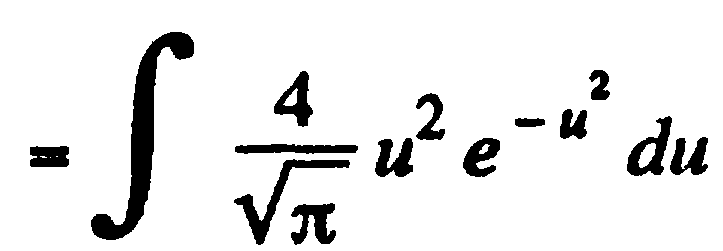 à
à 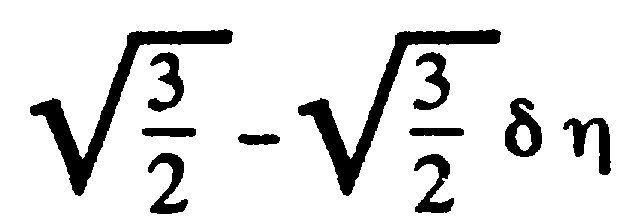 à
à 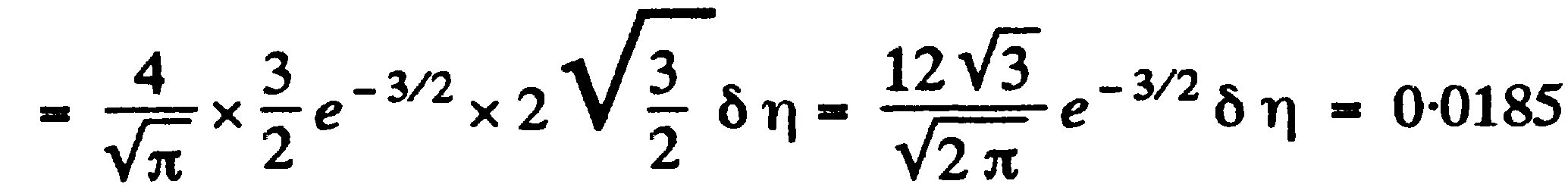
Билет №19.
Барометрическая формула.
Разность давлений p и p+dp равна весу газа, заключенного в объеме цилиндра высотой dh с основанием площадью 1 м2: 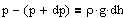
где r- плотность газа на высоте h (dh насолько мало, что при изменении высоты в этом пределе плотность газа можно считать постоянной). Следовательно, 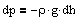
Воспользовавшись уравнением состояния идеального газа pV=(m/M)RT (m - масса газа, M - молярная масса газа), находим, что 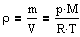
Подставим плотность и получим 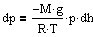 à
à 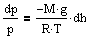
С изменением высоты от h1 до h2 давление изменяется от p1 до p2 т.е.
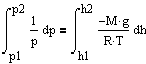 à
à 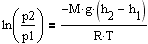 à
à 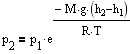 - барометрическая формула.
- барометрическая формула.
Так как высоты обозначаются относительно уровня моря, где давление считается нормальным, то выражение может быть записано в виде 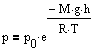
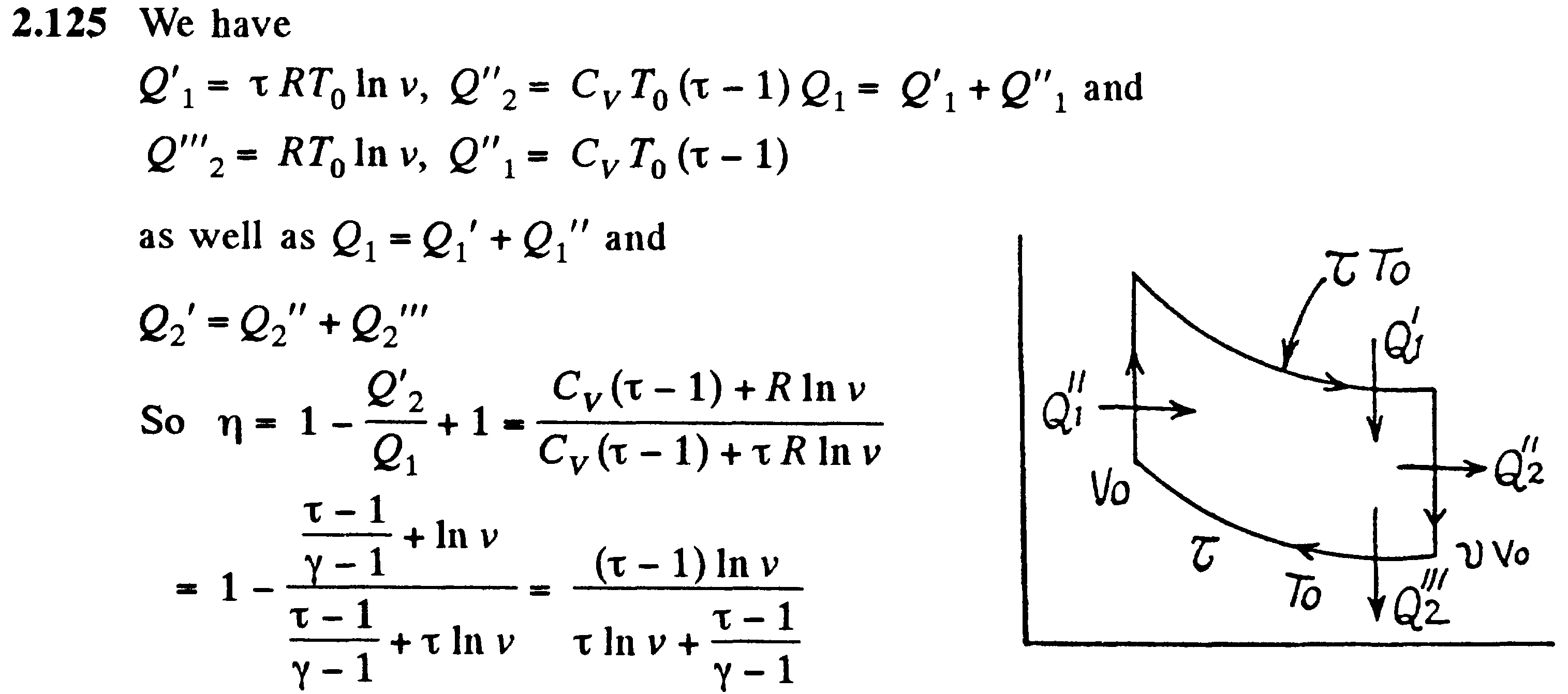
Билет №20.
