Энтропия. Неравенство Клаузиуса.
Билет №1.
Фазовые переходы первого и второго рода. Уравнение Клайперона-Клаузиуса.
1. Фазовыий переход(переход вещества из одной фазы в другую) всегда связан с качественными изменениями свойств вещества. Различают фазовые переходы двух родов.
Фазовый переход первого рода(например, плавление. кристаллизация) сопровождается поглащение или выделением теплоты, называемой теплотой фазового перехода.Фазовые переходы первого рода характеризуются постоянством температуры. изменениями энтропии и объема.
Фазовые переходы, не связаные с поглощением или выделением теплоты и изменением объема, называются фазовыми перехода второго рода
Эти переходы характеризуются постоянством объема и энтропии, но скачкообразным изменением теплоемкости. Фазовые переходы второго рода связаны с изменением симметрии: выше точки перехода система, как правило, обладает более высокой симметрией, чем ниже точек перехода.
В подобных переходах - из более упорядоченного кристаллического состояния в менее упорядоченное жидкое состояние степень беспорядка увеличивается, то есть согласно второму началу термодинамики, этот процесс связан с возрастанием энтропии системы. Если переход происходит в обратным направлении (кристаллизация), то система теплоту выделяет.
2.Для наглядного изображения фазовых превращений используется диаграмма состояния, на которой в координатах p, T задается зависимость между температурой фазового перехода и давлением в виде кривых испарения, плавления и сублимации, разделяющих поле диаграммы на три области. соответствующие условиям существования твердой, жидкой и газообразной фаз. Кривые на диаграмме называются кривыми фазовыми равновесия. Термодинамика дает метод расчета кривой равновесия двух фаз одного и того же вещества. Согласно уравнению Клапейрона-Клаузиуса. производная от давления по температуре равна
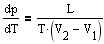
где L-теплота фазового перехода, (V2-V1) - изменение объема вещества при переходе его из первой фазы во вторую, T - температура перехода (процесс изотермический). Уравнение Клайперона-Клаузиуса позволяет определять наклоны кривых равновесия.
Задача: Если проявленная сила - F, тогда закон изменения концентрации с высотой читается:…
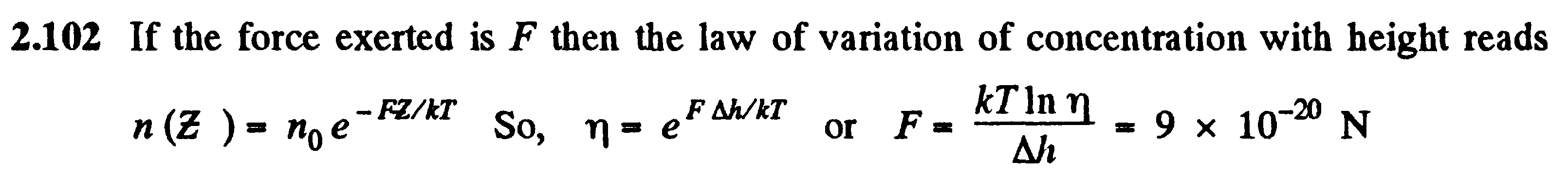
Билет №2.
Распределение Максвелла.
Распределение Максвелла задает распределение молекул газа по скоростям при их хаотическом тепловом движении. Случайные столкновения молекул при их движении в газе приводят к случайным же изменениям их скоростей как по величине, так и по направлению. Скорость молекул удобно изобразить точкой в 3-х мерном пространстве скоростей. Совокупность скоростей всех молекул газа заполнит пространство скоростей с некоторой плотностью, пропорциональной плотности вероятности нахождения того или иного значения скорости. Вдоль любого направления в пространстве скоростей случайные отклонения в ту или иную сторону равновероятны, поэтому в качестве функции распределения для этого направления можно взять распределение Гаусса. Так как все направления равновероятны, то меры точности вдоль каждого из них должны быть одинаковыми, поэтому для функции распределения компонент скоростей имеем
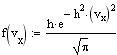
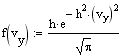
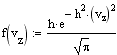
Ввиду независимости компонент скорости, пользуясь теоремой об умножении вероятностей, получаем
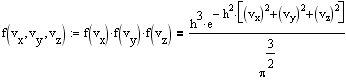
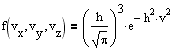
Среднее значения квадратов компонент скоростей одинаковы и равны <vx2> =<vy2> =<vz2> = 1/2h2. Средняя кинетическая энергия молекулы массой m равна 3kT/2, следовательно
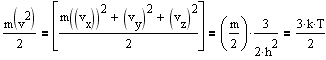
Откуда
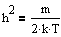
Получим распределение Максвелла по компонентам скоростей:
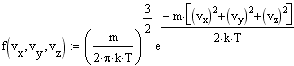
Для нахождения распределения молекул по модулю скорости перейдем в сферическую систему координат и, интегрируя по углам. найдем относилельное число молекул, обладающих скоростью от v до v+dv:
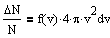 , откуда получим функцию распределения:
, откуда получим функцию распределения:
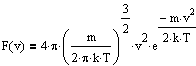
F(v) называется распределением Максвелла по модулю скорости v.
Задача:Рассматриваемый процесс может быть записан как 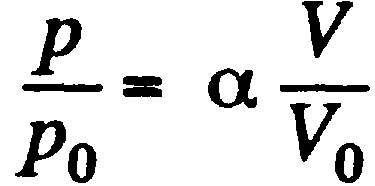 где α – постоянная, p, V - некоторые значения. Для этого процесса характерно:
где α – постоянная, p, V - некоторые значения. Для этого процесса характерно: 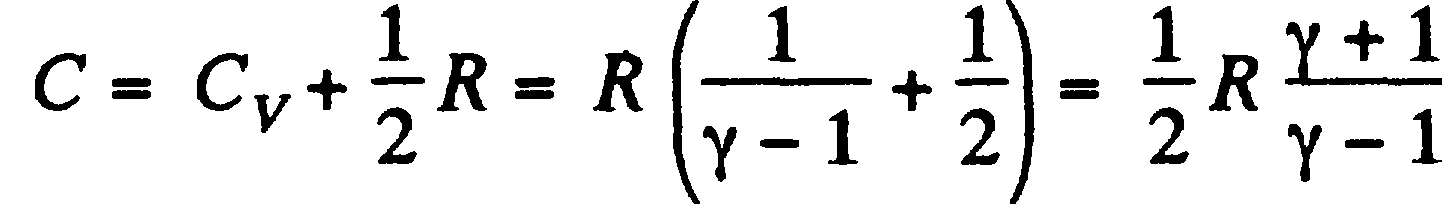 По объему линейно увеличивается α как и давление. Температура должна тогда увеличиться α в квадрате по времена. Таким образом:
По объему линейно увеличивается α как и давление. Температура должна тогда увеличиться α в квадрате по времена. Таким образом: 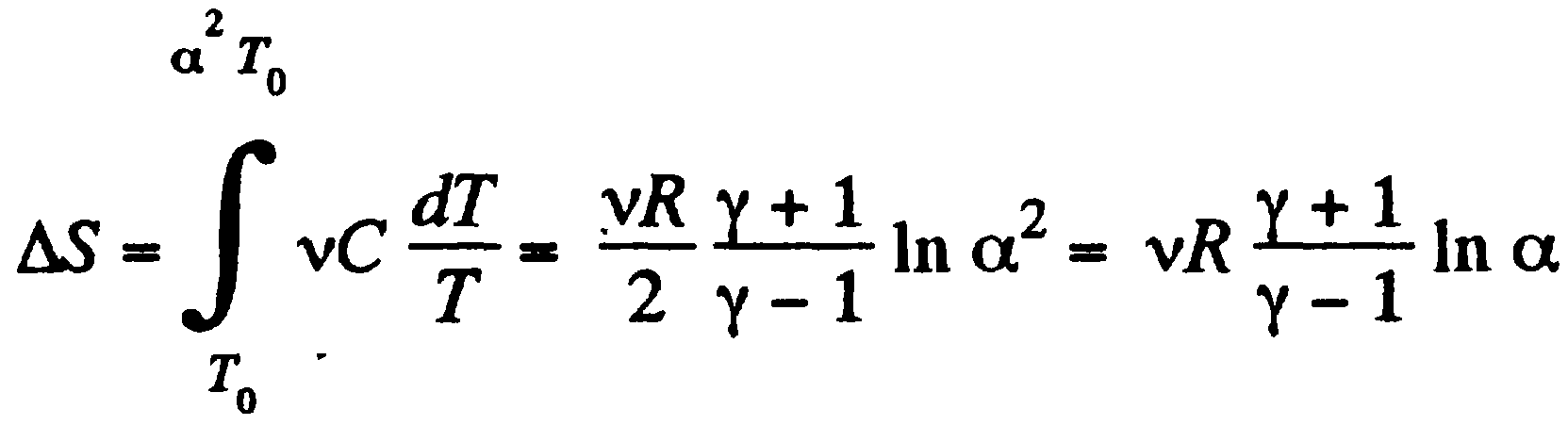
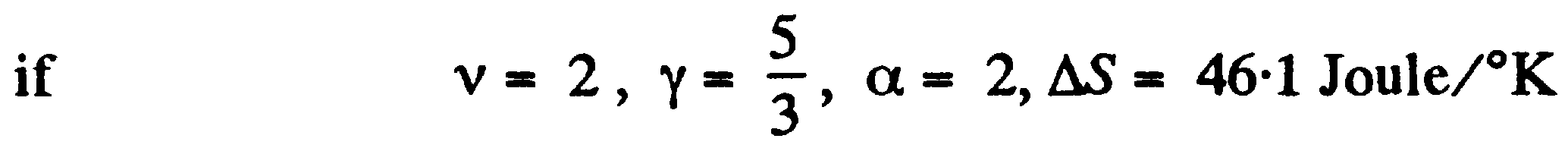
Билет №3.
Отступление от законов идеальных газов. Уравнение Ван-дер-Ваальса.
Для реальных газов необходимо учитывать размеры молекул и их взаимодействие друг с другом, поэтому модель идеального газа и уравнение Клайперона-Менделеева
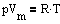
(для моля газа), описывающее идеальный газ, для реальных газов непригодны.
Учитывая собственный объем молекул и силы межмолекулярного взаимодействия, Ван-дер-Ваальс вывел уравнение состояния реального газа. Он ввел в уравнение Клайперона-Менделеева введены две поправки.
1.Учет собственного объема молекул. Наличие сил отталкивания, которые противодействуют проникновению в занятый молекулой объем других молекул, сводится к тому, что фактический свободный объем, в котором могут двигаться молекулы реального газа, будет не Vm, a Vm - b, где b - объем, занимаемый самими молекулами. Объем b равен учетверенному собственному объему молекул.
2. Учет притяжения молекул.Действие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого внутренним давлением. По вычислениям Ван-дер-Ваальса, внутреннее давление обратно пропорционально квадрату молярного объема, т. е.
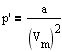
где a - постоянная Ван-дер-Ваальса, хараактерезующая силы межмолекулярного притяжения, Vm - молярный объем.
Вводя эти поправки. получим уравнение Ван-дер-Ваальса для моля газа (уравнение состояния реальных газов):
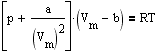
Для произвольного количества вещества n газа с учетом того, что V=nVm, уравнение Ван-дер-Ваальса примет вид
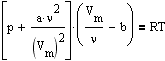
или
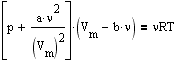
где поправки a и b - постоянные для каждого газа велечины, определяемые опытгным путем.
Задача: 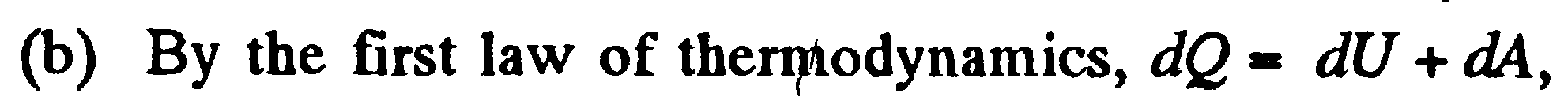 или
или 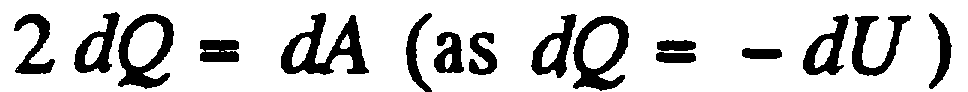 ,
, 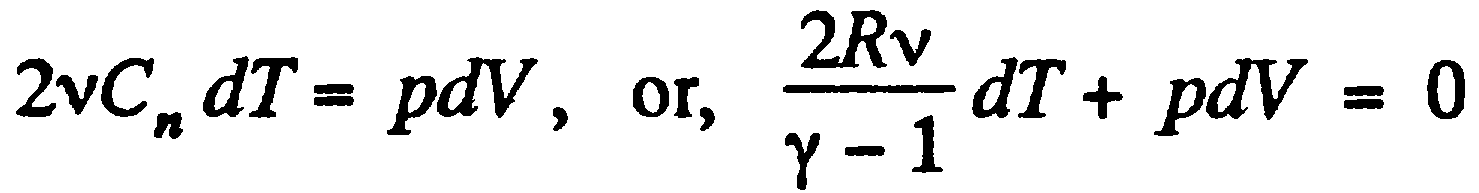
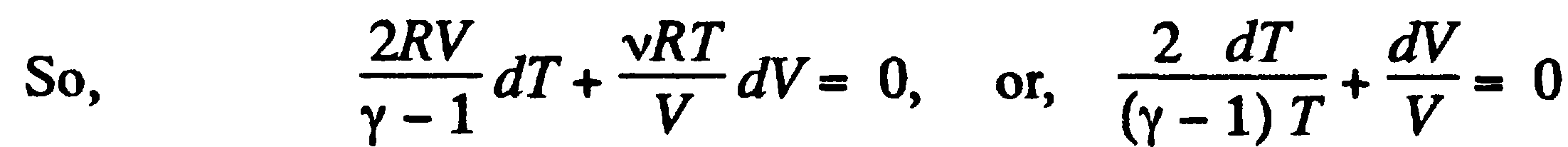 , или
, или 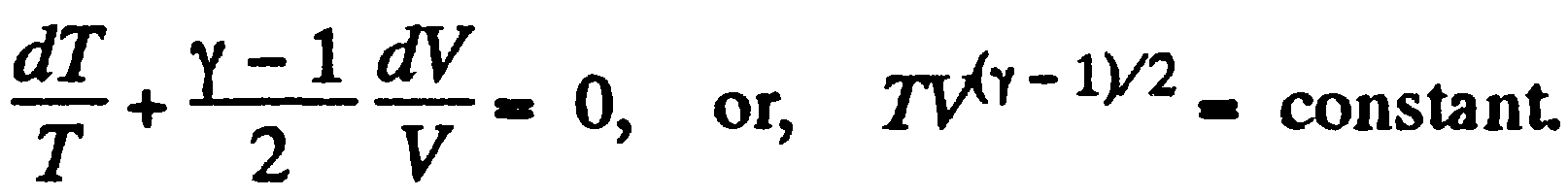
Билет №4.
Уравнение Ван-дер-Ваальса после несложных преобразований можно привести к виду:
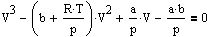
Это уравнение третьей степени относительно объема V и оно поэтому имеет три корня. Это значит , что при данных значениях температуры и давления могут быть три значения молярного объема или, что то же самое, три значения плотности газа.
В отличие от изотермы идеального газа, представляющей собой гиперболу, изотерма, соответствующая уравнению, которую назовем изотермой Ван-дер-Ваальса. Эта кривая, являющаяся графическим изображением уравнения третьей степени, имеет максимум и минимум, так что данному значению давления соответствуют три значения молярного объема. Естественно считать, что минимальному из этих значений объема соответствует жидкое состояние, а максимальному - газообразное.
Задача: (где Cn – молярная теплоёмкость газа в этом процессе. Этому даёт, что)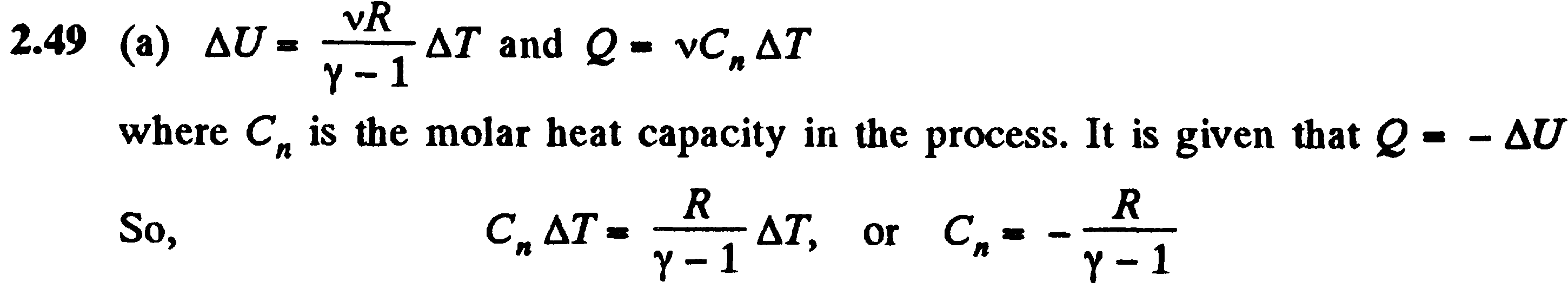
Билет №5,6.
Билет №7.
Три начала термодинамики.
Термодинамика – раздел физики, в котором изучается условие превращения одного вида энергии в другое и количественное отношение при этих превращениях.
Рассмотрим термодинамическую систему, для которой механическая энергия не изменяется, а изменяется лишь ее внутренняя энергия. Внутренняя энергия системы может изменяться в результате различных процессов, например совершения над системой работы или сообщения ей теплоты. 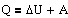
Это уравнение выражает первое начало термодинамики: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил. Первое начало термодинамики в дифференциальной форме будет иметь вид
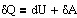
Если система периодически возвращается в первоначальное состояние, то изменение ее внутренней энергии DU=0. Тогда, согласно первому началу термодинамики, A=Q, т.е. вечный двигатель первого рода - периодически действующий двигатель, который совершал бы работу большую. чем сообщенная ему из вне энергия, - невозможен.
Используя понятие энтропии и неравенство Клаузиуса (DS>=0), второе начало термодинамики можно сформулироватькак закон возрастания энтропиизамкнутой системы при необратимых процессах: любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает.
Можно дать более краткую формулировку второго начала тд: в процессах, происходящих в замкнутой системе, энтропия не убывает.
Первые два начала тд дают недостаточно сведений о поведении термодинамических систем при нуле Кельвина. Она дополняются третьим началом тд, или теоремой Нернста-Планка: энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина.
Билет №8.
Цикл Карно. Его к.п.д.
Основываясь на втором начале термодинамики, Карно вывел теорему: из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей (T1) и холодильников (T2), наибольшим к.п.д. одладают обратимые машины; при этом к.п.д. обратимых машин, работающих при одинаковых температурах нашревателей (T1) и холодильников (T2), равны друг другу и не зависят от природы рабочего тела, а определяются только температурами нагревателя и холодильника.
Цикл Карно изображен на рисунке (НАРИСОВАТЬ!!!!), где изотермические расширение и сжатие заданы соответсвенно кривыми 1-2 и 3-4, а адиабатические расширения и сжатия - кривыми 2-3 и 4-1.
Термический к.п.д. цикла Карно
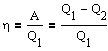
Применив уравнение для адиабат 2-3 и 4-1, получим
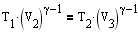
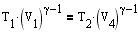
откуда
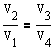
Подставляя эти выражения в формулу к.п.д., получаем
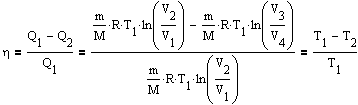
т.е. для цикла Карно к.п.д. действительно определяется только температурами нагревателя и холодильника. Для его повышения необходимо увеличить разность температур нагревателя и холодильника. К.п.д. всякого реальеного теплового двигателя из-за трения и неизбежных тепловых потерь гораздо меньше вычисленного для цикла Карно.
Задача: 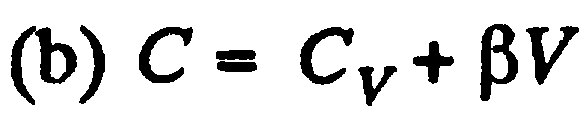
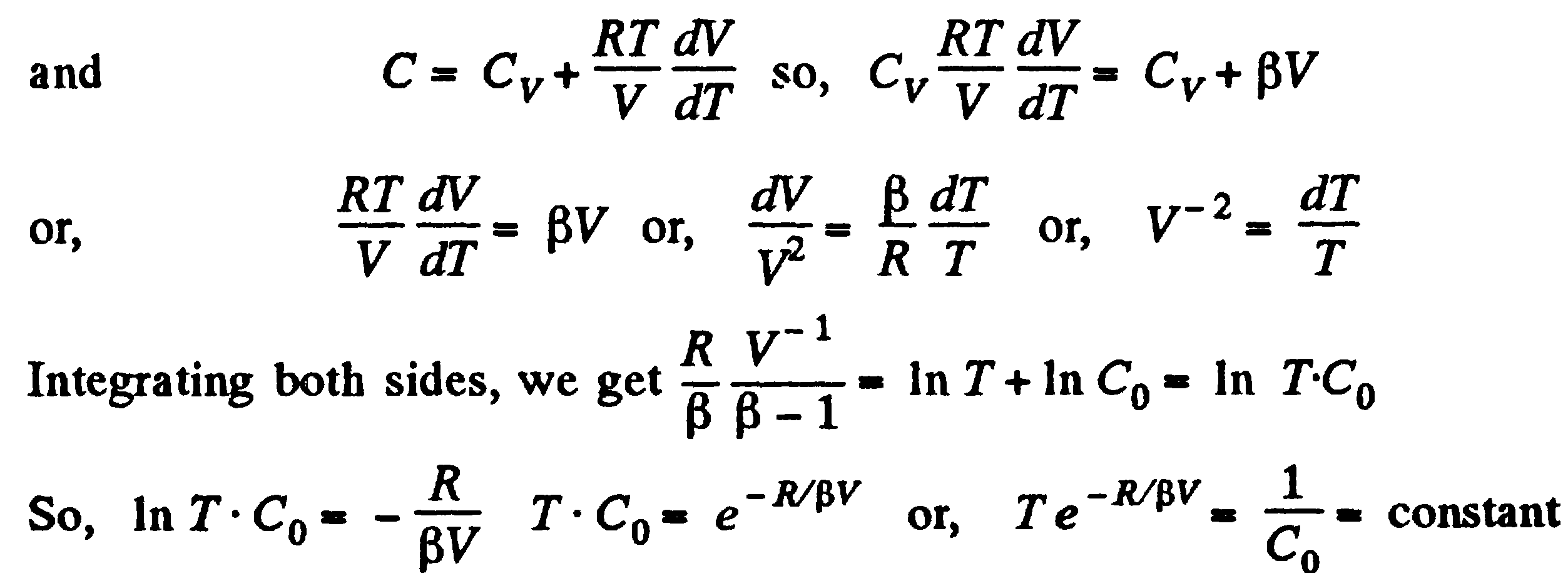 объединяя обе стороны, мы получаем
объединяя обе стороны, мы получаем
Билет №9.
Обратимые и необратимые процессы. Тепловые двигатели и холодильные машины.
Термодинмический процесс называется обратимым, если он может происходить как в прямом, так и обратном направлении, причем если такой процесс происходит сначала в прямом, затем в обратном направлении и система возвращается в исходное состояние, то в окружающей среде не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым.
Любой равновесный процесс является обратимым. Обратимость равновесного процесса, происходящего в системе, следует из того, что ее любое промежуточное состояние есть состояние термодинамического равновесия; для него "безразлично", идет процесс в прямом или обратном направлении. Реальные процессы сопровождаются диссипацией энергии (из-за трения, теплопроводности и т.д.). Обратимые процессы - это идеализация реальных процессов.
Тепловой двигатель - периодически действующий двигатель, совершающий работу за счет охлаждения одного источника теплоты. Принцип действия: от термостата с более высокой температурой T1, называемого нагревателем, за цикл отнимается количество Q1, термостату с более низкой температурой T2, называемому холодильникком, за цикл передается количество теплоты Q2, при этом совершается работа A=Q1-Q2
Процесс, обратный происходящему в тепловом двигателе, используется в холодильной машине. Системой за цикл от термостата с более низкой температурой T2 отнимается количество теплоты Q2 и отдается термостату с более высокой температурой T1 количество теплоты Q1. Для кругового процесса Q=A, но, по условию, Q=Q2-Q1<0, поэтому A<0. Следовательно, без совершения работы нельзя отбирать теплоту от менее нагретого тела и отдавать ее более нагретому.
 Задача:
Задача: 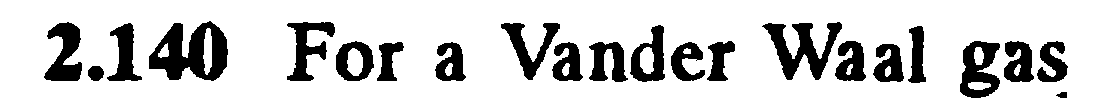
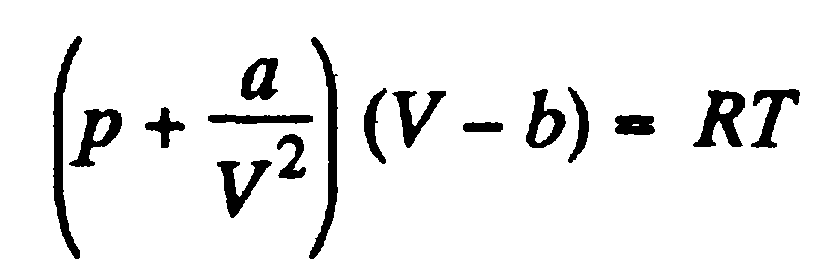
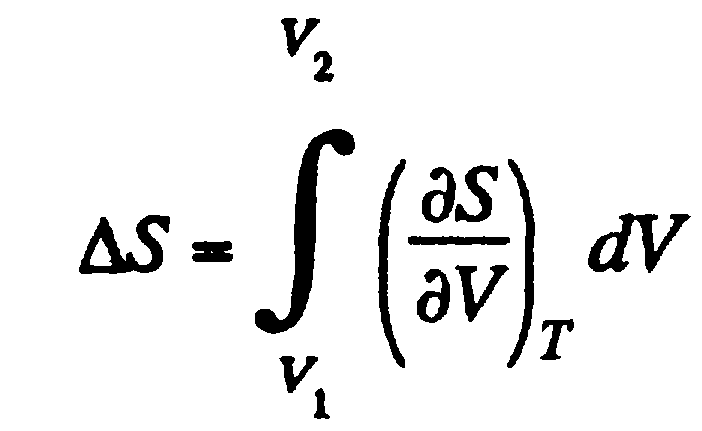 ,
, 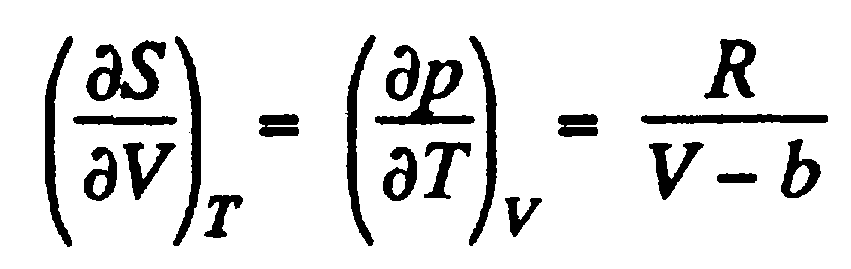 ,
, 
Или другая задача:
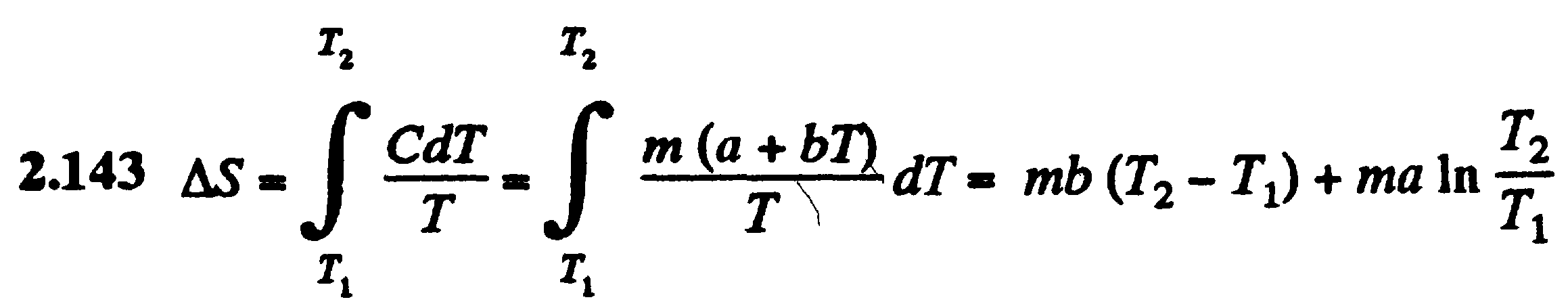
Билет №10.
Явление переноса. Уравнение переноса.
В тд неравновесных системах возникают особые необратимые процессы, называемые явлениями переноса, в результате оторых происходит пространственный перенос энергии(теплопроводность), массы(дифузия), импульса(внуртеннее трение)
1. Теплопроводность. Выравнивание средних кинетических энергий молекул, иными словами, выравнивание температур.
2.Диффузия. Явление дуффузии заключается в том, что происходит самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел; диффузия сводится к обмену масс частиц этих тел, возникает и продолжается пока существует градиент плотности.
3. Внутреннее трение (вязкость). Механизм возникновения внутреннего трения между параллельными слоями газа (жидкости), движущимся с различными скоростями, заключается в том, что из-за хаотичного теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя. движущегося быстрее, уменьшается, движущегося медленнее - увеличивается, что приводит к торможению слоя. движущегося быстрее, и ускорению слоя. движущегося медленнее.
Динамическая вязкость η численно равна плотности потока импульса при градиенте скорости, равном единице; она вычисляется по формуле
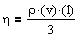 ,
, 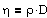 ,
, 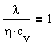
Задача:
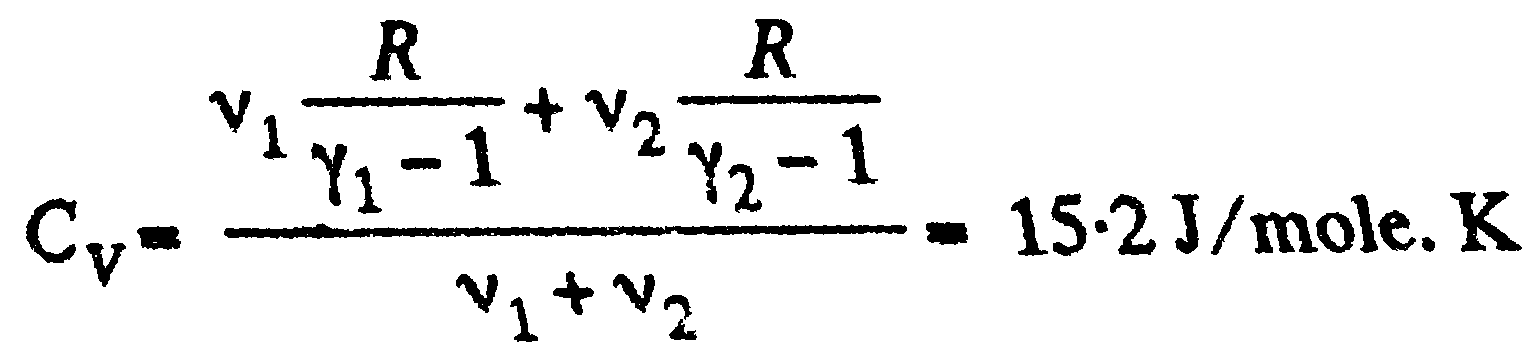
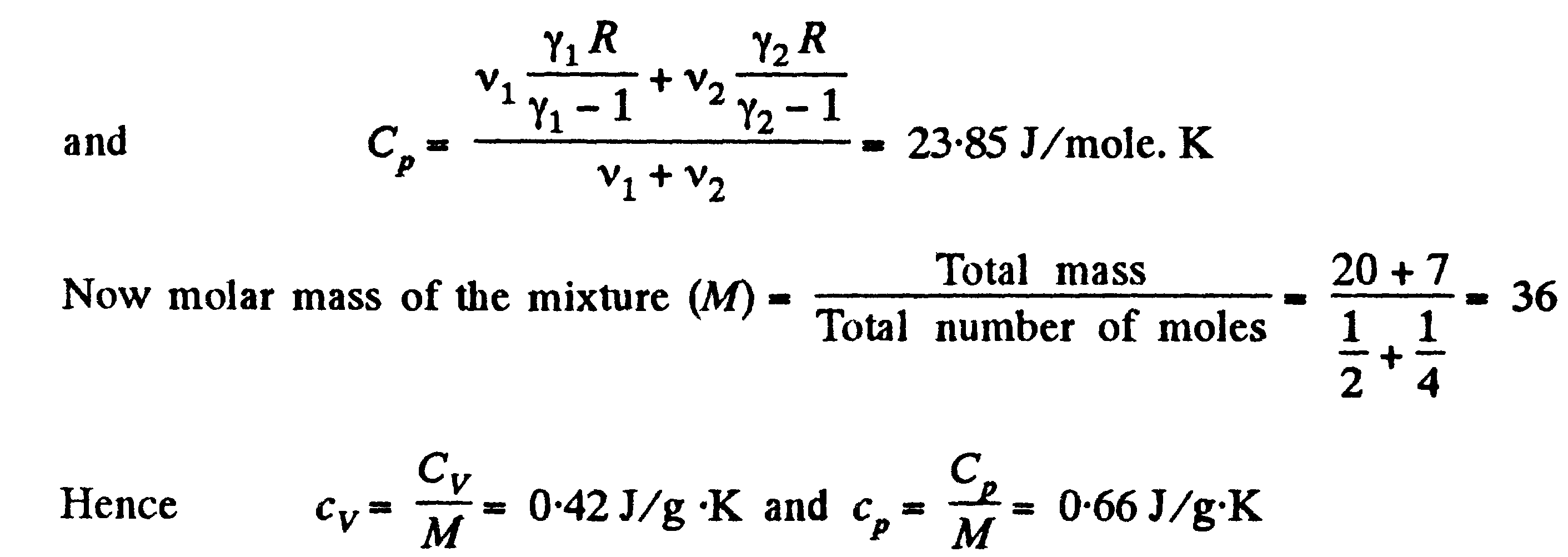
Теперь молярная масса смеси (М) = (полная масса)/(общее кол-во молей) = … следовательно…
Билет №11.
Распределение Максвелла.
Распределение Максвелла задает распределение молекул газа по скоростям при их хаотическом темпловом движении. Случайные столкновения молекул при их движении в газе приводят к случайным же изменениям их скоростей как по величине, так и по направлению. Скорость молекул удобно изобразить точкой в 3-х мерном пространстве скоростей. Совокупность скоростей всех молекул газа заполнит пространсто скоростей с некоторой плотностью, пропорциональной плотносмти вероятности нахождения того или иного значения скорости. Вдоль любого направления в пространстве скоростей случайные отклонения в ту или иную сторону равновероятны, поэтому в качестве функции распределения для этого направления можно взять распределение Гаусса. Так как все направления равновероятны, то меры точности вдоль каждого из них должны быть одинаковыми, поэтому для функции распределения компонент скоростей имеем
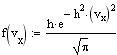
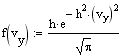
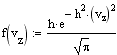
Ввиду независимости компонент скорости, пользуясь теоремой об умножении вероятностей, получаем
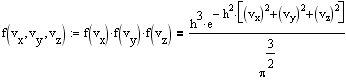
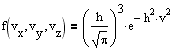
Среднее значения квадратов компонент скоростей одинаковы и равны <vx2> =<vy2> =<vz2> = 1/2h2. Средняя кинетическая энергия молекулы массой m равна 3kT/2, следовательно
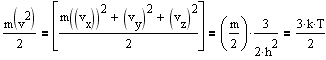
Откуда 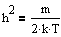
Получим распределение Максвелла по компонентам скоростей:
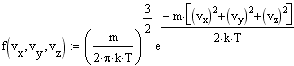
Для нахождения распределения молекул по модулю скорости перейдем в сферическую систему координат и, интегрируя по углам. найдем относилельное число молекул, обладающих скоростью от v до v+dv:
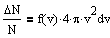 , откуда получим функцию распределения:
, откуда получим функцию распределения:
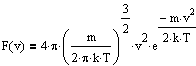 F(v) называется распределением Максвелла по модулю скорости v.
F(v) называется распределением Максвелла по модулю скорости v.
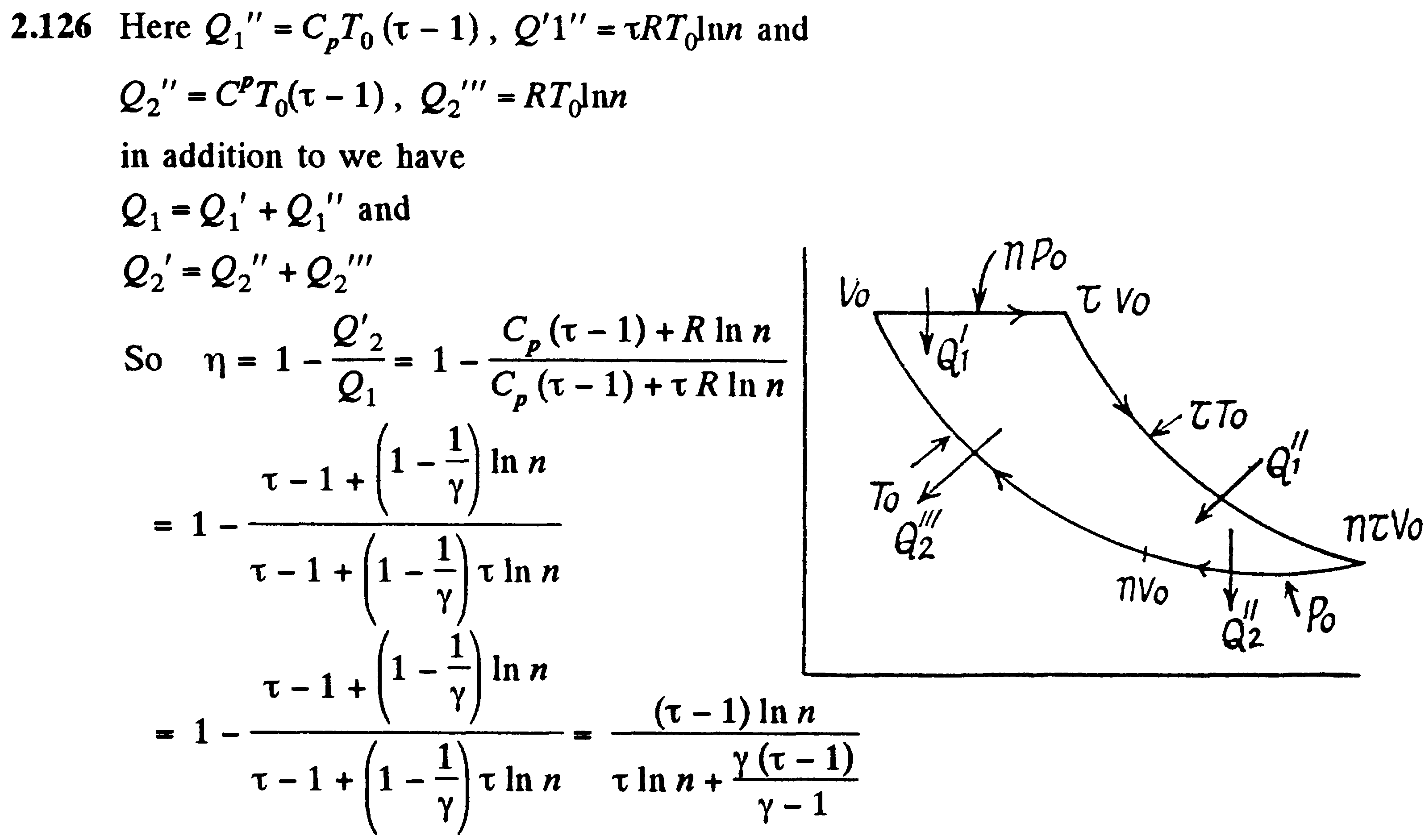
Билет №12.
Распределение Больцмана.
Выведем закон изменения давления с высотой, предпологая, что поле тяготения однородно, температура постоянна и масса всех молекул одинакова. Если атмосферное давление на высоте h равно p, то на высоте h+dh оно равно p+dp (при dh>0 dp<0, так как давление с высотой убывает). Разность давлений p и p+dp равна весу газа, заключенного в объеме цилиндра высотой dh с основанием площадью 1 м2: 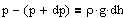
где r- плотность газа на высоте h (dh насолько мало, что при изменении высоты в этом пределе плотность газа можно считать постоянной). Следовательно, 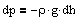
Воспользовавшись уравнением состояния идеального газа pV=(m/M)RT (m - масса газа, M - молярная масса газа), находим, что 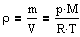
Подставим плотность и получим
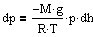 à
à 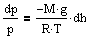
С изменением высоты от h1 до h2 давление изменяется от p1 до p2 т.е.
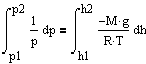 à
à 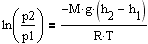 à
à 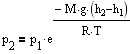
Выражение называется барометрической формулой. Она позволяет найти атмосферное давление в зависимости от высоты или, измерив давление, найти высоту. Так как высоты обозначаются относительно уровня моря, где давление считается нормальным, то выражение может быть записано в виде 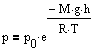
Барометрическую формулу можно преобразовать, если воспользоваться выжением p=nkT:
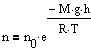
где n - концентрация молекул на высоте h, n0 - то же, на высоте h=0. Так как M=m0NA ((NA - постоянная Авогадро, m0 - масса одной молекулы), а R=kNA, то
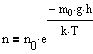 где m0gh=P - потенциальная энергия молекулы в поле тяготения, т.е.
где m0gh=P - потенциальная энергия молекулы в поле тяготения, т.е. 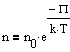
Полученное выражение называется распределением Больцмана для внешнего потенциального поля. Из него следует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.Если частицы имеют одинаковую массу и находятся в состоянии хаотического теплового движения, то распределения Больцмана справедливо в любом внешнем потенциальном поле, а не только в поле сил тяжести.
Закон Больцмана о распределении энергии по степеням свободы молекул: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднекинетическая энергия, равная kT/2, а на каждую колебательную степень свободы - в среднем энергия, равная kT.
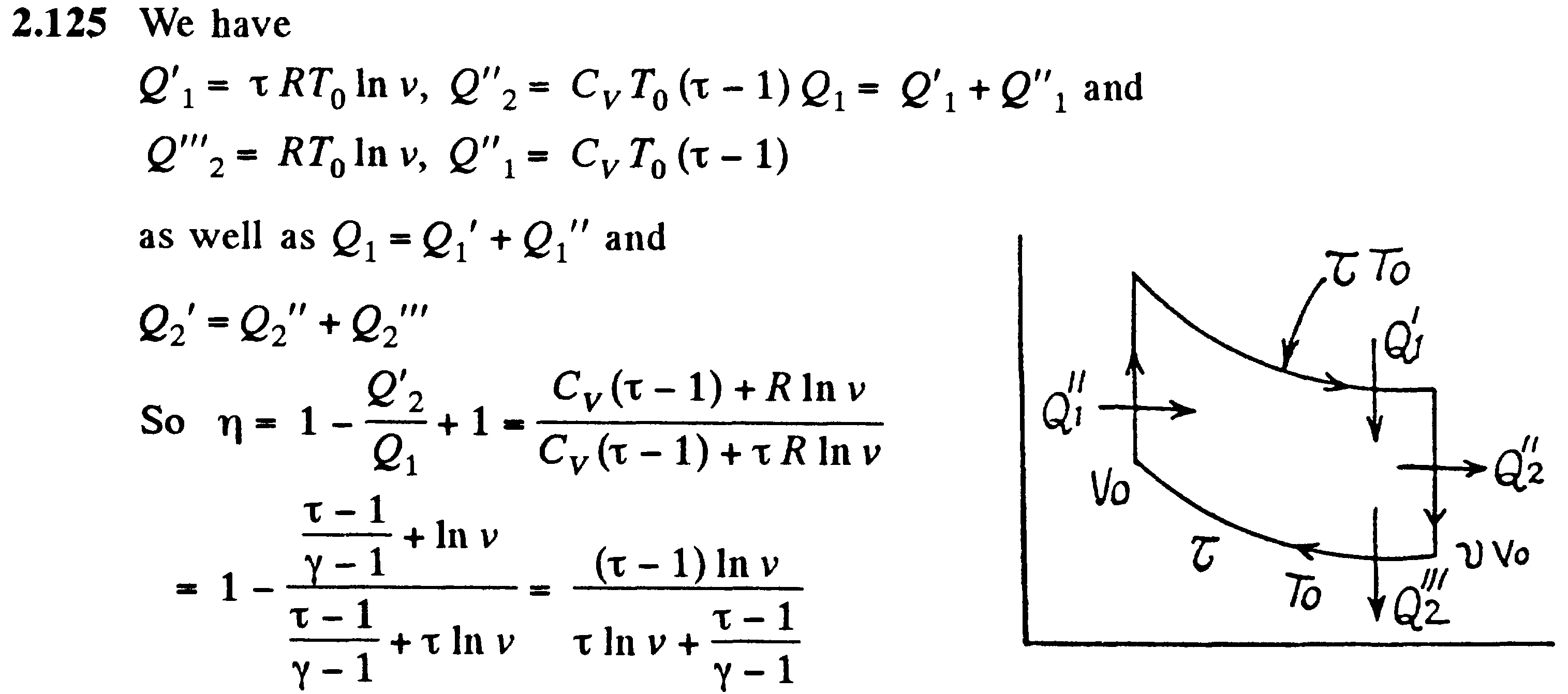
Билет №13.
Распределение Максвелла.
Распределение Максвелла задает распределение молекул газа по скоростям при их хаотическом темпловом движении. Случайные столкновения молекул при их движении в газе приводят к случайным же изменениям их скоростей как по величине, так и по направлению. Скорость молекул удобно изобразить точкой в 3-х мерном пространстве скоростей. Совокупность скоростей всех молекул газа заполнит пространсто скоростей с некоторой плотностью, пропорциональной плотносмти вероятности нахождения того или иного значения скорости. Вдоль любого направления в пространстве скоростей случайные отклонения в ту или иную сторону равновероятны, поэтому в качестве функции распределения для этого направления можно взять распределение Гаусса. Так как все направления равновероятны, то меры точности вдоль каждого из них должны быть одинаковыми, поэтому для функции распределения компонент скоростей имеем
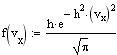
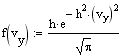
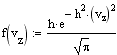
Ввиду независимости компонент скорости, пользуясь теоремой об умножении вероятностей, получаем
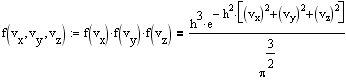
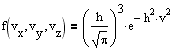
Среднее значения квадратов компонент скоростей одинаковы и равны <vx2> =<vy2> =<vz2> = 1/2h2. Средняя кинетическая энергия молекулы массой m равна 3kT/2, следовательно
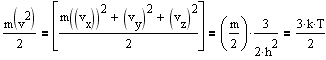
Откуда 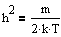
Получим распределение Максвелла по компонентам скоростей:
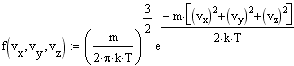
Для нахождения распределения молекул по модулю скорости перейдем в сферическую систему координат и, интегрируя по углам. найдем относилельное число молекул, обладающих скоростью от v до v+dv:
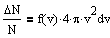 , откуда получим функцию распределения:
, откуда получим функцию распределения:
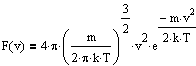 F(v) называется распределением Максвелла по модулю скорости v.
F(v) называется распределением Максвелла по модулю скорости v.
Задачу заменят!
Билет №14.
Капиллярные явления.
Если поместить узкую трубку (капиляр) одним концом в жидкость, налитую в широкий сосуд, то вследствие смачивания или не смачивания жидкостью стенок капилляра кривизна поверхности жидкости в капилляре становится значительной. Если жидкость смачивает материал трубки, то внутри ее поверхность жидкости - мениск - имеет вогнутую форму, если не смачивает - выпуклую.
Под вогнутой поверхностью жидкости появится отрицательное избыточное давление, определяемое по формуле Dp=-2s/R. Наличие этого давления приводит к тому, что жидкость в капилляре поднимается, так как под плоской поверхностью жидкости в широком сосуде избыточного давления нет. Если же жидкость не смачивает стенки капилляра, то положительное избыточное давление приведет к опусканию жидкости в капилляре. Явление изменения высоты уровня жидкости в капиллярах называется капиллярностью. Жидкость в капилляре поднимается или опускается на такую высоту h, при которой давление столба жидкости (гидростатическое давление) rgh уравновешивается избыточным давлением Dp, т.е. 2s/R=rgh, где r - плотность жидкости, g - ускорение свободного падения. Елси r - радиус капилляра, q - краевой угол, то h=(2scosq)/(rgh)
Капиллярные явления играют большую роль в природе и технике. Например, влагообмен в почве и в растениях осуществляется за счет поднятия воды по тончайшим капиллярам. На капиллярности основано действие фитилей, впитывание влаги бетоном и т.д.
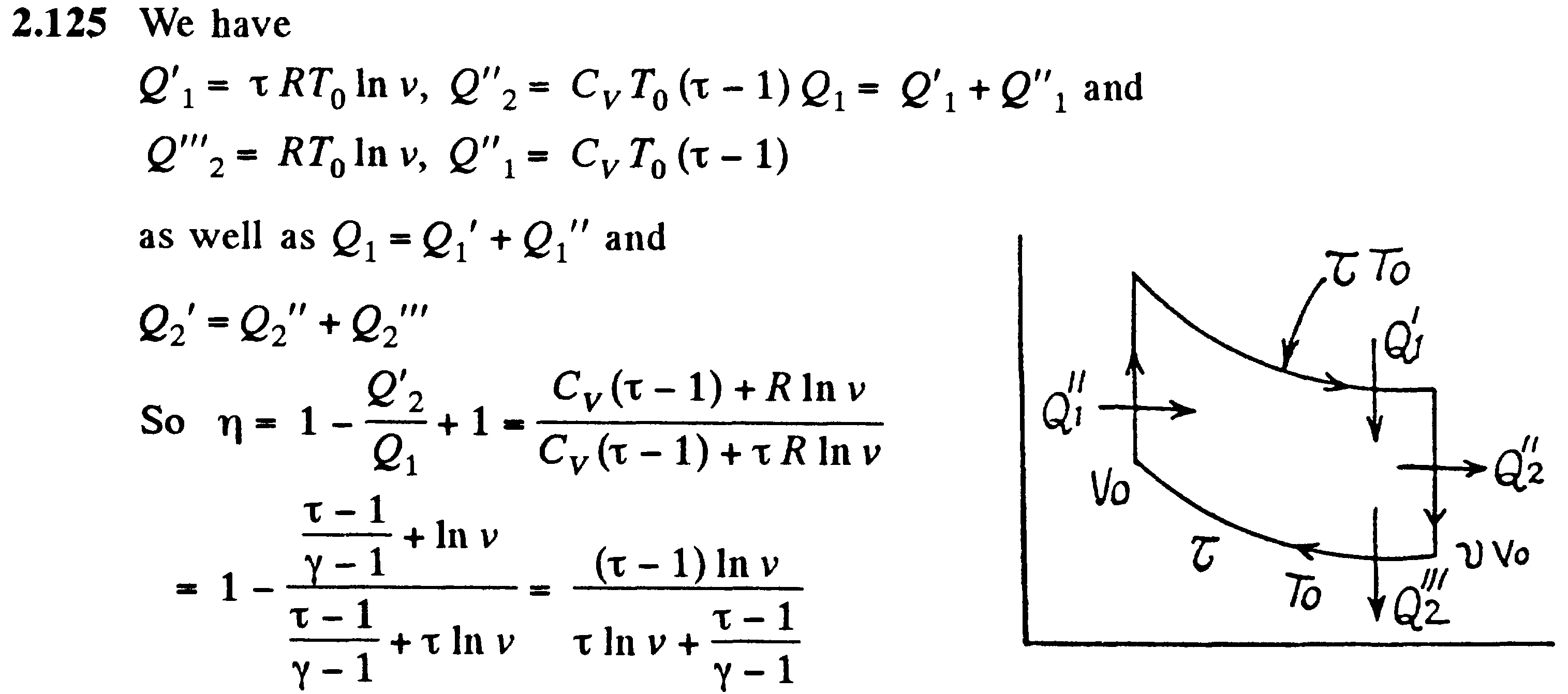
Билет №15.
Классическая молекулярно-кинетическая теория и ее ограниченность.
Учение о свойстве вещества.
1) Все вещества состоят из мельчайших частиц. (Атомов и молекул)
2) Частицы вещества находятся в непрерывном движении. (Движутся хаотически)
3) Между частицами есть силы взаимодействия (притягивания и отталкивания)
Потенциал Джонса U=a/r6--b/r12. Если Ek>Ep - газ. Ek<Ep - жидкость. Ek=Ep- твердое. P=1/3mV2 основное уравнение мкт.
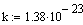
Дж/К
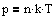 где n - концентрация
где n - концентрация
Уравнение состояния идеального газа.
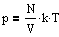 ,
, 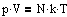 ,
, 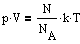 ,
, 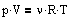
Задача:
Билет №16.
Теплоемкость при постоянном объеме и давлении.
Удельная теплоемкось вещества - величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К:
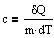
Единица удельной теплоемкости - джоуль на килограмм-кельвин (Дж/кг К)
Молярная теплоемкость - величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К:
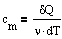 где n=m/M - количество вещества. Единица молярной теплоемкости - джоуль на моль-кельвин.
где n=m/M - количество вещества. Единица молярной теплоемкости - джоуль на моль-кельвин.
Удельная теплоемкость связана с молярным соотношением: cm=cM, где M - молярная масса вещесва.
Различают теплоемкости при постоянном объеме и постоянном давлении, если в процессе нагревания вещества его объем или давление поддерживается постоянным. Запишем первое начало термодинамики для 1 моль газа с учетом теплоемкости: 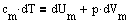
Если газ нагревается при постоянном объеме, то работа внешних сил равна нулю и сообщаемая газу извне теплота идет только на увеличение его внутренней энергии: 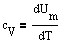
т. е. молярная теплоемкость газа при постоянном объеме СV равна изменению внутренней энергии 1 моль газа при повышении его температуры на 1 К. Согласно формуле
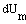 =(i/2)RdT, тогда
=(i/2)RdT, тогда 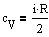
Если газ нагревается при постоянном давлении, то теплоемкость можно выразить в виде 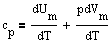
Изходя из выражения молярной теплоемкости при постоянном объеме и дифференциальной формы уравнения Клайперона - Менделеева получим 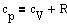
Это выражение называется уравнением Майера; он показывает, что 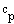 всегда больше
всегда больше 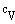 на величину молярно газовой постоянной.
на величину молярно газовой постоянной.
Задача:В политропическом процессе pVn =const, где n – индекс политропа. Для этого процесса…
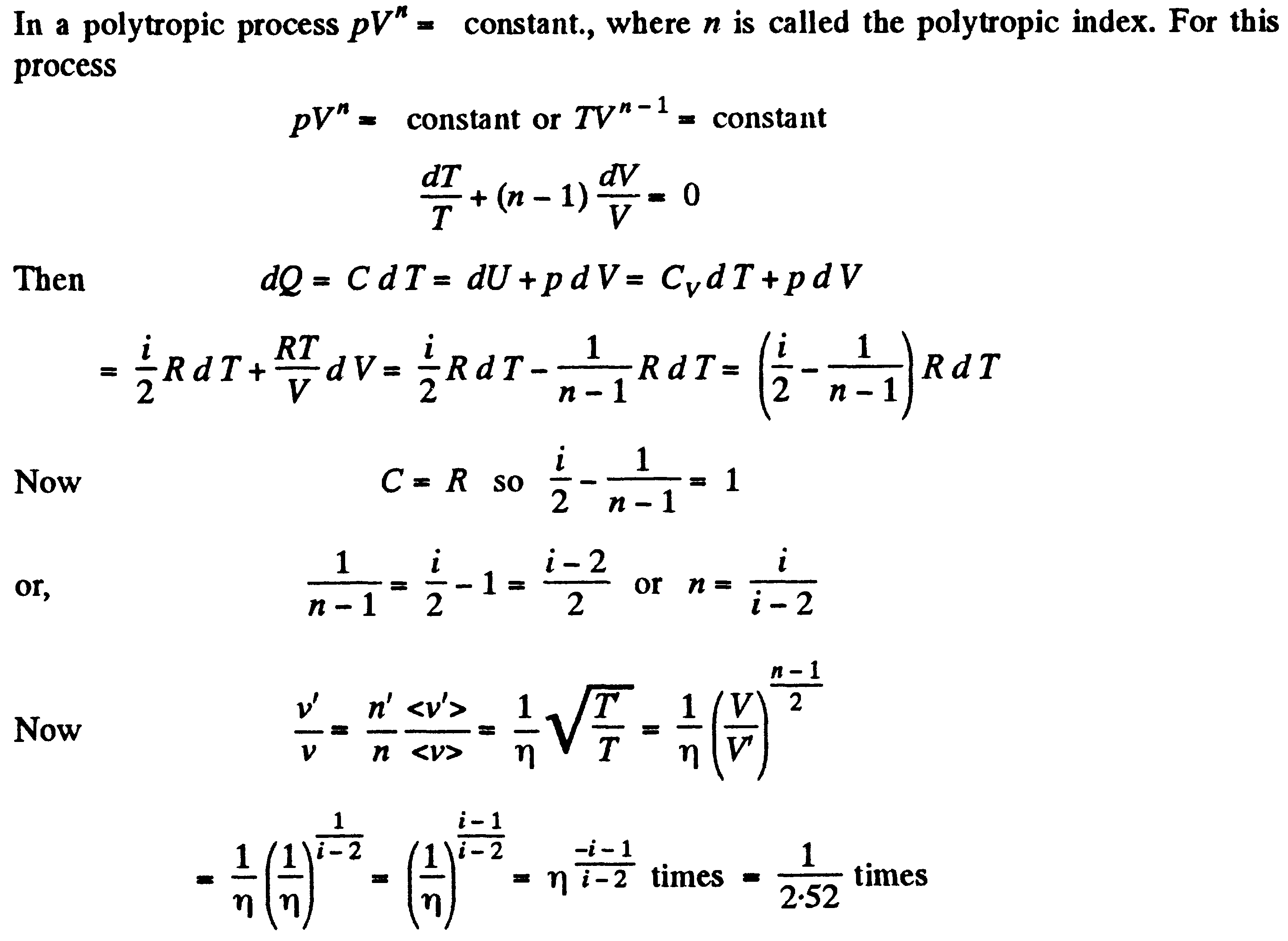
Билет №17.
Билет №18.
Случайные события. Вероятность. Функция распределения.
Вероятность события называется предел, к которому стремится отношение числа опытов, приводящих к его осуществлению, к общему числу опытов при беспредельном увеличении последнего. Если из N опытов N` приводят к реализации интересующего нас событитя, то вероятность W этого события выражается формулой: 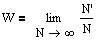 В термодинамике необходимо знать вероятность встречи молекул в определенном интервале скоростей. Эту вероятность называют распределением по скоростям и записывают в виде
В термодинамике необходимо знать вероятность встречи молекул в определенном интервале скоростей. Эту вероятность называют распределением по скоростям и записывают в виде 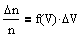 Функция f(V) называется функцией распределения.
Функция f(V) называется функцией распределения.
Система – конечная область пространства, с находящейся в ней объектов исследования. Определенная система предполагает наличие границ (воображ. или матер, подвижных или нет) Мы изучаем состояние системы из идеального газа:
а) Макроскопическое. Пусть в некотором изолированном объеме есть газ. Если температура в некоторый момент времени разная, то через некоторое время она выровнится и газ перейдет в стационарное состояние, где P, V, T – параметры. Состояние, где характеризующееся параметрами P, V, T, называется макроскопическим.
б) Микроскопическое. Состояние газа, характеризуемое положением и скоростями всех его частиц называется микроскопическим. Если в системе имеется n частиц, то в n-величин характеризуется его микроскопическое состояние. n=2,7*1019 см-3. Связь между а) и б): Каждому макроскопическому состоянию соответствует громадное количество микроскопических состояний.
Задача:(наша задача б)
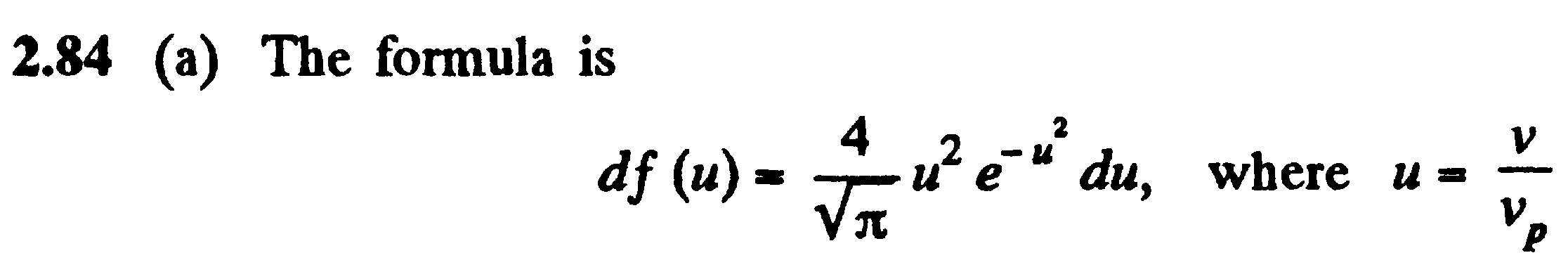 (prob – исследовать)
(prob – исследовать)
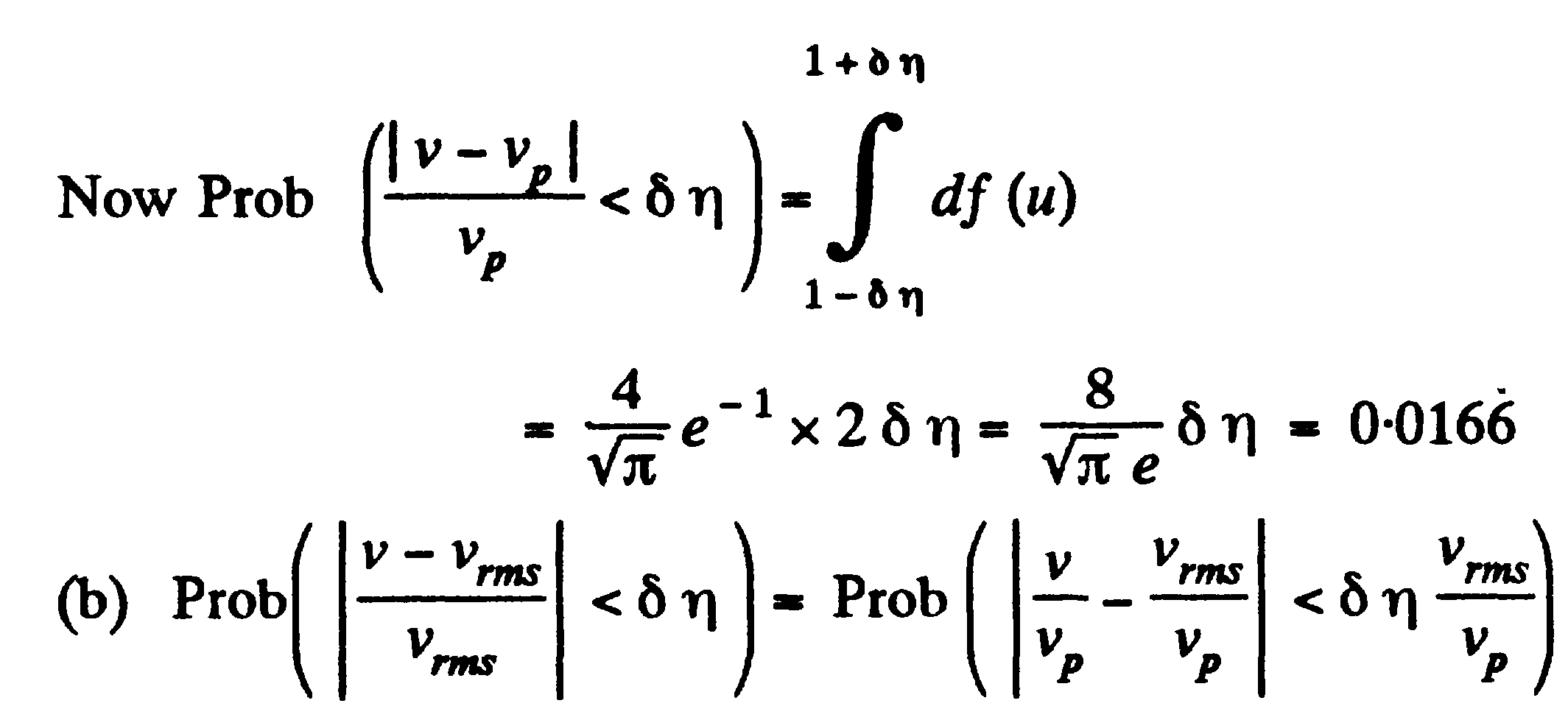 à
à 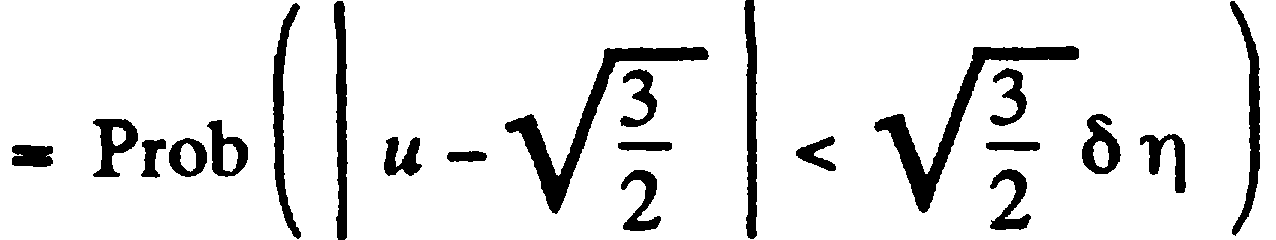 à
à 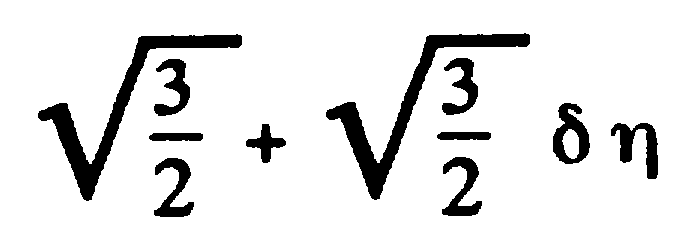
è 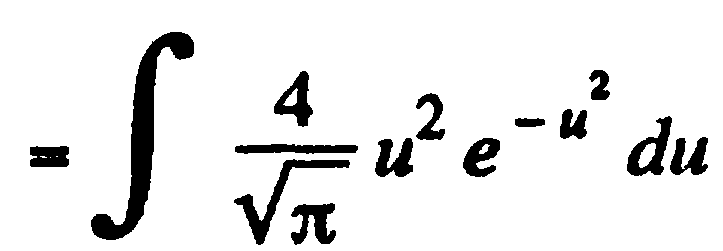 à
à 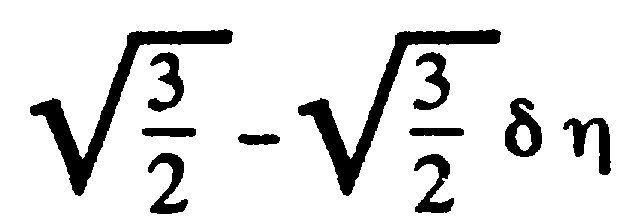 à
à 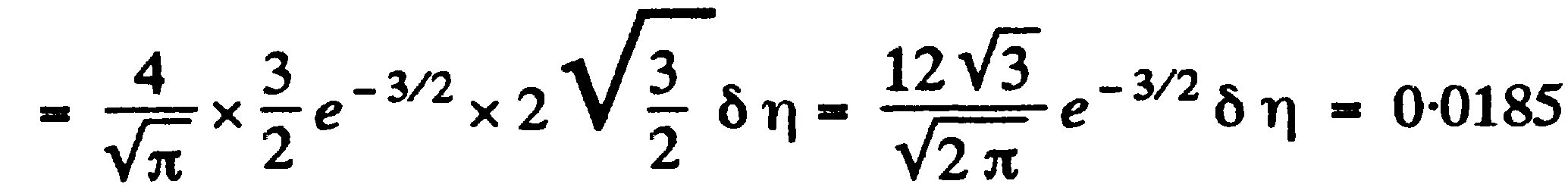
Билет №19.
Барометрическая формула.
Разность давлений p и p+dp равна весу газа, заключенного в объеме цилиндра высотой dh с основанием площадью 1 м2: 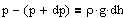
где r- плотность газа на высоте h (dh насолько мало, что при изменении высоты в этом пределе плотность газа можно считать постоянной). Следовательно, 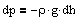
Воспользовавшись уравнением состояния идеального газа pV=(m/M)RT (m - масса газа, M - молярная масса газа), находим, что 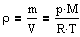
Подставим плотность и получим 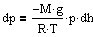 à
à 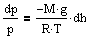
С изменением высоты от h1 до h2 давление изменяется от p1 до p2 т.е.
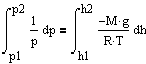 à
à 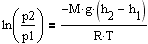 à
à 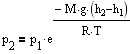 - барометрическая формула.
- барометрическая формула.
Так как высоты обозначаются относительно уровня моря, где давление считается нормальным, то выражение может быть записано в виде 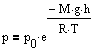
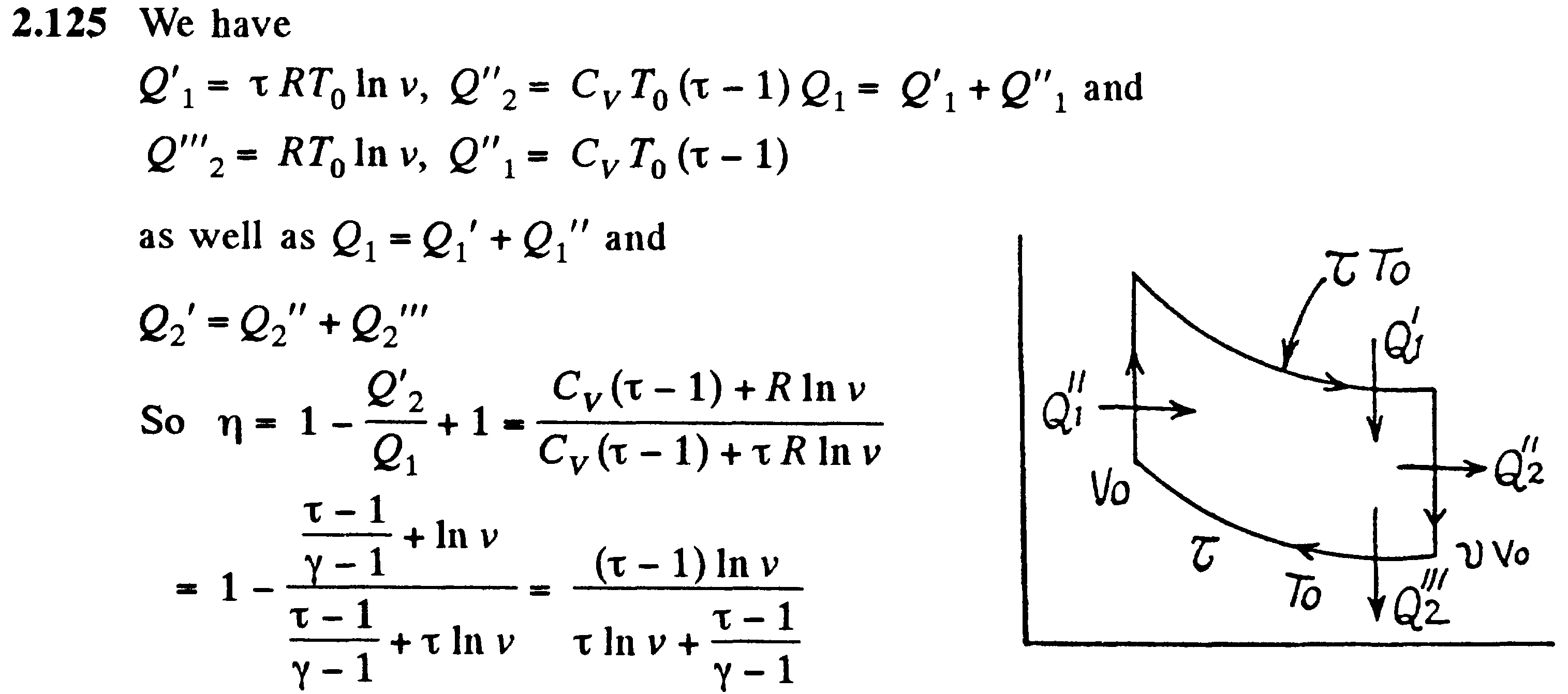
Билет №20.
Билет №21.
Число степеней свободы молекулы. Закон распределения по степеням свободы.
Степень свободы - это число независимых координат, полностью определяющих положение системы в пространстве.
Независимо от общего числа степеней свободы молекул три степени свободы всегда поступательные. Ни одна из поступательных степеней свободы не имеет преимущества перед другими, поэтому на каждую из них приходится в среднем одинаковая энергия, равная 1/3 значения e0
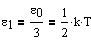
Атомы всегда находятся в движении и чем выше температура, тем интенсивнее движение. 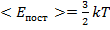 – поступательная энергия.
– поступательная энергия.
Однако наряду с поступательным движением возможны также вращательные движения и колебательные. Оба этих движения связаны с запасом энергии. Определить которую позволяет «закон о равнораспределении энергии по степеням свободы»
Числом степени свободы механической системы называется – количество независимых величин с помощью которых может быть задано положение системы. У материальной точки ч.с.с.=3, у 2-х материальных точек = 6, если они связаны, то ч.с.с.=5.
Закон Больцмана о распределении энергии по степеням свободы молекул: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится среднекинетическая энергия, равная kT/2, а на каждую колебательную степень свободы - в среднем энергия, равная kT.
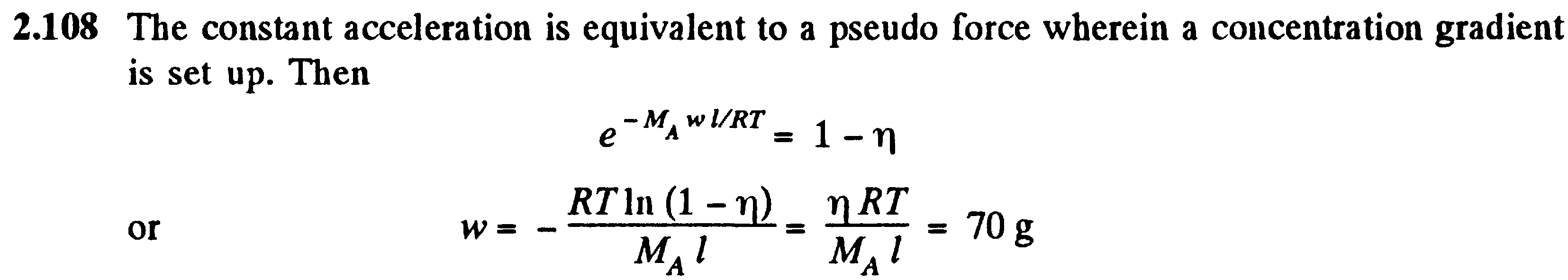
Постоянное ускорение эквивалентно псевдо силе, в чем градиент концентрации есть множество. Тогда...
Билет №22.
Модель идеального газа. Термодинамический и статистический методы.
Число Авагадро – число атомов или молекул содержащихся в 1 моле вещества. NA=6.022*1023 моль-1
Идеальный газ – газ, состоящий из молекул, взаимодействие между которыми пренебрежимо мало. Средняя кинетическая энергия молекул идеального газа во много раз больше потенциальной энергии взаимодействия. 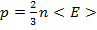 - основное уравнение для МКТ.
- основное уравнение для МКТ.
Методы:а) динамический метод n=2,7*1019 см-3 Этот метод не пригоден теоретически и практически.
б) Термодинамический метод. Теория здесь базируется на законах начала.
в) Статистический. Основан на модельных атомно-молекулярных представлениях. Задача: зная законы поведения частиц, из которых состоит система установить закон поведения макроскопического вещества.
А так же газ, удовлетворяющий этим 6 условиям, называется идеальным:
1) Закон Авагадро: При одинаковых p и T молярные объемы газов одинаковы.
2) Закон Бойля-Мариотта: При T=const pV=const
3) Закон Гей-Люссака: При p=const V/T = const
4) Закон Шарля: При V=const p/T=const
5) Закон Дальтона: общее давление равно сумме парциальных давлений.
6) Закон Джоуля: DU=CDT
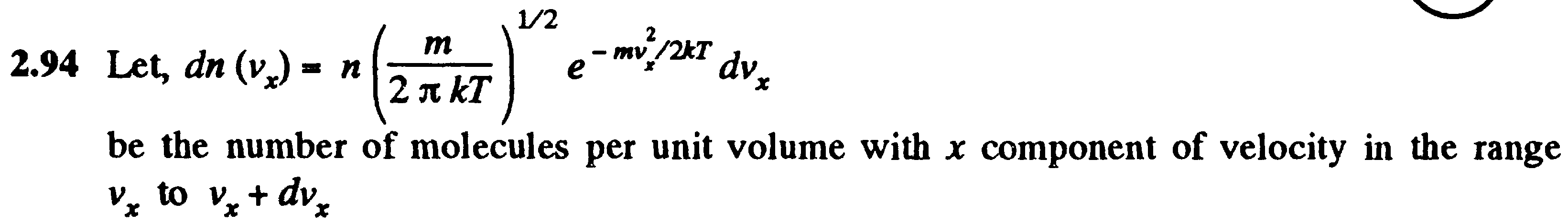
Тогда 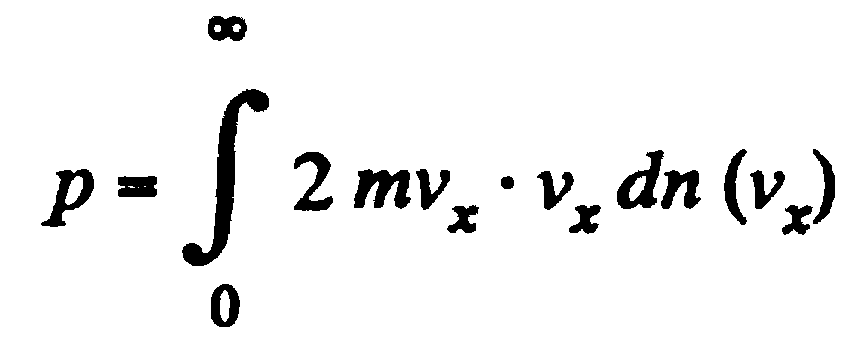 à
à 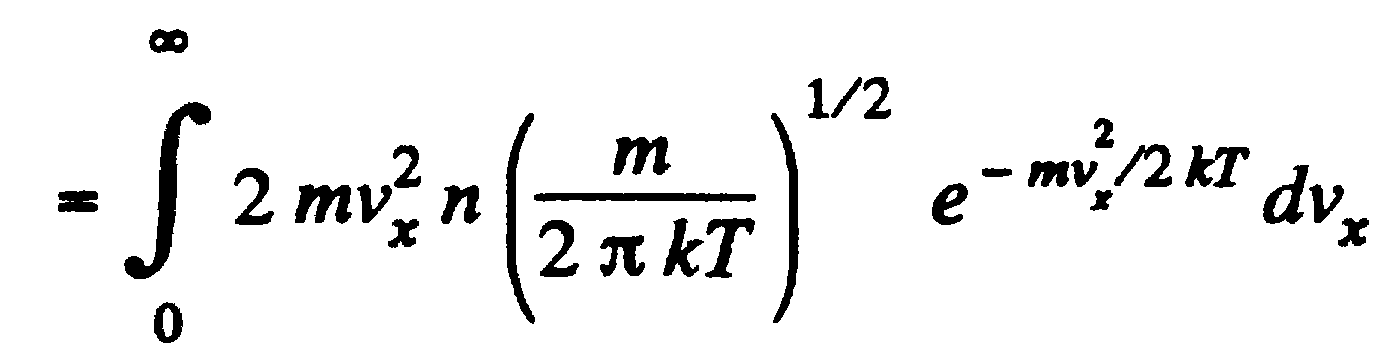 à
à 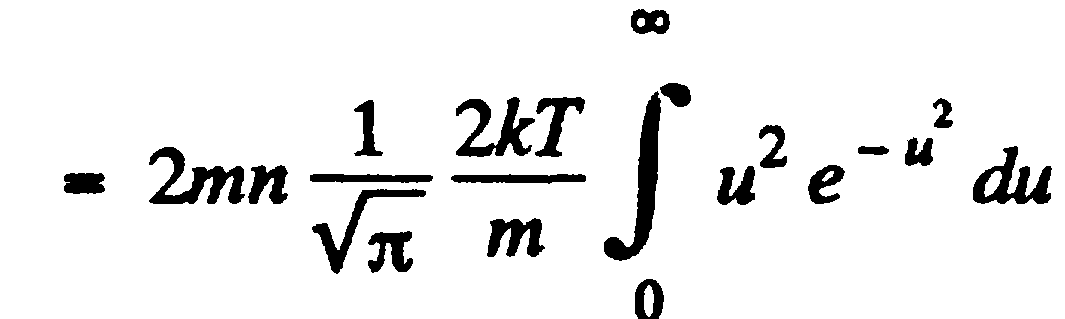 à
à 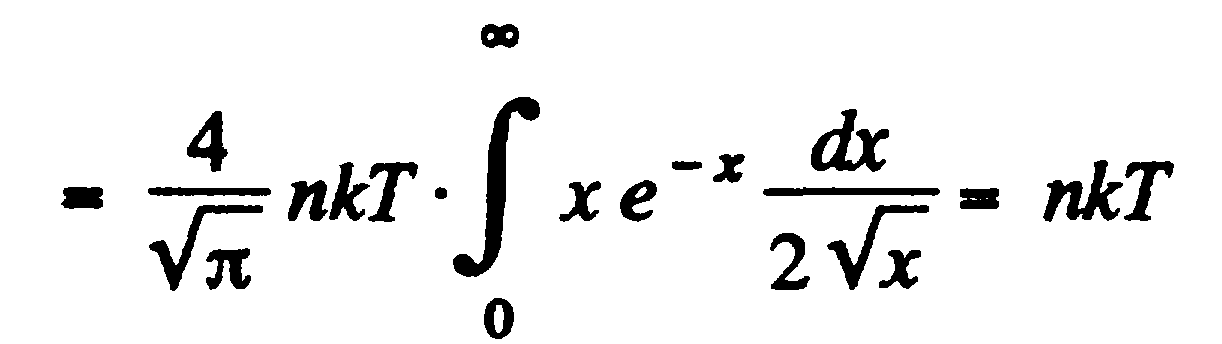
Билет №23.
Основное уравнение молекулярно-кинетической теории идеальных газов
ДЛя вывода основного уравнения молекулярно-кинетической теории рассмотрим одноатомный идеальный газ. Предположим, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие. Выделим на стенке сосуда некоторую элементарную площадку DS и вычислим давление, оказываемое на эту площадку. При каждом соударении молекула, движущаяся перпендикулярно площадке передает ей импульс m0v-(-m0v)=2m0v, где m0 - масса молекулы, v - ее скорость. За время Dt площадки DS достигнут только те молекулы, которые заключены в объеме цилиндра с основанием DS и высотой vDt. Число этих молекул равно nDSvDt. Так как молекулы движутся хаотично вдоль 3-х осей, по 6-ти направлениям, то число ударов молекул вдоль данного направления о площадку DS будет nDSvDt/6. Пр
