Для замкнутой системы тел полная механическая энергия остаётся постоянной, если в системе совершают работу только консервативные силы

4. Механические колебания и волны

Механические колебания – периодически повторяющиеся движения материальной точки по какой-либо траектории, которую эта точка проходит поочерёдно в противоположных направлениях (движения тел, повторяющиеся точно или приблизительно через одинаковые промежутки времени).

Полные колебания – один законченный цикл колебательного движения, после которого оно повторяется в том же порядке.

Виды колебаний
Собственные –	Свободные (затухающие) –	Вынужденные (незатухающие)–
колебания тела, совершаемые под действием только возвращающей силы (на практике не происходят)	колебания тела, совершаемые под действием силы сопротивления среды и возвращающей силы (груз на пружине; шарик на нити)	колебания тела, совершаемые под действием внешней силы. (резец станка, поршень автомобиля, игла швейной машины)

Параметры колебаний:

Период колебаний (Т, с)– минимальный интервал времени, через который происходит повторение движения тела, т.е. совершается одно полное колебание.

Т =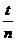

Частота колебаний (v, Гц)– число полных колебаний в единицу времени.

= ; =

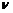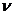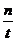
Амплитуда колебаний (А, м) – максимальное (по модулю) отклонение колеблющегося тела от положения равновесия.

Смещение (х, м) – положение колеблющегося тела в выбранный момент времени относительно положения равновесия (расстояние от положения равновесия до положения в заданный момент времени).

х = А sinφ_; х = А sin(φ₀ + ωt); х = А sin(φ₀ + 2πνt)

Фаза (φ) – число, показывающее какая часть периода прошла от момента начала колебания тела (характеризует положение и направление движения в заданный момент времени).

φ = φ₀ + ωt

Циклическая частота(ω) – число колебаний, происходящих за 2π с.

ω = 2πν = 2π/Т

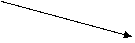
Резонанс – явление возрастание амплитуды установившихся вынужденных колебаний до максимального значения при приближении частоты изменения внешней силы к частоте свободных колебаний системы.

Маятники:

Математический маятник – материальная точка, подвешенная на невесомой и нерастяжимой нити.

Свойства математического маятника формулируют в виде двух законов:

ü При малых углах размаха период колебаний математического маятника не зависит на от амплитуды, ни от массы маятника.

ü Период колебаний математического маятника зависит от длины и ускорения свободного падения, т.е. период прямо пропорционален корню квадратному из длины маятника и обратно пропорционален корню квадратному из ускорения свободного падения: Т = 2π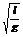

Физический маятник – тело, размерами которого нельзя пренебречь по сравнению с расстоянием от точки подвеса до центра тяжести.

Колебания физического маятника можно представить себе как совместное колебание множества материальных точек, связанных между собой, т.е. множества математических маятников с разной длиной.

Период колебаний для физического маятника:

Т = 2π ,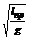

где l_пр – приведенная длина, т.е. длина математического маятника, у которого период колебаний равен периоду колебаний физического маятника.

Пружинный маятник – тело, совершающее упругие колебания (груз на пружине).

Упругие колебания – колебания, при которых возвращающая сила создаётся силами упругости.

Т = 2π 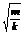– период колебания пружинного маятника

W = 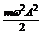– полная энергия колеблющегося тела на пружине

Волна – процесс распространения колебаний в пространстве.

ВОЛНЫ
поперечные	продольные
волны, в которых колебания происходят перпендикулярно направлению распространения (возможны только в твёрдых телах и на поверхностях жидкостей)	волны, в которых колебания происходят вдоль направления распространения (возможны в твёрдых телах, жидкостях и газах)

Волновая поверхность – непрерывное геометрическое место точек волны, колеблющихся в одинаковых фазах.

Перемещение волновой поверхности характеризуется диной волны.

Длина волны (λ, м) – расстояние между двумя ближайшими точками бегущей волны, которые колеблются в одинаковой фазе.

λ = υТ; λ = ,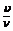

где υ – скорость распространения волны, Т – период колебаний, ν – частота колебаний

Скорость волны (υ, м/с) – скорость распространения колебаний в упругой среде

Звуковые волны.

Звук может распространяться в газах, жидкостях и твёрдых телах. В различных средах звук распространяется с различной скоростью. Скорость распространения звука в газе примерно равна скорости теплового движения молекул, с понижением температуры газа скорость распространения звука уменьшается. Связь между атомами и молекулами в жидкостях и твердых телах значительно более жесткая, чем в газах, поэтому скорость распространения в них значительно больше скорости звука в газах.