Аналогия между уравнениями поступательного и вращательного движений
Между движением твердого тела вокруг неподвижной оси и движением отдельной материальной точки (или поступательным движением тела) существует тесная и далеко идущая аналогия. Каждой линейной величине из кинематики точки соответствует подобная величина из кинематики вращения твердого тела. Координате s соответствует угол φ , линейной скорости v - угловая скорость w , линейному (касательному) ускорению а - угловое ускорение ε . Масса – Момент инерции. Импульс – Момент импульса. Сила – Момент силы. И т.д.
Сравнительные параметры движения:
Выражения для вращательного движения напоминают соответствующие выражения поступательного движения. Они получаются из последних формальной заменой m → I , v → w , p → LВыражения имеют не просто формальное сходство.
Поступательное движение можно рассматривать, как вращательное, с радиусом вращения, стремящимся к бесконечности, и угловой скоростью, стремящейся к нулю.Представленная таблица не может претендовать на всю полноту охвата аналогичных значений.
Для вращательного и поступательного движений формулируются и аналогичные законы:
Закон сохранения импульса (ЗСИ ) 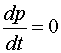 ,при Fвнеш = 0 ,при Fвнеш = 0 | Закон сохранения момента импульса (ЗСМИ ) 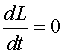 , при Mвнеш = 0 , при Mвнеш = 0 |
Эти законы формулируются следующим образом:
| «Если геометрическая сумма внешних сил, действующих на систему, равна нулю, то импульс системы сохраняется, т.е. не меняется со временем. В частности, это имеет место, когда система замкнута» | «Если момент внешних сил относительно неподвижного начала О равен нулю, то момент импульса системы относительно того же начала остается постоянным во времени» |
Перейдем к доказательству закона сохранения импульса. Допустим, что механическая система замкнута. Все силы F1 , F2 , ..., действующие на материальные точки системы, являются силами внутренними, внешних сил нет. Перенесем систему из произвольного положения 1 в другое произвольное положение 2, чтобы все материальные точки ее претерпели одно и то же смещение r, и притом так, чтобы их скорости остались прежними по величине и направлению. Ввиду однородности пространства, на такое перемещение не требуется затраты работы. Но эта работа представляется скалярным произведением (F1 +F2 + ...)r . Значит, оно равно нулю, каково бы ни было смещение r. Отсюда следует, что для замкнутой системы F1 +F2 + ...=0. А это есть как раз то условие, при выполнении которого из второго закона Ньютона получается закон сохранения импульса.
Закон сохранения момента импульса для замкнутой системы доказывается в точности так же. Используя изотропию пространства, можно доказать, что геометрическая сумма моментов внутренних сил, действующих в системе, равна нулю: М1 +М2 +...=0. Отсюда немедленно следует рассматриваемый закон. Как видно, доказательства очень похожи.
Сложное поступательно-вращательное движение тела. Мгновенная ось вращения
Поступательное движение — это механическое движение системы точек (тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени. В общем случае поступательное движение происходит в трёхмерном пространстве, но его основная особенность — сохранение параллельности любого отрезка самому себе, остаётся в силе.
Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна. В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения — когда материальная точка движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух системах отсчета. Поступательно-вращательное движение – например движение пули. Мгновенная, у твёрдого тела, имеющего неподвижную точку (например, гироскопа), проходящая через эту точку ось, поворотом вокруг которой тело перемещается из данного положения в положение к нему бесконечно близкое; движение тела за конечный промежуток времени слагается из последоват. поворотов вокруг мгновенных О. в., непрерывно изменяющих своё направление в пространстве. Движение свободного твёрдого тела в общем случае слагается из поступательного движения вместе с его центром тяжести (или др. произвольно выбранной точкой, называемой полюсом) и элементарных поворотов вокруг мгновенных О. в., проходящих через этот центр (полюс).
Законы Ньютона
Законы Ньютона образуют основу динамики — раздела механики, рассматривающего взаимодействие тел.
Первый закон Ньютона отражает свойство инерции, тел и часто называется законом инерции. Он утверждает, что всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние. Ясно, во-первых, что этот закон выполняется только в инерциальных системах отсчета. Во-вторых, отсюда следует важное заключение, что, поскольку изменение состояния покоя или равномерного движения связано с наличием в системе ускорения, последнее, в свою очередь, возникает как результат воздействия других тел. Это утверждение создает предпосылки для формулирования второго закона Ньютона.
Воздействие одного физического тела на другое характеризуется физической величиной, называемой силой. Сила, действующая на тело, сообщает ему ускорение. Величина полученного ускорения пропорциональна приложенной силе. Но разные тела под влиянием одинаковых сил приобретают разные ускорения. Данный опытный факт есть проявление уже упоминавшегося свойства инерции тела. Это свойство количественно характеризуется инертной массой тела — коэффициентом пропорциональности между приложенной к телу силой и полученным им ускорением.
Таким образом, второй закон Ньютона может быть записан в форме:
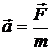 ,
, 
где фигурируют вновь введенные физические величины: вектор силы F и инертная масса тела m. В таком виде его можно сформулировать следующим образом: ускорение, приобретаемое телом, прямо пропорционально силе, действующей на тело, и обратно пропорционально массе тела. Третий закон Ньютона имеет дело со взаимодействующими, телами.
F12 = F21 m1a1=-m2a2 F1=-F2
 Он утверждает, что силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению. Важно подчеркнуть, что силы, о которых идет речь, приложены к разным взаимодействующим друг с другом телам.
Он утверждает, что силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению. Важно подчеркнуть, что силы, о которых идет речь, приложены к разным взаимодействующим друг с другом телам.
