Переходные процессы в цепях постоянного тока с конденсатором

Ознакомьтесь с теорией в конспекте и в учебниках 1. Трофимова Т.И. Курс физики. Гл.11, §94. 2. Детлаф А.А., Яворский Б.М. Курс физики. Гл.16, §16.3. Выберите: «ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ» и «Конденсаторы в цепях постоянного тока». Нажмите кнопку с изображением страницы во внутреннем окне. Прочитайте теорию и запишите основные сведения в свой конспект лабораторной работы. Закройте окно теории, нажав кнопку с крестом в правом верхнем углу внутреннего окна.

ЦЕЛЬ РАБОТЫ:

· Знакомство с компьютерным моделированием переходных процессов в цепях постоянного тока.

· Экспериментальное определение ёмкости конденсатора.

КРАТКАЯ ТЕОРИЯ:

ПЕРЕХОДНЫМ ПРОЦЕССОМ называется процесс перехода от одного установившегося в цепи режима к другому. Примером такого процесса является зарядка и разрядка конденсатора. В ряде случаях законы постоянного тока можно применять и к изменяющимся токам, когда изменение тока происходит не слишком быстро. В этих случаях мгновенное значение силы тока будет практически одно и то же во всех поперечных сечениях цепи. Такие токи называют квазистационарными

РАЗРЯДКА КОНДЕНСАТОРА. Если обкладки заряженного конденсатора ёмкости С замкнуть через сопротивление R, то через это сопротивление потечёт ток. Согласно закону Ома для однородного участка цепи

IR=U,

где I и U – мгновенные значения силы тока в цепи и напряжения на обкладках конденсатора. Учитывая, что и , преобразуем закон Ома к виду

(1)

В этом дифференциальном уравнении переменные разделяются, и после интегрирования получим закон изменения заряда конденсатора со временем

, (2)

где q₀ - начальный заряд конденсатора, е - основание натурального логарифма. Произведение RC, имеющее размерность времени, называется время релаксации t . Продифференцировав выражение (2) по времени, найдём закон изменения тока:

, (3)

где I₀ - сила тока в цепи в момент времени t = 0. Из уравнения (3) видно, что t есть время, за которое сила тока в цепи уменьшается в е раз.

МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:

1.Соберите на рабочей части экрана замкнутую электрическую цепь, показанную на рис. 1

Рис.1

Для этого сначала щёлкните мышью на кнопке э.д.с., расположенной в правой части окна эксперимента. Переместите маркер мыши на рабочую часть экрана, где расположены точки, и щёлкните маркером мыши в виде вытянутого указательного пальца в том месте, где должен быть расположен источник тока. Подведите маркер мыши к движку появившегося регулятора э.д.с., нажмите на левую кнопку мыши, удерживая её в нажатом состоянии, меняйте величину э.д.с. и установите 10 В. Аналогичным образом включите в цепь 4 других источника тока. Суммарная величина э.д.с. батареи должна соответствовать значению, указанному в таблице 1 для вашей бригады. Таким же образом разместите далее на рабочей части экрана 7 ламп Л1-Л7 ( кнопка ), ключ К (кнопка ), вольтметр (кнопка ), амперметр (кнопка ), конденсатор (кнопка ). Все элементы электрической цепи соедините по схеме рис.1 с помощью монтажных проводов (кнопка ).

2. Щёлкните мышью на кнопке «Старт». Должна засветиться лампа Л7, а надпись на кнопке измениться на «Стоп». Курсором мыши замкните ключ К.

3. После установления в цепи стационарного тока ( должны погаснуть лампы Л5 и Л6 и светиться лампы Л1-Л4) запишите показания электроизмерительных приборов. в таблицу 2

4. Нажмите на кнопку «Стоп» и курсором мыши разомкните ключ К.

5. Двумя короткими щелчками мыши на кнопке «Старт» запустите и остановите процесс разрядки конденсатора. Показания амперметра будут соответствовать начальному току разрядки конденсатора I₀. Запишите это значение в таблицу 3.

6. Вновь замкните ключ, зарядите конденсатор и повторите п.п. 5,6 ещё 4 раза.

7. Для каждого опыта рассчитайте I_t= I₀/2,7- силу тока, которая должна быть в цепи разрядки конденсатора через время релаксации t и запишите эти значения в таблицу 3.

8. При разомкнутом ключе нажатием кнопки «Старт» запустите процесс разрядки конденсатора и одновременно включите секундомер.

9. Внимательно наблюдайте за изменением показаний амперметра в процессе разрядки конденсатора. Остановите секундомер и синхронно нажмите кнопку «Стоп» при показании амперметра, равном или близким к I_t. Запишите это значение времени t₁ в таблицу 3.

10. Проделайте опыты п.п.8, 9 ещё 4 раза.

Таблица 1. Суммарное значение э.д.с. батареи 5 источников тока.

Бригада
Э.д.с.,В

Таблица 2. Определение сопротивления лампы.

I, А	U, В	R, Ом

Таблица 3. Результаты измерений и расчётов.

Номер опыта						Среднее значение
I0, А
It, А
t, с
C, Ф

ОБРАБОТКА РЕЗУЛЬТАТОВ:

1.По закону Ома для участка цепи Л1-Л4: и результатам измерений, приведённым в таблице 2, определите сопротивление одной лампы.

2. По формуле (при разрядке конденсатора квазистационарный ток протекает по 6 последовательно соединённым лампам) определите ёмкость конденсатора и запишите эти значения в таблицу 3.

3. Рассчитайте погрешности измерений и сформулируйте выводы по результатам проделанной работы.

Вопросы и задания для самоконтроля

1. Что представляет собой конденсатор и от чего зависит его ёмкость?

2. Выведите формулы ёмкости плоского, цилиндрического и сферического конденсаторов.

3. Как изменяется разность потенциалов на обкладках конденсатора при его зарядке и разрядке?

4. Какой ток называется квазистационарным?

5.Выведите формулы электроёмкости батареи последовательно и параллельно соединённых конденсаторов

6. Что такое время релаксации?

7. Объясните принцип работы экспериментальной установки.

ЛАБОРАТОРНАЯ РАБОТА № 9

МАГНИТНОЕ ПОЛЕ

Ознакомьтесь с конспектом лекций и учебником (Савельев, т.2, §39-47). Запустите программу «Эл-магн.Кванты». Выберите «Электричество и магнетизм» и «Магнитное поле прямого тока». (Если вы забыли, как работать с системой компьютерного моделирования, прочитайте ВВЕДЕНИЕ стр.5 еще раз).

Нажмите вверху внутреннего окна кнопку с изображением страницы. Прочитайте краткие теоретические сведения. Необходимое запишите в свой конспект. Закройте внутреннее окно, нажав кнопку с крестом справа вверху этого окна, и вызовите сначала эксперимент «Магнитное поле витка с током», а затем «Магнитное поле соленоида». Прочитайте и запишите в свой конспект необходимые краткие теоретические сведения.

ЦЕЛЬ РАБОТЫ

* Знакомство с моделированием магнитного поля от различных источников.

* Экспериментальное подтверждение закономерностей для магнитного поля прямого провода и кругового витка (контура) с током.

* Экспериментальное определение величины магнитной постоянной.

КРАТКАЯ ТЕОРИЯ

Магнитным полем (МП) называется область пространства, в которой на электрически нейтральный проводник с током действует сила, называемая магнитной. Источником МП является движущаяся электрически заряженная частица (заряд), которая создает также и электрическое поле.

Если вблизи одной движущейся заряженной частицы (заряда №1) будет находиться вторая движущаяся с такой же скоростью V заряженная частица (заряд №2), то на второй заряд будут действовать 2 силы: электрическая (кулоновская) и магнитная сила , которая будет меньше электрической в раз, где с – скорость света.

Для практически любых проводов с током выполняется принцип квазинейтральности: несмотря на наличие и движение заряженных частиц внутри проводника, любой (не слишком малый) его отрезок имеет нулевой суммарный электрический заряд. Поэтому между обычными проводами с током наблюдается только магнитное взаимодействие.

магнитная индукция - характеристика силового действия МП на проводник с током, векторная величина, обозначаемая символом .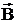

линии магнитной индукции - линии, в любой точке которых вектор индукции МП направлен по касательной.

Анализ взаимодействия движущихся зарядов с учетом эффектов теории относительности (релятивизма) дает выражение для индукции МП, создаваемого элементарным отрезком c током I , расположенным в начале координат (закон Био-Савара-Лапласа или Б-С-Л):

,

где - радиус-вектор точки наблюдения, - единичный радиус-вектор, направленный в точку наблюдения, m₀ - магнитная постоянная.

МП подчиняется принципу суперпозиции: индукция МП нескольких источников является суммой индукций полей, создаваемых независимо каждым источником .

Циркуляцией МП называется интеграл по замкнутому контуру от скалярного произведения индукции МП на элемент контура: .

Закон циркуляции МП: циркуляция МП по замкнутому контуру L₀ пропорциональна суммарному току, пронизывающему поверхность S(L₀), ограниченную этим контуром L₀ .

Закон Б-С-Л и принцип суперпозиции МП позволяют получить многие другие закономерности, в частности, индукцию магнитного поля прямого бесконечно длинного проводника с током: .

Линии магнитной индукции поля прямого проводника с током представляют собой концентрические окружности, лежащие в плоскостях, перпендикулярных проводнику, с центрами, расположенными на его оси.

Индукция МП на оси кругового контура (витка) радиуса R с током I на расстоянии r от центра: ,

где - магнитный момент витка площадью S, - единичный вектор нормали к поверхности витка.

Соленоидом называется длинная прямая катушка с током. Величина индукции МП вблизи центра соленоида меняется очень мало. Такое поле можно считать практически однородным.

Из закона циркуляции МП можно получить формулу для индукции МП в центре соленоида B = m₀In , где n – число витков, приходящихся на единицу длины соленоида.