Теорема остроградского -гаусса для электростатического поля в вакууме
Ознакомьтесь с теорией в конспекте и в учебниках: 1. Трофимова Т.И. Курс физики. Гл. 11, §81,82; 2. Детлаф А.А., Яворский Б.М. Курс физики. Гл. 14,§ 14.1, 14.2. Запустите программу «Открытая физика 1.1». Выберите «Электричество и магнетизм» и «Электрическое поле точечного заряда». Нажмите вверху внутреннего окна кнопку с изображением страницы. Прочитайте краткие теоретические сведения. Необходимое запишите в свой конспект. (Если вы забыли, как работать с системой компьютерного моделирования, прочитайте ВВЕДЕНИЕ стр.5 еще раз).
ЦЕЛЬ РАБОТЫ:
· Знакомство с графическим моделированием электростатических полей.
· Экспериментальная проверка теоремы Остроградского-Гаусса.
· Экспериментальное определение величины электрической постоянной.
КРАТКАЯ ТЕОРИЯ:
НАПРЯЖЁННОСТЬ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ в данной точке есть векторная физическая величина, равная отношению силы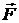 
, действующей со стороны поля на неподвижный точечный заряд q0, помещённый в данную точку поля, к величине этого заряда:
.
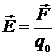ЛИНИЯМИ НАПРЯЖЁННОСТИ (силовыми линиями) называются линии, проведённые в поле так, что касательные к ним в каждой точке совпадают по направлению с вектором напряжённости. Линии напряжённости проводят так, что они начинаются на положительных зарядах и оканчиваются на отрицательных или уходят в бесконечность. (Рис. 1)
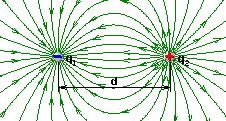
а) б)
Рис.1. Линии напряжённости двух точечных зарядов: а) разноимённых;
б) одноимённых
ПРИНЦИП СУПРПОЗИЦИИ ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ: напряжённость электростатического поля систем точечных зарядов равна векторной сумме напряжённостей полей каждого из этих зарядов в отдельности:
.
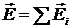ПОТОК ВЕКТОРА НАПРЯЖЁННОСТИ.
Силовая линия, определяя направление вектора напряжённости, сама по себе не определяет величину модуля вектора напряжённости. Введём условие, связывающее величину модуля вектора напряжённости с числом проводимых линий напряжённости через единицу площади. Для этого выделим в электростатическом поле малую область, в пределах которой электростатическое поле можно считать однородным. Проведём в этой области элементарную площадку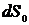 
, перпендикулярную к линиям напряжённости. Условимся через эту площадку проводить такое число 
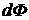линий напряжённости, чтобы число линий, приходящихся на единицу поверхности площадки 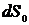, равнялось величине модуля вектора напряжённости в области этой площадки, т.е. потребуем выполнения условия:
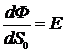. (1)
При выполнении этого условия графического изображения электростатических полей численное значение вектора напряжённости будет связано с густотой линий напряжённости. Тогда число линий напряжённости, пронизывающих элементарную площадку dS, нормаль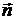 
которой образует угол a с вектором 
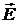, равно
, (2)
где величина dФ называется потоком вектора напряжённости через площадку dS. Число линий напряжённости Ф, пронизывающих некоторую поверхность S, назовём потоком вектора напряжённости через эту поверхность. Для произвольной замкнутой поверхности S поток вектора Е сквозь эту поверхность будет равен
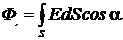. (3)
Для замкнутой поверхности принято считать положительным направление нормали к элементу поверхности, выходящее из объёма, ограничиваемого поверхностью. Тогда линии напряжённости, выходящие из объёма, создадут положительный поток Ф+, линии, входящие в объём, создадут отрицательный поток Ф-, а результирующий поток будет равен алгебраической сумме этих потоков.
ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА: поток вектора напряжённости электростатического поля в вакууме через произвольную замкнутую поверхность равен алгебраической сумме заключённых внутри этой поверхности зарядов, делённой на e0.
Ф+ + Ф- =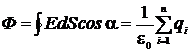 
(4)
МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:
Рассмотрите внимательно схему опыта и зарисуйте необходимое в свой конспект лабораторной работы.
Рис. 2
Как известно, электростатическое поле в вакууме изотропное. Следовательно, количество силовых линий, пересекающих произвольную замкнутую поверхность, содержащую внутри себя электрические заряды, будет пропорционально количеству силовых линий, пересекающих замкнутый контур, ограничивающий площадь сечения, в которой находятся электрические заряды этой замкнутой поверхности.
Такое допущение даёт возможность привести в количественное соответствие реальное трёхмерное электростатическое поле с его графической интерпретацией в плоской компьютерной модели, которая показана на рис. 2. Для этого определим число силовых линий Ф, которые фактически должны пересекать произвольную замкнутую поверхность, внутри которой находится электрический заряд q = 1мкКл. По теореме Остроградского-Гаусса имеем:
.
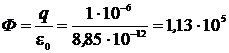Откройте окно опыта. В нижнем правом прямоугольнике «Конфигурация» щёлкните мышью на кнопке «Один заряд». Зацепив мышью, перемещайте движок регулятора величины заряда и установите значение q1 = +1мкКл. Подсчитайте число силовых линий, выходящих из заряда. Их должно быть 6. Следовательно, силовая линия в плоской компьютерной модели опыта соответствует
N =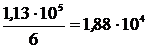 
(5)
линиям реального трёхмерного кулоновского поля. На основании таких допущений и оценок создаётся возможность экспериментальной проверки теоремы Остроградского-Гаусса с помощью графического компьютерного моделирования электростатических полей в данной лабораторной работе.
ЭКСПЕРИМЕНТ 1. (Постоянное пространственное распределение переменного заряда внутри замкнутой поверхности)
1. В нижнем правом прямоугольнике «Конфигурация» нажмите мышью кнопку «Два заряда».
2. Зацепив мышью, перемещайте движок регулятора первого заряда до установления значения, указанного в табл. 1 для вашей бригады.
3. Аналогичным образом установите заданное в табл.1 расстояние d между зарядами.
4. Установите мышью на кнопке «Силовые линии» флажок.
5. Установите величину второго заряда 0 и подсчитайте число силовых линий Ф+ выходящих и Ф- входящих через границы замкнутого контура, которым в нашем опыте будет являться прямоугольная рамка окна опыта. При этом внимательно смотрите за направлением стрелок на силовых линиях поля. Запишите эти данные и разность Ф = Ф+ - Ф- в таблицу 2.
6. Последовательно устанавливайте заряды: q2 = +1, +2, +3, +4, +5мкКл и выполните п.5 ещё 5 раз.
ЭКСПЕРИМЕНТ 2.(Переменное пространственное распределение постоянного заряда внутри замкнутой поверхности)
1. Установите значения q1 и q2 соответствующие значениям, указанным в таблице 1 для вашей бригады.
2. Установите также минимальное расстояние между зарядами d = 2м и на экране окна эксперимента, подсчётом определите числа Ф+ , Ф- и Ф.
3. Последовательно увеличивая расстояние между зарядами с шагом 0,5м, выполните п. 2 ещё 6 раз.
4. Результаты измерений запишите в табл. 3.
Таблица 1. Установочные значения физических параметров для проведения экспериментов
| Бригады | ||||||||
| ЭКСПЕРИМЕНТ 1 | ||||||||
| q1,мкКл | -1 | -2 | -3 | -4 | -5 | -4 | -3 | -2 |
| d, м | ||||||||
| ЭКСПЕРИМЕНТ 2 | ||||||||
| q1,мкКл | -5 | -5 | -5 | -5 | -5 | -4 | -4 | -4 |
| q2,мкКл | +1 | +2 | +3 | +4 | +5 | +4 | +3 | +2 |
Таблица 2. Результаты измерений в эксперименте 1
q1 = _____ d =_____
| q2 = 0 мкКЛ | q2 = +1 мкКЛ | q2 = +2 мкКЛ | q2 = +3 мкКЛ | q2 = +4 мкКЛ | q2 = +5 мкКЛ | ||||||||||||
| Ф+ | Ф- | Ф | Ф+ | Ф- | Ф | Ф+ | Ф- | Ф | Ф+ | Ф- | Ф | Ф+ | Ф- | Ф | Ф+ | Ф- | Ф |
Таблица 3. Результаты измерений в эксперименте 2.
q1 = _____ q2 = ______
| d =2м | d = 3м | d = 4м | d = 5м | d =4,5 м | d =3,5 м | ||||||||||||||||||
| Ф+ | Ф- | Ф | Ф+ | Ф- | Ф | Ф+ | Ф- | Ф | Ф+ | Ф- | Ф | Ф+ | Ф- | Ф | Ф+ | Ф- | Ф | ||||||
ОБРАБОТКА РЕЗУЛ ЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЁТА
1. Постройте по данным табл.2 график зависимости потока вектора напряжённости Ф от величины заряда q.
2. По котангенсу угла наклона графика и используя ф-лы (4) и (5), определите электрическую постоянную e0 .
3. По данным, приведённым в табл.3, постройте график зависимости потока вектора напряжённости Ф от расстояния между зарядами d.
4. По построенным графикам сделайте анализ результатов и оцените погрешность проведённых измерений.
Вопросы и задания для самоконтроля
1. Какие поля называют электростатическими?
2. Что такое напряжённость электростатического поля?
3. Как определяется направление вектора напряжённости?
4. Что такое поток вектора напряжённости?
5. Какая линия называется силовой? Почему они не могу пересекаться?
6. Какая линия называется эквипотенциальной?
7. Докажите, что эквипотенциальные и силовые линии ортогональны.
8. От чего зависит густота силовых и эквипотенциальных линий?
9. В чём заключается физический смысл теоремы Остроградского-Гаусса?
10. Рассчитайте, используя теорему О-Г,
а) поле равномерно заряженной бесконечной плоскости;
б) поле двух бесконечных параллельных разноимённо заряженных плоскостей;
в) поле равномерно заряженной сферической поверхности;
г) поле объёмно заряженного шара;
д) поле равномерно заряженного бесконечного цилиндра (нити);
11. Каким образом теорема О-Г и следствия из неё могут быть косвенным подтверждением справедливости закона Кулона?
ЛАБОРАТОРНАЯ РАБОТА № 6