Два способа изменения внутренней энергии. Теплота и работа

Состояния термодинамической системы (т.е. и её внутренняя энергия) могут быть изменены двумя способами:

1). Путём теплообмена (конвективным способом, теплопроводностью, тепловым излучением).

2). Путём совершения механической работы.

Количество энергии, переданное системе внешними телами путём теплообмена называется количеством теплоты: (Дж).

Количество теплоты – величина скалярная и алгебраическая; принято считать: > 0 – система получает тепло; < 0 – система отдаёт тепло.

Работой А, совершаемой над системой называется количество энергии, переданное системе внешними телами при силовом взаимодействии между ними.

Работа – величина алгебраическая; принят считать: А> 0 – работа, совершаемая системой над внешней средой; А′ < 0 – работа, совершаемая над системой внешними телами; причём А′ = А.

Работа и теплота, как формы передачи энергии, качественно различны. Механическая работа может идти на изменение как внутренней энергии системы, так и её механической энергии. Энергия, сообщаемая в форме теплоты, идёт только на увеличение внутренней энергии системы.

Обратимые и необратимые процессы

В термодинамике различают обратимые и необратимые процессы.

Обратимым термодинамическим процессов называется процесс, допускающий возможность возвращения системы в первоначальное состояние без того, чтобы в окружающей среде остались какие-либо изменения.

Примеры обратимых процессов:механический процесс при отсутствии трения; упругий удар о горизонтальную плоскость. Обратимость механических движений означает их симметричность по отношению к изменению знака времени.

Необходимым условием обратимости термодинамического процесса является его равновесность (квазистатичность). Всякий обратимый процесс является равновесным, но не всякий равновесный процесс – обратимым.

Обратимый процесс является процессом идеализированным. Все реальные процессы протекают с конечной скоростью, сопровождаются трением, диффузией, теплообменом, т.е. все реальные процессы необратимые.

Необратимым термодинамическим процессом называется процесс, не допускающий возможности возвращения системы в первоначальное состояние без того, чтобы в окружающей среде остались какие-либо изменения.

Такой процесс в прямом направлении протекает самопроизвольно, а для осуществления его в обратном направлении требуется компенсирующий процесс во внешних телах, в результате которого состояние этих тел оказывается отличным от первоначальных.

Примеры необратимых процессов: процесс торможения тел под действием сил трения; процесс расширения газа в пустоту; процесс теплообмена между контактирующими телами с различной температурой и т.п.

Однако, если процесс протекает достаточно медленно (квазистатически), то степенью его необратимости можно пренебречь.

Работа расширения идеального газа. Графическое изображение работы

Рассмотрим идеальный газ, находящийся под невесомым подвижным поршнем. Процесс расширения газа будем считать квазистатическим, т.е. P = const (рис. 118).

Если газ, расширяясь, передвигает поршень на расстояние dl, то производит над ним работу: = F• dl, где F = P•S – сила давления газа на поршень. Учтем, что S• dl = dV – элементарное увеличение объёма газа под поршнем.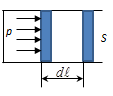

Рис. 118.

Тогда элементарная работа расширения газа под поршнем равна:

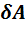= P• dV.

Полная работа, совершаемая газом при конечном изменении объёма выражается через интеграл:

A₁₂ =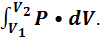

Графически можно изображать только равновесные (квазистатические) процессы.

Изменение давления газа при его расширении задаётся на рис. 119 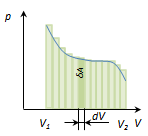произвольной кривой:

Рис. 119.

Элементарная работа 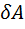численно равна площади криволинейной трапеции с основанием dV. Полная работа A₁₂ измеряется площадью всей криволинейной с основанием V₁V_2.

Из рис. 119 видно, что работа A₁₂ зависит от того, как система переходит из состояния 1 в состояние 2, т.е. от вида процесса.

Круговые процессы (циклы)

Термодинами́ческие ци́клы — круговые процессы в термодинамике, то есть такие процессы, в которых начальные и конечные параметры, определяющие состояние рабочего тела (давление, объём, температура, энтропия), совпадают (рис. 120).

Термодинамические циклы являются моделями процессов, происходящих в реальных тепловых машинах для превращения тепла в механическую работу.

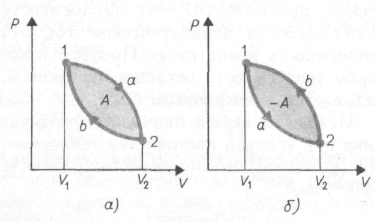
Рис. 120.

Круговым процессом (циклом) называется такая совокупность термодинамических процессов, в результате которых система возвращается в исходное состояние.

На диаграмме процессов цикл изображается замкнутой кривой.

Цикл можно разбить на процессы расширения (1 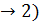и сжатия (2 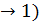газа. Работа расширения (определяется площадью фигуры 1а2V₂V₁1) положительная (∆V > 0), работа сжатия (определяется площадью фигуры 2b1V₁V₂2) отрицательная (∆V < 0). Работа за цикл определяется площадью, охватываемой замкнутой кривой. Если за цикл работа равна: A = 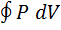> 0 (цикл описывается по часовой стрелке), то цикл называется прямым (рис. 120, а), если за цикл работа равна: A = 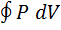< 0 (цикл описывается против часовой стрелки), то цикл называется обратным (рис. 120, б).

Так как внутренняя энергия системы зависит только от её состояния, то полное изменение внутренней энергии в цикле равно нулю (∆U = 0). Однако, полная работа в цикле не равна нулю: А₁₁ 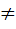0.

В прямом цикле 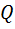> 0 и А> 0, т.е. система совершает работу за счёт сообщённой ей теплоты. В обратном цикле над системой совершается работа (А< 0 и 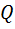< 0) и системы отводится, равное этой работе, количество теплоты.

Прямой цикл осуществляется в тепловой машине, обратный – в холодильной машине.

Вывод: работа А и количество теплоты 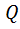не являются функциями состояния системы.

Первое начало термодинамики

Существуют две формы передачи энергии от одних тел к другим – работа и теплота. Энергия механического движения может превращаться в энергию теплового движения и наоборот. При этих превращениях соблюдается закон сохранения и превращения энергии.

Первое начало термодинамики — один из трёх основных законов термодинамики, представляет собой закон сохранения энергии для термодинамических систем. Первое начало термодинамики было сформулировано в середине XIX века в результате работ немецкого учёного Ю. Р. Майера[36], английского физика Дж. П. Джоуля и немецкого физика Г. Гельмгольца[37].