Зависимость функции распределения Максвелла от температуры.

Хотя уравнение Мааксвелла дает распределение скоростей, или, другими словами, долю молекул, имеющих специфическую скорость, часто более интересны другие величины, такие как средние скорости частиц. В следующих подразделах мы определим и получим наиболее вероятную скорость, среднюю скорость и среднеквадратичную скорость.

Характерные скорости

Наиболее вероятная скорость

Наиболее вероятная скорость, 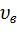— вероятность обладания которой любой молекулой системы максимальна, и которая соответствует максимальному значению f( ).

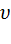Чтобы найти её, необходимо вычислить 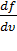, приравнять её нулю и решить

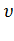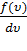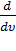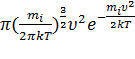относительно : = [4 ] = 0.

В итоге получим: 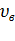= = 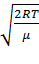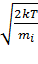, где R = 8,31 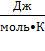– универсальная газовая постоянная, 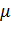– молярная масса газа, k – постоянная Больцмана, m_i – масса молекулы газа, Т – температура газа.

Средняя скорость

Подставляя f( 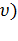и интегрируя, мы получим:

< = = => < = .

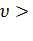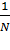
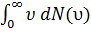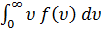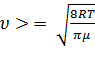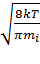Среднеквадратичная скорость

Подставляя f( 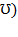и интегрируя, мы получим:

< = = .

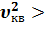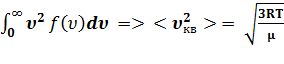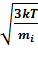Т.о., скорости, которые характеризуют состояние газа:

1) наиболее вероятная = = ,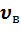

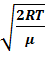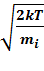2) средняя < 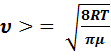= = 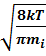1,13 ,

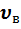3)средняя квадратичная 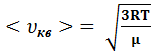= =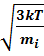1,22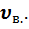

Экспериментальная проверка закона распределения Максвелла -– опыт Штерна

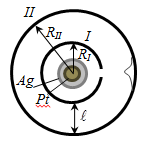Вдоль оси внутреннего цилиндра с целью натянута платиновая проволока, покрытая слоем серебра, которая нагревается током. При нагревании серебро испаряется, атомы серебра вылетают через щель и попадают на внутреннюю поверхность второго цилиндра. Если оба цилиндра неподвижны, то все атомы независимо от их скорости попадают в одно и то же место В (рис. 113).

Рис.113.

При вращении цилиндров с угловой скоростью ω атома серебра попадут в точки В’, B’’ и так далее. По величине ω, расстоянию l и смещению х = ВВ’ можно вычислить скорость атомов, попавших в точку В’.

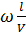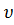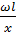x = R_II; = R_II.

Изображение щели получается размытым. Исследуя толщину осаждённого слоя, можно оценить распределение молекул по скоростям, которое соответствует максвелловскому распределению.

1.11. Основное уравнение молекулярно – кинетической теории (уравнение Клаузиуса[28])

Рассмотрим идеальный газ в равновесном состоянии, вне силовых полей внутри куба с ребром l. Давление газа на грани куба обусловлен6о ударами молекул.

Упрощённое доказательство уравнения

Молекулы движутся беспорядочно, поэтому все направления их движения равновероятны: N молекул из их общего числа N будет двигаться между каждыми двумя гранями куба.

Обозначим: m_i –масса молекулы, -–скорость молекулы, ∆t – время удара молекулы о стенку, k – количество ударов i - той молекулы о стенку за некоторое время t; - время между двумя последовательными соударениями молекулы со стенкой.

Считаем молекулы классическими частицами, удары молекул о стенку упругими. По второму закону Ньютона сила удара i – той молекулы о стенку (рис. 114): f_i = . (1)

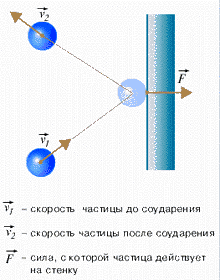
Рис. 114.

За время t молекула ударит о стенку k раз и передаст ей импульс (2m_i k).

Средняя сила, действующая на стенку со стороны i - той молекулы:

<F_i > = k , (2)

где k = = , т.к. = .

Получаем: <F_i > = .

Средняя (за время t) сила давления i – той молекулы на стенку:

<F_i> = . (3)

Т.к. разные молекулы движутся с различными скоростями, то давление со стороны всей совокупности молекул, движущихся между двумя противоположными стенками:

<F> = + + … + . (4)

Т.к. n = N – число молекул, движущихся между двумя противоположными гранями куба, то (4) примет вид:

<F> = = = ,

или <F> = |: (5)

Получим: = (6)

где l² – площадь грани куба, l³ - объём куба.

Тогда (6) примет вид: P = n₀ m_i P = n₀ , (7)

где <E_к> = – средняя кинетическая энергия поступательного движения молекул.

Тогда уравнение (7) примет вид:

P = n₀ <E_к>. (8)

Уравнение (8) – основное уравнение МКТ (уравнение Клаузиуса):

давление идеального газа прямо пропорционально концентрации молекул и средней кинетической энергии их поступательного движения.

Учтём, что . (9)

Подставив (9) в (7), получим: P= n₀ = n₀kT,

т.е. в итоге получаем: P= n₀ k T. (10)

Уравнение (10) – уравнение состояния идеального газа:

давление идеального газа пропорционально концентрации молекул газа и его абсолютной температуры.

Из уравнений (9) и (8) следует: n₀ <E_к> = n₀ k T => <E_к> = k T,

т.е. абсолютная температура является мерой средней кинетической энергии теплового поступательного движения молекул.

1.12. Уравнение Менделеева[29] - Клапейрона[30]

Уравнение Менделеева – Клапейрона -–уравнение состояния идеального газа, устанавливающее связь между его объемом V, давлением P и абсолютной температурой T.

Рассматриваем идеальный газ. Уравнение состояния идеального газа:

P = n₀ k T | V,

где V – объём газа.

Получаем: PV = n₀V kT. Учтём, что N = n₀V = N_a – число частиц газа, где -–число молей газа, N_a – постоянная Авогадро.

Тогда получаем: PV = NkT = N_a kT, где N_a k = R = 8,31 – универсальная газовая постоянная.

Окончательно получаем: PV= RT.

Последнее уравнение является уравнением состояния идеального газа и называется уравнением Менделеева – Клапейрона.

Частные случаи уравнения Менделеева – Клапейрона

Рассматриваем идеальный газ постоянной массы (m = const):

Изотермический процесс – процесс, протекающий в системе постоянной массы при постоянной температуре (T=const).

Процесс описывается законом Бойля[31]- Мариотта[32]: произведение объёма данной массы газа на его давление постоянно при постоянной температуре: PV=const.

Изобарный процесс – процесс, протекающий в системе постоянной массы при постоянном давлении (P=const).

Процесс описывается законом Гей – Люссака[33]: отношение объёма данной массы газа его абсолютной температуре при постоянном давлении есть величина постоянная:

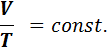
Изохорный процесс – процесс, протекающий в системе постоянной массы при постоянном объёме (V = const).

Процесс описывается законом Шарля[34] : отношение давление данной массы газа при постоянном объемё его абсолютной температуре есть величина постоянная:

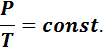
Закон Дальтона[35]

В состоянии теплового равновесия давление в смеси идеальных газов равно сумме давлений каждой компоненты смеси:

P = P₁ + P₂ + … +P_n =