Механический (классический) принцип относительности (принцип относительности Галилея)
Краткая биография Г.Галилея

Рис. 79.
ГАЛИЛЕЙ Галилео (Galilei Galileo) (15.II.1564 -–8.I.1642)— выдающийся итальянский физик и астроном, один из основателей точного естествознания, член Академии деи Линчей (1611 г.). Р. в Пизе. В 1581 г. поступил в Пизанский унивеситет, где изучал медицину. Но, увлекшись геометрией и механикой, в частности сочинениями Архимеда и Евклида, оставил университет с его схоластическими лекциями и вернулся во Флоренцию, где четыре года самостоятельно изучал математику.
С 1589 г. — профессор Пизанского ун-та, в 1592 —1610 гг. — Падуанского, в дальнейшем — придворный философ герцога Козимо II Медичи.
Оказал значительное влияние на развитие научной мысли. Именно от него берет начало физика как наука. Галилею человечество обязано двумя принципами механики, сыгравшими большую роль в развитии не только механики, но и всей физики. Это известный галилеевский принцип относительности для прямолинейного и равномерного движения и принцип постоянства ускорения силы тяжести.
Галилей установил закон инерции (1609), законы свободного падения, движения тела по наклонной плоскости (1604 — 09) и тела, брошенного под углом к горизонту, открыл закон сложения движений и закон постоянства периода колебаний маятника (явление изохронизма колебаний, 1583). От Галилея ведет свое начало динамика.
В июле 1609 г. Галилей построил свою первую подзорную трубу — оптическую систему, состоящую из выпуклой и вогнутой линз,— и начал систематические астрономические наблюдения. Это было второе рождение подзорной трубы, которая после почти 20-летней неизвестности стала мощным инструментом научного познания. Поэтому Галилея можно считать изобретателем первого телескопа. Он достаточно быстро усовершенствовал свою подзорную трубу и, как писал со временем, «построил себе прибор в такой степени чудесный, что с его помощью предметы казались почти в тысячу раз больше и более чем в тридцать раз ближе, чем при наблюдении простым глазом». В трактате «Звездный вестник», вышедшем в Венеции 12 марта 1610 г., он описал открытия, сделанные с помощью телескопа: обнаружение гор на Луне, четырех спутников у Юпитера, доказательство, что Млечный Путь состоит из множества звезд.
Астрономические открытия Галилея сыграли огромную роль в развитии научного мировоззрения, они со всей очевидностью убеждали в правильности учения Коперника, ошибочности системы Аристотеля и Птолемея, способствовали победе и утверждению гелиоцентрической системы мира. В 1632 г. вышел известный «Диалог о двух главнейших системах мира», в котором Галилей отстаивал гелиоцентрическую систему Коперника. Выход книги разъярил церковников, инквизиция обвинила Галилея в ереси и, устроив процесс, заставила публично отказаться от коперниковского учения, а на «Диалог» наложила запрет. После процесса в 1633 г. Галилей был объявлен «узником святой инквизиции» и вынужден был жить сначала в Риме, а затем в Арчертри близ Флоренции. Однако научную деятельность Галилей не прекратил, до своей болезни (в 1637 г. Галилей окончательно потерял зрение) он завершил труд «Беседы и математические доказательства, касающиеся двух новых отраслей науки», который подводил итог его физических исследований.
Изобрел термоскоп, являющийся прообразом термометра, сконструировал (1586 г.) гидростатические весы для определения удельного веса твердых тел, определил удельный вес воздуха. Выдвинул идею применения маятника в часах. Физические исследования посвящены также гидростатике, прочности материалов и т. п.
Сочинения:
1. Диалог о двух главнейших системах мира Птоломеевой и Коперниковой. М.-Л. ОГИЗ, 1948.
2. Пробирных дел мастер / Пер. Ю. А. Данилова.— М.: Наука, 1987.—272 с. — (Серия «Популярные произведения классиков естествознания»).
3. Беседы и математические доказательства, касающиеся двух новых отраслей наук (Сочинения. т.1). ГТТИ. М-Л. 1934.
4. Рассуждения о телах, плавающих в воде, и о тех, которые в ней движутся. В кТ: Архимед. Стэвин. Галилей. Паскаль. Начала гиростатики. Серия "«лассики естествознания"» ГНТТИ. М.-Л. 1933.
Механический принцип относительности
Принцип относительности – это принцип равноправия инерциальных систем отсчёта (ИСО) в классической механике, проявляющегося в том, что законы механики во всех таких системах одинаковы, был установлен Г.Галилеем в 1636 г.
Одинаковость законов механики для инерциальных систем Галилей иллюстрировал на примере явлений, происходящих под палубой корабля, покоящегося или движущегося равномерно и прямолинейно (относительно Земли, которую можно с достаточной степенью точности считать инерциальной системой отсчёта): «Заставьте теперь корабль двигаться с любой скоростью и тогда (если только движение будет равномерным и без качки в ту и другую сторону) во всех названных явлениях вы не обнаружите ни малейшего изменения и ни по одному из них не сможете установить, движется ли корабль или стоит неподвижно... Бросая какую-нибудь вещь товарищу, вы не должны будете бросать ее с большей силой, когда он будет находиться на носу, а вы на корме, чем когда ваше взаимное положение будет обратным; капли, как и ранее, будут падать в нижний сосуд, и ни одна не упадет ближе к корме, хотя, пока капля находится в воздухе, корабль пройдет много пядей» («Диалог о двух главнейших системах мира птоломеевой и коперниковой», М. — Л., 1948, с. 147).
Движение материальной точки относительно: её положение, скорость, вид траектории зависят от того, по отношению к какой системе отсчёта (телу отсчёта) это движение рассматривается. В то же время законы классической механики, т. е. соотношения, которые связывают величины, описывающие движение материальных точек и взаимодействие между ними, одинаковы во всех инерциальных системах отсчёта. Относительность механического движения и одинаковость (безотносительность) законов механики в разных инерциальных системах отсчёта и составляют содержание принципа относительности Галилея. Сам принцип логически следует из известных преобразований Галилея.
Преобразова́ния Галиле́я — в классической механике преобразования координат и скорости при переходе от одной инерциальной системы отсчета (ИСО) к другой.
Эти преобразования справедливы лишь при скоростях много меньше скорости света в вакууме ( 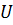 << c) и основываются на двух предположениях, которые принимались неявно и считались очевидными:
<< c) и основываются на двух предположениях, которые принимались неявно и считались очевидными:
- ход времени одинаков во всех инерциальных системах отсчета;
- линейные размеры тела не зависят от скорости его движения относительно системы отсчета.
Пусть имеются две инерциальные системы отсчёта, одну из которых, К, условимся считать покоящейся; вторая система, К′, движется по отношению к Кс постоянной скоростью 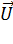 так, как показано на рис. 80.
так, как показано на рис. 80.
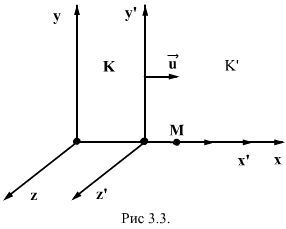
Рис. 80.
Тогда преобразования Галилея имеют вид:
x′ = x  ut,
ut,
x′ = x  ut,
ut,
y′ = y,
z′ = z,
t′ = t
или, используя векторные обозначения,
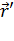 =
= 

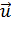 t,
t,
t′  t
t
(последняя формула остается верной для любого направления осей координат).
Из преобразований Галилея следуют:
- классический закон сложения скоростей: 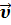 =
= 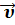 ’ +
’ + 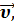
где 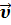 – скорость точки М в «неподвижной» системе отсчета К,
– скорость точки М в «неподвижной» системе отсчета К, 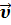 ’ – скорость точки М в движущейся системе К′;
’ – скорость точки М в движущейся системе К′;
- инвариантность (неизменность) ускорения точки М и сил, действующих на неё:
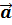 =
= 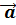 ’,
’,
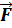 =
= 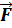 ’.
’.
Из последних соотношений следует, что уравнение второго закона Ньютона не изменяется при переходе от одной ИСО к другой, т.е. законы Ньютона инвариантны к преобразованиям Галилея.
Современные формулировки классического принципа относительности:
1). Во всех ИСО при одних и тех же условиях все механические явления протекают одинаково.
2). Законы классической механики инвариантны относительно перехода их одной ИСО в другую.
В современной физике показано, что классический принцип относительности свидетельствует о том, что все ИСО равноправны, «абсолютной» системы отсчета нет.
Принцип относительности Галилея справедлив лишь в классической механике, в которой рассматриваются движения со скоростями, много меньшими скорости света. При скоростях, близких к скорости света, движение тел подчиняется законам релятивистской механики Эйнштейна, которые инвариантны по отношению к другим преобразованиям координат и времени Лоренца.
Неинерциальные системы отсчёта
Неинерциальными системами отсчёта (НСО) называются системы отсчёта, движущиеся относительно инерциальной системы с ускорением.
Все реальные системы отсчёта неинерциальные. Законы Ньютона выполняются лишь в инерциальных системах отсчёта.
В НСО тело движется с ускорением и в тех случаях, когда на него внешние силы не действуют.
Например, если автобус движется с ускорением 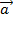 относительно Земли, то в системе отсчета, связанной с автобусом, на все тела будет действовать сила инерции Fi (см. рис.81).
относительно Земли, то в системе отсчета, связанной с автобусом, на все тела будет действовать сила инерции Fi (см. рис.81).
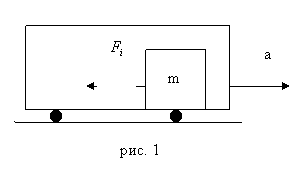
Рис. 81.
В НСО кроме сил, обусловленных взаимодействием, имеются силы, обусловленные неинерциальностью самих систем отсчёта, - так называемые силы инерции.
Если НСО движется с постоянным ускорением  то по отношению к ней все тела, покоящиеся или движущиеся прямолинейно и равномерно по отношению к ИСО, будет двигаться с ускорением (
то по отношению к ней все тела, покоящиеся или движущиеся прямолинейно и равномерно по отношению к ИСО, будет двигаться с ускорением (  . Ускорение (
. Ускорение (  создаётся силой (
создаётся силой (  ). Эта сила и есть сила инерции.
). Эта сила и есть сила инерции.
Если тело в НСО находится во взаимодействии с другими телами, то сила инерции добавится к силам, обусловленным взаимодействием. Поэтому второй закон Ньютона в НСО имеет вид:
 =
=  ,
,
где  -–результирующая сила, обусловленная взаимодействием тел;
-–результирующая сила, обусловленная взаимодействием тел;  -–сила инерции.
-–сила инерции.
Введение сил инерции даёт возможность описывать движение тел в любых системах отсчёта с помощью одних и тех же уравнений движения, т.е. второй закон Ньютона будет справедлив в любой системе отсчёта.
В зависимости от характера движения НСО выражение для сил инерции будет иметь разный вид.
Примеры сил инерции
а) центробежная сила инерции
Центробежная сила - сила, с которой движущаяся материальная точка действует на тело (связь), стесняющее свободу движения точки и вынуждающее её двигаться криволинейно. Эта сила действует всегда только в одном направлении – от центра вращения.
Для материальной точки центробежная сила выражается формулой:
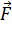 =
=  m[
m[ 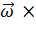 [
[ 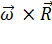 ]] = m (
]] = m ( 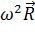
 (
( 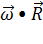 )
) 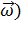 ,
,
где:
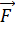 — центробежная сила приложенная к телу,
— центробежная сила приложенная к телу,
m — масса тела,
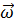 — угловая скорость вращения неинерциальной системы отсчёта относительно инерциальной (направление вектора угловой скорости определяется по правилу буравчика),
— угловая скорость вращения неинерциальной системы отсчёта относительно инерциальной (направление вектора угловой скорости определяется по правилу буравчика),
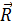 — радиус-вектор тела во вращающейся системе координат.
— радиус-вектор тела во вращающейся системе координат.
Эквивалентное выражение для центробежной силы можно записать как
 = m
= m  R0,
R0,
если использовать обозначение 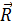 0 для вектора, перпендикулярного оси вращения и проведенного от неё к данной материальной точке.
0 для вектора, перпендикулярного оси вращения и проведенного от неё к данной материальной точке.
Центробежная сила и центростремительная сила численно равны друг другу и направлены вдоль одной прямой в противоположные стороны, но приложены к разным телам, как силы действия и противодействия. Например, при вращении в горизонтальной плоскости привязанного к верёвке груза центростремительная сила действует со стороны верёвки на груз, вынуждая его двигаться по окружности, а центробежная сила действует со стороны груза на верёвку, натягивая её (рис. 82).
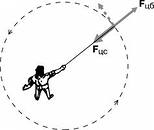
Рис. 82.
б) сила Кориолиса
Си́ла Кориоли́са — одна из сил инерции, существующая в неинерциальной системе отсчёта из-за вращения и законов инерции, проявляющаяся при движении в направлении под углом к оси вращения. Названа по имени французского учёного Гюстава Гаспара Кориолиса, впервые описавшего её в статье, опубликованной в 1835 году.
Появление кориолисовой силы можно обнаружить на следующем примере. Возьмем горизонтально расположенный диск, который может вращаться вокруг вертикальной оси. Прочертим на диске радиальную прямую ОА (рис. 83).
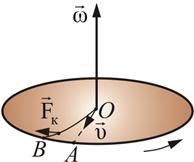
Рис. 83.
Запустим в направлении от О к А шарик со скоростью 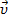 . Если диск не вращается, шарик должен катиться вдоль ОА. Если же диск привести во вращение в направлении, указанном стрелкой, то шарик будет катиться по кривой 0В, причем его скорость относительно диска быстро изменяет свое направление. Следовательно, по отношению к вращающейся системе отсчета шарик ведет себя так, как если бы на него действовала сила
. Если диск не вращается, шарик должен катиться вдоль ОА. Если же диск привести во вращение в направлении, указанном стрелкой, то шарик будет катиться по кривой 0В, причем его скорость относительно диска быстро изменяет свое направление. Следовательно, по отношению к вращающейся системе отсчета шарик ведет себя так, как если бы на него действовала сила 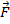 к,, перпендикулярная направлению движения шарика. Действительно, при вращении диска более далёкие от центра точки движутся с большей касательной скоростью, чем менее далёкие. Переместить некоторое тело вдоль радиуса так, чтобы оно оставалось на радиусе можно, увеличив скорость тела, т. е. придав ему ускорение.
к,, перпендикулярная направлению движения шарика. Действительно, при вращении диска более далёкие от центра точки движутся с большей касательной скоростью, чем менее далёкие. Переместить некоторое тело вдоль радиуса так, чтобы оно оставалось на радиусе можно, увеличив скорость тела, т. е. придав ему ускорение.
Причина появления силы Кориолиса — в кориолисовом (поворотном) ускорении. В инерциальных системах отсчёта действует закон инерции, то есть, каждое тело стремится двигаться по прямой и с постоянной скоростью. Если рассмотреть движение тела, равномерное вдоль некоторого вращающегося радиуса и направленное от центра, то станет ясно, что чтобы оно осуществилось, требуется придавать телу ускорение, так как чем дальше от центра, тем должна быть больше касательная скорость вращения. Это значит, что с точки зрения вращающейся системы отсчёта, некая сила будет пытаться сместить тело с радиуса. Если вращение происходит по часовой стрелке, то двигающееся от центра вращения тело будет стремиться сойти с радиуса влево. Если вращение происходит против часовой стрелки — то вправо.
Ускорение направлено перпендикулярно векторам 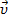 и
и 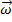 и максимально, если относительная скорость точки
и максимально, если относительная скорость точки 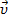 ортогональна угловой скорости
ортогональна угловой скорости 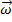 вращения подвижной системы отсчета. Кориолисово ускорение равно нулю, если угол между векторами
вращения подвижной системы отсчета. Кориолисово ускорение равно нулю, если угол между векторами 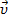 и
и 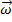 равен нулю или π, либо если хотя бы один из этих векторов равен нулю.
равен нулю или π, либо если хотя бы один из этих векторов равен нулю.
Таким образом, 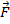 к всегда лежит в плоскости, перпендикулярной к оси вращения. Сила Кориолиса возникает только в случае, когда тело изменяет свое положение по отношению к вращающейся системе отсчета.
к всегда лежит в плоскости, перпендикулярной к оси вращения. Сила Кориолиса возникает только в случае, когда тело изменяет свое положение по отношению к вращающейся системе отсчета.
Пример.
Пусть имеются две системы отсчёта, одна из которых S инерциальная, а другая S′движется относительно первой произвольным образом и в общем случае является неинерциальной (рис. 84). Будем также рассматривать движение произвольной материальной точки массы m. Её ускорение по отношению к первой системе отсчёта обозначим  a, а по отношению ко второй —
a, а по отношению ко второй —  r.
r.
Связь между ускорениями  a и следует из теоремы Кориолиса:
a и следует из теоремы Кориолиса:  a =
a =  r +
r +  e +
e +  k,
k,
где  e — перено́сное ускорение, а
e — перено́сное ускорение, а  k— ускорение Кориолиса (кориолисово ускорение, поворотное ускорение). Напомним, что переносным ускорением называют ускорение той точки системы S′ относительно системы S, в которой в данный момент находится рассматриваемая материальная точка.
k— ускорение Кориолиса (кориолисово ускорение, поворотное ускорение). Напомним, что переносным ускорением называют ускорение той точки системы S′ относительно системы S, в которой в данный момент находится рассматриваемая материальная точка.
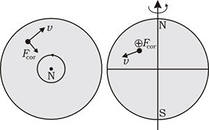
Рис. 84.
После умножения на массу точки и учёта второго закона Ньютона m 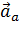 =
= 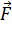 , данное соотношение можно представить в виде: m
, данное соотношение можно представить в виде: m  r =
r = 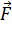 + (
+ (  m
m  e) + (
e) + (  m
m  k) • (
k) • (  m
m  k).
k).
Величину 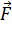 e = (
e = (  m
m  e) называют переносной силой инерции, а величину
e) называют переносной силой инерции, а величину 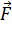 k = (
k = (  m
m  k) — силой Кориолиса (кориолисовой силой). Соответственно можно записать:
k) — силой Кориолиса (кориолисовой силой). Соответственно можно записать:
m  r =
r = 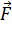 +
+ 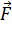 e +
e + 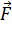 k.
k.
Полученное выражение выражает основной закон динамики для неинерциальных систем отсчёта.
Из кинематики известно, что  k = 2 [
k = 2 [ 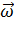
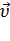 r],
r],
где 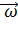 — угловая скорость вращения неинерциальной системы отсчёта S′,
— угловая скорость вращения неинерциальной системы отсчёта S′, 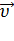 — скорость движения рассматриваемой материальной точки в этой системе отсчёта; квадратными скобками обозначена операция векторного произведения. С учётом этого для силы Кориолиса выполняется
— скорость движения рассматриваемой материальной точки в этой системе отсчёта; квадратными скобками обозначена операция векторного произведения. С учётом этого для силы Кориолиса выполняется
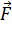 k.=
k.=  2m [
2m [ 
 r].
r].
Влияние кориолисовых сил необходимо учитывать в ряде случаев при истолковании явлений, связанных с движением тел относительно земн ой поверхности. Например, при свободном падении тел на них действует кориолисова сила, обусловливающая отклонение к востоку от линии отвеса. Эта сила максимальна на экваторе и обращается в нуль на полюсах. Летящий снаряд также испытывает отклонения, обусловленные кориолисовыми силами инерции. Например, при выстреле из орудия, направленного на север, снаряд будет отклоняться к востоку в северном полушарии и к западу – в южном. При стрельбе вдоль экватора силы Кориолиса будут прижимать снаряд к Земле, если выстрел произведен в восточном направлении.
Сила Кориолиса действует на тело, движущееся вдоль меридиана в северном полушарии вправо и в южном – влево (рис. 85).
Это приводит к тому, что у рек подмывается всегда правый берег в северном полушарии и левый – в южном. Эти же причины объясняют неодинаковый износ рельсов железнодорожных путей.
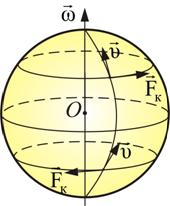
Рис. 85.
В результате воздействия этой силы движущиеся объекты, океанские и атмосферные течения отклоняются в правую сторону в северном полушарии и в левую сторону -–в южном. Это явление сильно влияет на погодные условия в масштабах всего мира. Примером действия этого эффекта является воронкообразное движение воды, выливающейся сквозь отверстие, или воздушного вихря.
Силы Кориолиса проявляются и при качаниях маятника (маятник Фуко). Для простоты предположим, что маятник расположен на полюсе. На северном полюсе сила Кориолиса будет направлена вправо по ходу маятника. В итоге траектория движения маятника будет иметь вид розетки.
| В технике сила Кориолиса учитываются в теории гироскопов, турбин и многого др. |
Следовательно, в общем случае, при использовании уравнений Ньютона во вращающейся системе отсчета, возникает необходимость учитывать центробежную, центростремительную силы инерции, а также кориолисову силу.
Вывод:одним из фундаментальныхпринципов общей теории относительности (А.Эйнштейн, 1916) является обобщённый принцип относительности:
Законы физики при одних и тех же условиях протекают одинаково в любых (инерциальных и неинерциальных) системах отсчёта.
