Понятия о погрешностях измерений
Измерить какую-либо величину – значит определить опытным путем соотношение между этой величиной и некоторым ее значением, принятым за единицу.
В зависимости от того, каким способом находят числовые значения искомой величины, измерения подразделяются на два вида – прямые и косвенные.
При прямых измерениях результат получается непосредственно с помощью средств измерений, градуированных в соответствующих единицах. К прямым измерениям относятся, например, определение температуры термометром, электрического напряжения – вольтметром.
К косвенным измерениям относятся такие, при которых значения интересующих нас величин вычисляются по результатам прямых измерений одной или нескольких других величин, связанных с искомой величиной известной зависимостью. Например, изменение внутренней энергии газа в термодинамическом процессе определяется косвенно по известным значениям теплоемкости и измеренным значениям температуры.
Даже при самом тщательном измерении какой-либо величины не представляется возможным получить результат абсолютно свободный от искажений. Причины этих искажений различны – несовершенство средств и методов измерения, непостоянство условий измерения и ряд других.
Искажениями обусловлена так называемая погрешность измерения – отклонение результата измерения от истинного значения измеряемой величины. В задачу измерения всегда входит не только нахождение самой величины, но и оценка допущенной при измерении погрешности.
Погрешности измерений по способу их числового выражения подразделяют на абсолютные, выраженные в единицах измеряемой величины, и относительные, выраженные в процентах или долях этой величины. Погрешности вычисляются по следующим формулам:
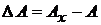 и
и 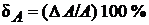 ,
,
где 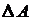 – абсолютная погрешность измерения;
– абсолютная погрешность измерения; 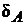 – относительная погрешность измерения,
– относительная погрешность измерения, 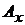 – измеренное значение величины; A – истинное ее значение.
– измеренное значение величины; A – истинное ее значение.
Строго говоря, истинное значение измеряемой величины всегда остается неизвестным. Поэтому практически под истинным значением величины понимают ее значение, найденное измерением с помощью приборов и методов более высокой точности.
Относительная погрешность дает более непосредственное, осязаемое представление о точности выполненного измерения, чем абсолютная.
Действительно, если измерить длину карандаша (10 см) с абсолютной погрешностью 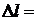 ±1 см, то такое измерение нельзя признать особенно точным и ему соответствует довольно большая относительная погрешность, равная ±10%.
±1 см, то такое измерение нельзя признать особенно точным и ему соответствует довольно большая относительная погрешность, равная ±10%.
Если с такой же абсолютной погрешностью ( 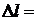 ±1 см) измерить длину помещения (10 м), то это измерение значительно более точное и характеризуется малой относительной погрешностью, равной ±0,1%.
±1 см) измерить длину помещения (10 м), то это измерение значительно более точное и характеризуется малой относительной погрешностью, равной ±0,1%.
В практике часто используют понятие “точность измерений”. Обычно точность измерений характеризуют величиной максимально возможной (так назы-
ваемой предельной) относительной погрешности. Поэтому, если утверждают, что точность измерения величины A равна ±1,5%, то это означает, что относительная погрешность измерения данной величины не превосходит ±1,5% (но фактически может быть и меньше).
Погрешности измерений по характеру их проявления подразделяют на систематические, случайные и грубые. Систематические погрешности остаются постоянными или же закономерно изменяются при повторных измерениях одной и той же величины. Случайные погрешности возникают в результате совокупного действия различных случайных причин и являются неопределенными по величине и знаку. Их влияние на результаты измерений учитывают методами математической статистики. Грубые погрешности чаще всего связаны с резким нарушением условий измерений. Результаты, содержащие грубые ошибки, должны быть отброшены как недостоверные.
| Лабораторная работа № 2 | ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ ПОЛИТРОПЫ РАСШИРЕНИЯ ВОЗДУХА |
Назначение работы. Определение показателя политропы расширения воздуха с помощью экспериментальной установки.
 Задание
Задание
1. Провести экспериментальное исследование политропного процесса на установке.
2. Определить значение показателя политропы расширения воздуха.
3. Построить графики процессов, происходящих в установке.
Основные понятия
Из уравнения политропного процесса 1-2 (рис. 2.1)
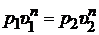 | (2.1) |
следует, что для определения величины показателя политропы достаточно знать давление и удельный объем газа в начале и конце процесса.
Логарифмируя уравнение (2.1), получим
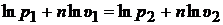 , , |
откуда
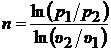 . . | (2.2) |
Экспериментальное определение показателя политропы на основе этой формулы затруднительно, так как измерить удельный объем воздуха 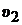 достаточно сложно. Поэтому формулу (2.2) целесообразно представить в другом виде так, чтобы приходилось измерять только давление. Возможность такого преобразования легко установить, рассмотрев рис. 2.1, на котором кроме политропного процесса расширения 1-2 изображен изохорный процесс 2-3 нагревания воздуха до температуры
достаточно сложно. Поэтому формулу (2.2) целесообразно представить в другом виде так, чтобы приходилось измерять только давление. Возможность такого преобразования легко установить, рассмотрев рис. 2.1, на котором кроме политропного процесса расширения 1-2 изображен изохорный процесс 2-3 нагревания воздуха до температуры 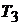 , равной
, равной 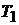 .
.
Для изотермы 1-3
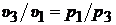 .
.
Но 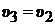 , поэтому
, поэтому
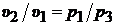 .
.
С учетом последнего соотношения формулу (2.2) можно записать в виде
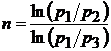 . . | (2.3) |
Формула (2.3) является расчетной. Из нее следует, что для определения показателя политропы необходимо измерить давление в начале и конце политропного расширения ( 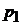 и
и 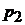 ) и давление (
) и давление ( 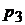 ) в конце последующего изохорного нагревания воздуха до температуры окружающей среды
) в конце последующего изохорного нагревания воздуха до температуры окружающей среды 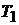 )
)
Экспериментальная установка
Принципиальная схема экспериментальной установки показана на рис. 2.2. В состав установки входит металлический бак 3 вместимостью 40 л, оснащенный краном 4 для выпуска воздуха, U-образный жидкостный манометр 2 для
измерения избыточного давления в баке, ручной насос 1 для нагнетания воздуха.
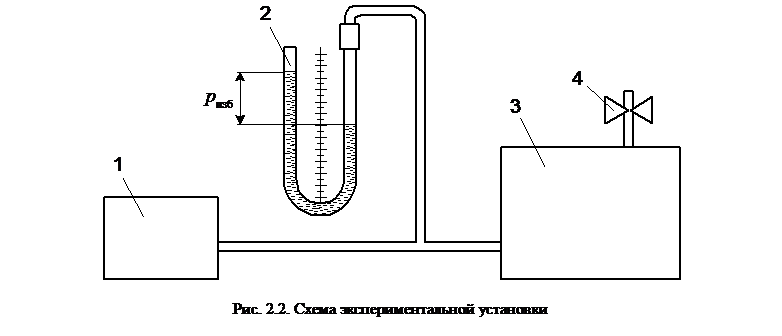
Параметры состояния атмосферного воздуха в лаборатории во время проведения опыта регистрируются термометром и барометром.
Порядок выполнения работы
1. Записать параметры состояния атмосферного воздуха – температуру 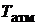 и давление
и давление 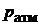 – в протокол наблюдений.
– в протокол наблюдений.
Протокол наблюдений
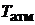 , К , К | 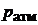 , Па , Па | 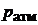 , мм вод. ст. , мм вод. ст. |  , мм вод. ст. , мм вод. ст. | 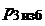 , мм вод. ст. , мм вод. ст. |
2. С помощью насоса произвести нагнетание воздуха в бак до избыточного давления 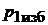 , величина которого ограничивается высотой трубок манометра. В результате температура воздуха в баке несколько возрастет.
, величина которого ограничивается высотой трубок манометра. В результате температура воздуха в баке несколько возрастет.
3. Выждать 5-7 минут, в течение которых воздух в баке охладится до температуры 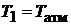 . О достижении этой температуры можно судить по установившемуся показанию жидкостного манометра. Величину избыточного давления
. О достижении этой температуры можно судить по установившемуся показанию жидкостного манометра. Величину избыточного давления  в миллиметрах водяного столба записать в протокол наблюдений.
в миллиметрах водяного столба записать в протокол наблюдений.
4.
5. Резко открыть кран и следить за показаниями манометра. При достижении равенства уровней воды в трубках манометра, т. е. после расширения воздуха в баке до давления 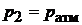 , кран закрыть и снова следить за показаниями манометра.
, кран закрыть и снова следить за показаниями манометра.
В результате расширения воздуха температура в баке уменьшится до 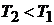 . Поэтому после закрытия крана воздух станет нагреваться вследствие теплообмена с окружающей средой через стенки бака. Процесс нагревания воздуха происходит по изохоре 2 – 3 с возрастанием давления до
. Поэтому после закрытия крана воздух станет нагреваться вследствие теплообмена с окружающей средой через стенки бака. Процесс нагревания воздуха происходит по изохоре 2 – 3 с возрастанием давления до  (см. рис. 2.1).
(см. рис. 2.1).
6. После полного прекращения роста давления в баке измерить и записать в протокол наблюдений избыточное давление 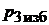 в конце изохорного процесса.
в конце изохорного процесса.
