Измерение ионной проводимости

Твёрдых электролитов

В основе метода лежит представление электрохимической ячейки с двумя одинаковыми электродами Ме/электролит/Ме в виде эквивалентной цепи переменного тока, содержащей электродный импеданс Z и объемное сопротивление электролита R_э.

В свою очередь электродный импеданс удобно представить как последовательное соединение ёмкости С_s и активного сопротивления R_s, что аналитически выражается уравнением

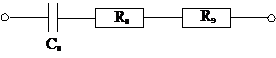Z = R_s + (iwC_s)^-1, (1.20)

где i= 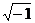, w – круговая частота переменного тока.

Так как R_s и R_э включены последовательно, то любые измерения при фиксированной частоте могут дать лишь активную составляющую полного импеданса ячейки, равную сумме

R_изм = R_s + R_э. (1.21)

Сопротивление R_s в общем случае зависит от частоты, величины поверхности контакта электрод-электролит, состояния этой поверхности и т.п. Поэтому (1.21) можно переписать в виде

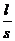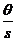R_изм=ρ +2 , (1.22)

где ρ – удельное сопротивление электролита; θ – эффективное сопротивление единицы видимой поверхности контакта электрод-электролит; 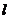, s - толщина электролита и его поперечное сечения соответственно.

Величина θ практически всегда уменьшается с ростом частоты. Поэтому при достаточно больших частотах переменного тока вторым членом уравнения можно пренебречь и считать, что:

R_изм = ρ 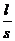= R_э (1.23)

Признаком применимости соотношения (1.23) является независимость измеренного сопротивления от частоты. Однако случаи с частотно независимыми областями встречаются не для всех соединений. При наличии хорошо воспроизводимых контактов металл-электролит можно вести измерения, постепенно уменьшая толщину электролита (или используя несколько образцов разной толщины). При этом:

SR_изм = 2θ + ρ 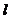, (1.24)

т.е. график SR_изм от 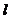должен иметь вид прямой с наклоном, равным ρ. Другой более распространённый путь – проведение измерений в широком диапазоне частот и экстраполяция результатов на бесконечную частоту. Решение этой задачи осложняется тем, что θ не является линейной функцией частоты.

На практике, однако, даже при выполнении этого требования не всегда удается достичь желаемой точности. В этом случае действительная величина объемного сопротивления может быть определена лишь путём анализа импеданса с использованием графоаналитического метода.

Формулу (1.19) можно представить в виде:

σ_k = 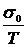exp(-U/kT), (1.25)

где σ₀ - константа. Умножим обе части уравнения на Т и прологарифмируем

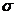ln T=ln 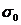- 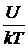, (1.26)

По углу наклона прямой к оси абсцисс tgα = 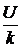можно определить энергию активации.

Для определения температуры перехода AgI в суперионное состояние, определения энергии активации проводимости до и после суперионного перехода необходимо получить зависимость проводимости от температуры.

Установка для измерения ионной проводимости состоит из ячейки с образцом, нагревателя, блока питания нагревателя, измерительного прибора (мост переменного тока или импедансметра).

Образец представляет собой таблетку AgI (d=8 мм, h=2 мм), спрессованную вместе с электродами из мелкодисперсного серебра под давлением 10⁸ Па.

1.3. Задание на работу.

1. Ознакомиться с правилами работы на измерительном приборе (описание к мосту Р 51021).

2. Получить при комнатной температуре зависимость проводимости образца от частоты в интервале 200¸200000 Гц.

3.Получить зависимость проводимости образца от Т в интервале 30¸180 ⁰С с шагом в 10 ⁰С при нагреве.

4. Рассчитать удельную электропроводность образца и построить график

Ln = .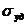

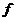
5. Определить Т_о перехода в суперионное состояние, энергию активации ионной проводимости при Т выше и ниже Т_с фазового перехода.

6. Сделать выводы.

1.4. Вопросы для контроля.

1. Какие частицы являются носителями заряда в твёрдом теле?

2.Каково необходимое условие подвижности ионов в твёрдом теле?

3. Назовите основные классы твёрдых электролитов.

4. Как влияют состав и структура твёрдого тела на подвижность ионов?

5. Какими величинами характеризуются транспортные свойства твёрдых электролитов?

6.Какой физический смысл имеет энергия активации проводимости?

7. Как влияет температура на ионную проводимость ?

8. Каким образом можно определить энергию активации проводимости?

Литература

1. Укше Е. А. Твердые электролиты. М.: Наука, 1977, 175 с.

2. Чеботин В.Н., Перфильев М.В. Электрохимия твердых электролитов. М.: Химия, 1978, 312 с.

1.Павлов П.В., Хохлов А.Ф. Физика твердого тела. М: Высшая школа. 2000 г. с. 447.

2.Орешкин П.Т. Физика полупроводников и диэлектриков. М: Высшая школа 1977 г.

2.Борисова М.Э., Койков С.Н. Физика диэлектриков. М: Высшая школа. 1979г.

.

5.Вилков Л.В., Пентин Ю.А. Физические методы исследования в химии. Структурные методы и оптическая спектроскопия: Учеб. М.: Высш. шк., 1987. 366 с.

3.Бурмистров В.А., Полевой Б.Г. Лабораторный практикум: «Твердые электролиты. Поляризация диэлектриков в переменном поле» Метод. разработка., Из-во. ЧелГУ, 1994г., с.32.