Проводимость ионных кристаллов

ТВЕРДЫЕ ЭЛЕКТРОЛИТЫ

Цель работы: Ознакомиться с теоретическими основами ионного транспорта твердых электролитов, освоить метод измерения ионной электропроводности материалов от температуры; определить энергию активации и величину электропроводности, температуру перехода твердого электролита в суперионное состояние.

Измерение ионной проводимости

Твёрдых электролитов

В основе метода лежит представление электрохимической ячейки с двумя одинаковыми электродами Ме/электролит/Ме в виде эквивалентной цепи переменного тока, содержащей электродный импеданс Z и объемное сопротивление электролита R_э.

В свою очередь электродный импеданс удобно представить как последовательное соединение ёмкости С_s и активного сопротивления R_s, что аналитически выражается уравнением

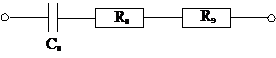Z = R_s + (iwC_s)^-1, (1.20)

где i= 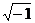, w – круговая частота переменного тока.

Так как R_s и R_э включены последовательно, то любые измерения при фиксированной частоте могут дать лишь активную составляющую полного импеданса ячейки, равную сумме

R_изм = R_s + R_э. (1.21)

Сопротивление R_s в общем случае зависит от частоты, величины поверхности контакта электрод-электролит, состояния этой поверхности и т.п. Поэтому (1.21) можно переписать в виде

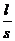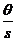R_изм=ρ +2 , (1.22)

где ρ – удельное сопротивление электролита; θ – эффективное сопротивление единицы видимой поверхности контакта электрод-электролит; 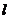, s - толщина электролита и его поперечное сечения соответственно.

Величина θ практически всегда уменьшается с ростом частоты. Поэтому при достаточно больших частотах переменного тока вторым членом уравнения можно пренебречь и считать, что:

R_изм = ρ 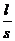= R_э (1.23)

Признаком применимости соотношения (1.23) является независимость измеренного сопротивления от частоты. Однако случаи с частотно независимыми областями встречаются не для всех соединений. При наличии хорошо воспроизводимых контактов металл-электролит можно вести измерения, постепенно уменьшая толщину электролита (или используя несколько образцов разной толщины). При этом:

SR_изм = 2θ + ρ 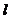, (1.24)

т.е. график SR_изм от 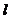должен иметь вид прямой с наклоном, равным ρ. Другой более распространённый путь – проведение измерений в широком диапазоне частот и экстраполяция результатов на бесконечную частоту. Решение этой задачи осложняется тем, что θ не является линейной функцией частоты.

На практике, однако, даже при выполнении этого требования не всегда удается достичь желаемой точности. В этом случае действительная величина объемного сопротивления может быть определена лишь путём анализа импеданса с использованием графоаналитического метода.

Формулу (1.19) можно представить в виде:

σ_k = 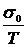exp(-U/kT), (1.25)

где σ₀ - константа. Умножим обе части уравнения на Т и прологарифмируем

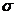ln T=ln 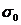- 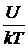, (1.26)

По углу наклона прямой к оси абсцисс tgα = 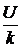можно определить энергию активации.

Для определения температуры перехода AgI в суперионное состояние, определения энергии активации проводимости до и после суперионного перехода необходимо получить зависимость проводимости от температуры.

Установка для измерения ионной проводимости состоит из ячейки с образцом, нагревателя, блока питания нагревателя, измерительного прибора (мост переменного тока или импедансметра).

Образец представляет собой таблетку AgI (d=8 мм, h=2 мм), спрессованную вместе с электродами из мелкодисперсного серебра под давлением 10⁸ Па.

1.3. Задание на работу.

1. Ознакомиться с правилами работы на измерительном приборе (описание к мосту Р 51021).

2. Получить при комнатной температуре зависимость проводимости образца от частоты в интервале 200¸200000 Гц.

3.Получить зависимость проводимости образца от Т в интервале 30¸180 ⁰С с шагом в 10 ⁰С при нагреве.

4. Рассчитать удельную электропроводность образца и построить график

Ln = .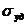

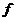
5. Определить Т_о перехода в суперионное состояние, энергию активации ионной проводимости при Т выше и ниже Т_с фазового перехода.

6. Сделать выводы.

1.4. Вопросы для контроля.

1. Какие частицы являются носителями заряда в твёрдом теле?

2.Каково необходимое условие подвижности ионов в твёрдом теле?

3. Назовите основные классы твёрдых электролитов.

4. Как влияют состав и структура твёрдого тела на подвижность ионов?

5. Какими величинами характеризуются транспортные свойства твёрдых электролитов?

6.Какой физический смысл имеет энергия активации проводимости?

7. Как влияет температура на ионную проводимость ?

8. Каким образом можно определить энергию активации проводимости?

Литература

1. Укше Е. А. Твердые электролиты. М.: Наука, 1977, 175 с.

2. Чеботин В.Н., Перфильев М.В. Электрохимия твердых электролитов. М.: Химия, 1978, 312 с.

1.Павлов П.В., Хохлов А.Ф. Физика твердого тела. М: Высшая школа. 2000 г. с. 447.

2.Орешкин П.Т. Физика полупроводников и диэлектриков. М: Высшая школа 1977 г.

2.Борисова М.Э., Койков С.Н. Физика диэлектриков. М: Высшая школа. 1979г.

.

5.Вилков Л.В., Пентин Ю.А. Физические методы исследования в химии. Структурные методы и оптическая спектроскопия: Учеб. М.: Высш. шк., 1987. 366 с.

3.Бурмистров В.А., Полевой Б.Г. Лабораторный практикум: «Твердые электролиты. Поляризация диэлектриков в переменном поле» Метод. разработка., Из-во. ЧелГУ, 1994г., с.32.

ЭЛЕКТРИЧЕСКОМ ПОЛЕ

Цель работы:Ознакомиться с основами теории поляризации диэлектриков. Овладеть умениями и навыками измерения основных параметров диэлектриков.

Релаксационная поляризация

Релаксационная поляризация диэлектрика есть процесс постепенного изменения с течением времени, приводящий к достижению равновесного значения поляризации при заданном значении напряженности 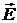электрического поля.

Релаксационные процессы в диэлектрике описываются на основе трех уравнений, установленных полуэмпирически (5), (6), (7). Основной характеристикой релаксационных процессов является время релаксации t, характеризующее среднее время перехода частицы в диэлектрике между двумя эквивалентными энергетическими состояниями, разделенными потенциальным барьером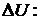

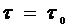
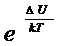. (2.5)

В простейшем случае релаксационные процессы описываются функцией последействия

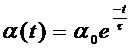, (2.6)

и функцией спадания

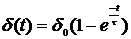, (2.7)

Если диэлектрик, имеющий релаксационную природу поляризации, поместить в электрическое поле, которое практически мгновенно изменяет свое значение от 0 до 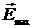, то поляризация диэлектрика будет изменяться от 0 до значения P_s (при t 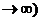c запаздыванием в два этапа:

1.Установление быстрых процессов поляризации (электронно- и ионно-деформационной).

2.Установление медленных процессов поляризации – релаксационные виды поляризации.

Установлению быстрых процессов поляризации соответствует оптическая диэлектрическая проницаемость

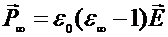. (2.8)

Установившемуся значению поляризации P_s - статическая диэлектрическая проницаемость :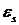

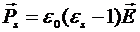. (2.9)

Из (2.8) и (2.9) следует, что релаксационная часть поляризации 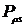может быть вычислена следующим образом:

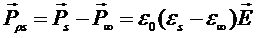. (2.10)

Согласно (2.6) и (2.7) зависимость поляризации от времени при наличии одного времени релаксации (t):

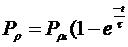) - в момент включения поля (2.11)

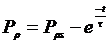- в момент отключения поля (2.12)

Если диэлектрик поместить в синусоидальное поляризующее поле:

E(t)=E_msinwt , (2.13)

где w - частота, t – время, E_m – амплитуда, то поляризация будет меняться более сложным образом:

E(t)= 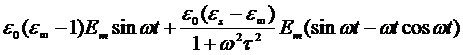. (2.14)

В уравнении (2.14) присутствует слагаемое, содержащее косинус, из чего следует, что происходит отставание поляризации по фазе от поляризующего электрического поля. Это является следствием рассеяния энергии в диэлектрике - диэлектрических потерь.

Одним из важнейших параметров, характеризующих диэлектрические потери, является тангенс угла диэлектрических потерь tgd.

Если рассмотреть векторную диаграмму токов для конденсатора с потерями, то tgd определяется отношением амплитуд активного и реактивной компонент тока:

tgd= 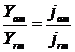, (2.15)

что позволяет связать tgd с электропроводностью диэлектрика:

tgd= = ;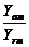

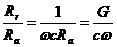G=wctgd, (2.16)

где w - частота электрического поля [Гц]; С – емкость конденсатора [Ф]; G – проводимость [См/м].

Поведение диэлектрика в переменном синусоидальном поле описывается уравнением Дебая. Уравнения Дебая получаются из приведенных выше соотношений.

Полная плотность тока, протекающего через диэлектрик, складывается из тока сквозной проводимости j_ск и тока смещения j_см:

j= j_cn+ j_cn=j_amsinwt+j_rmcoswt=j_a+ij_r . (2.17)

Ток сквозной проводимости обусловлен движением зарядов от одного электрода до другого согласно закону Ома:

j_ск=G_cкЕ= G_cкЕ_msinwt. (2.18)

Ток смещения обусловлен потерями в диэлектрике за счет релаксационных явлений. Из (2.13) следует:

j_cм= 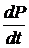(2.19)

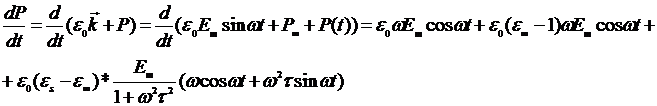
Сгруппировав члены, содержащие синусы и косинусы, получим выражение для амплитуд активных и реактивных токов:

j_am=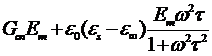

j_rm= 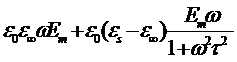. (2.20)

Подставим (2.20) в (2.15) и получим формулу, характеризующую зависимость tgd от частоты электрического поля и температуры:

tgd= 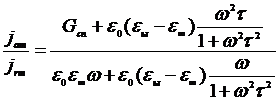. (2.21)

Если сквозная проводимость мала, то tgd обусловлен, в основном, релаксационными потерями:

tgd= 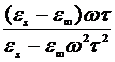. (2.22)

Типичная зависимость tgd от температуры представляет собой, согласно (2.22), сложную кривую с максимумом при

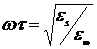. (2.23)

Одной из физических величин, характеризующих потери в диэлектрике, является комплексная часть диэлектрической проницаемости. Общий ток в диэлектрике мможно представить как изменение заряда обкладок конденсатора:

j=j_am+ij_rm=dQ/dt (2.24)

Q= 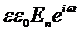(2.25)

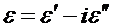(2.26)

Таким образом, диэлектрическая проницаемость представляет собой комплексную величину. Действительная часть диэлектрической проницаемости 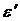обусловлена процессами поляризации, а комплексная часть 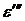- потерями энергии электрического поля на релаксационные явления и проводимость.

Из (2.24) и (2.25) с учетом (2.26) получим

j=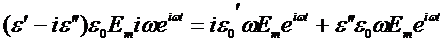

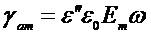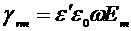, (2.27)

Приравняв амплитуды токов из (2.20) и (2.27), получим формулы Дебая:

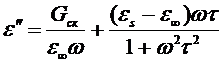
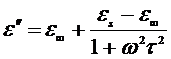(2.28)

Поскольку tgd= 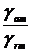, из (2.28) можно получить:

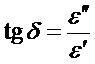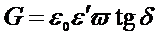, (2.29)

Как видно из (2.28) зависимостью e² от температуры является кривая с максимумом при значении

wt=1. (2.30)

По величине времени релаксации и энергии активации можно судить о природе релаксационных центров.

Существует несколько видов поляризации, протекающих в достаточно широком интервале времени. Они характеризуются различной величиной времени релаксации t и tgd. К наиболее быстрым процессам релаксационной поляризации, протекающим в интервале времени 10^-1>t>10^-7cек, относится дипольно-релаксационная поляризация и ионно-релаксационная поляризация, а к более медленным – миграционная поляризация.

.Дипольно-релаксационная поляризация. В структуре некоторых диэлектриков располагаются молекулы, обладающие дипольными моментами. Такими молекулами могут быть OH^- - группы, молекулы H₂O, CH и т.п. Без приложения к диэлектрику внешнего поля молекулы в твердом теле ориентированы хаотически и не создают эффект поляризации. При включении поля за счет время t они переориентируются по полю, занимая энергетически выгодные положения, создавая поляризованное состояние диэлектрика. Время их переориентации характеризует их взаимодействие с ближайшим окружением, а величина tgd - долю потерь (рассеяния) этими молекулами энергии электрического поля в веществе. Как правило, такие процессы, характеризуются временами релаксации, лежащими в диапазоне времени 10^-1сек>t>10^-7cек, и величиной потерь 0,001 .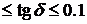

Ионно-релаксационная поляризация. Ионно-релаксационная поляризация возникает вследствие преимущественного перескока ионов по направлению поля. Рассмотрим ион, который в отсутствии поля может находиться в кристалле в двух положениях равновесия с одинаковыми минимумами потенциальной энергии. Поскольку без поля нет преимущественных направлений движения ионов, то ионы по кристаллу располагаются равномерно и поляризация диэлектрика отсутствует.

При включении электрического поля переходы иона между этими позициями становятся неравновероятными, так как энергия для перехода в одном направлении оказывается меньше на величину 1/2qEa:

E₁₂= W - 1/2qEa, (2.31)

а при переходе в противоположном направлении –на ту же величину больше

E₂₁ = W + 1/2qEa, (2.32)

где q - заряд, а – параметр. Это приводит к образованию дипольных моментов, направленных по полю, а следовательно, и поляризации диэлектрика. Такие процессы характеризуются временами релаксации 10^-1>t>10^-6 сек и потерями 0,02<tgd<1.0

Миграционная поляризация. Если ионы в кристаллах могут смещаться на достаточно большие расстояния, соизмеряемые с длиной образца, то это может приводить к образованию двойного электрического слоя вблизи электродов, что и создает дополнительную емкость при включении электрического поля.

Поскольку длина образца достаточно большая, а скорость дрейфа ионов мала, то и величина t оказывается большой. Такие процессы характеризуются большими потерями энергии.

Таким образом, по величине tgd и времени релаксации можно определить природу релаксационных процессов, участвовавших в поляризации диэлектрика.

2.2. Описание установки

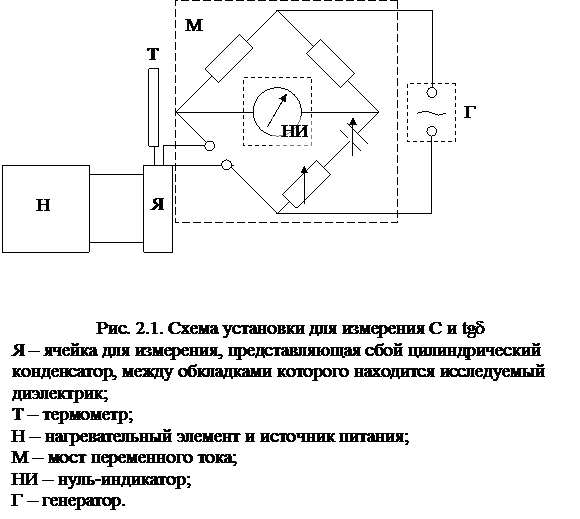В качестве объекта исследования выбрана канифоль. Установка для измерения 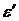и tgd представляет собой комплекс приборов и приспособлений, позволяющих проводить измерения С и tgd в диапазоне температур 22-120⁰С на частотах 0,8-10 кГц. Действительная часть диэлектрической проницаемости вычисляется по формуле 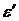=С/С₀, где С₀=8.2·10^-12Ф=8,2пФ для данной установки.

Тангенс угла потерь измеряется непосредственно мостом Р-571М. Нагрев образца до заданной температуры производится при помощи нагревательного элемента и источника питания.

Порядок выполнения работы

1.Включите мост переменного тока и дайте ему прогреться в течение 25 минут.

2.Произведите измерения С и tgd путем уравновешивания моста вращением рукояток переключателей верхнего и нижнего рядов и постепенно, увеличивая чувствительность нуль-индикатора до 30 В.

3.Произведите отсчет показаний емкости на шкалах переключателей верхнего ряда и tgd на шкале нижнего ряда и занесите в таблицу.

4.Включите блок питания нагревательного элемента и установите напряжение на нагревательном элементе последовательно: до 70⁰С – 20В, а выше 25В.

5.Проведите измерения С и tgd в интервале температур 20-140⁰С с шагом 5⁰С. Оцените ошибку измерений.

6.Постройте графики зависимости 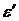, tgd и 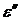от температуры. По графику 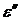=f(T) определите величину t и Т_max, а по графику tgd=f(T) время релаксации при характеристической температуре. Определить максимальную величину tgd.

7.Определите, какова природа процессов релаксации в данном диэлектрике. Сделайте выводы по работе.

Вопросы для контроля

1.Какие виды поляризации известны в диэлектриках и, какова их природа?

2.Какими соотношениями описывается поведение диэлектрика с релаксационной поляризацией в переменном электрическом поле?

3.Какие известны методы измерения 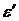, tgd от температуры и частоты?

Литература

1.Борисова М.Э., Койков С.Н. Физика диэлектриков. М: Высшая школа. 1979г.

2.Свирский М.С. Электронная теория вещества. М., 1981.

3.Ф.Эмс.Диэлектрические измерения. М.:Химия, 1967.

4.Хиппель А.Р. Диэлектрики и их применение. Из-во ГЭИ. Ленинград. 1959г.

5.Орешкин П.Т. Физика полупроводников и диэлектриков. М: Высшая школа 1977 г.

3.Бурмистров В.А., Полевой Б.Г. Лабораторный практикум: «Поляризация диэлектриков в переменном поле» Метод. разработка. Из-во. ЧелГУ, 1994г., с.32.

3. ОПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИИ ПАРАМАГНИТНЫХ ЦЕНТРОВ В КРИСТАЛЛАХ МЕТОДОМ ЭПР - СПЕКТРОСКОПИИ

Цель работы:Ознакомиться с физическими принципами метода ЭПР – спектроскопии. Выработать навыки работы на ЭПР – спектрометре.

3.1.Физические основы метода ЭПР

3.1.1. Элементарный магнитный резонанс.

Эффект магнитного резонанса состоит в том, что частица, обладающая магнитным моментом 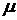, помещенная в магнитное поле 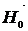, при взаимодействии с переменным магнитным полем резонансной частоты меняет свою ориентацию.

Пусть частица, обладающая магнитным моментом 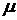, помещена в магнитное поле 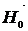. Тогда момент 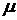будет прецессировать вокруг 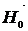с ларморовой частотой 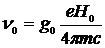, где 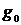- множитель Ланде. Предположим, что перпендикулярно к 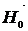наложено вращающееся с частотой 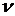слабое магнитное поле 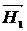. Если 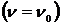частоты вращения совпадут, то под действием поля 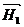, возникнет дополнительный вращательный момент, который направлен всегда так, что заставляет переориентироваться магнитный момент частицы в другую плоскость. Эффект резонанса будет тем больше, чем меньше отношение Н₁/Н₀.

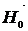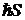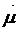Рассмотрим квантовую картину элементарного магнитного резонанса. Пусть частица обладает механическим и магнитным моментами, максимальные компоненты которых по направлению внешнего магнитного поля с напряженностью обозначим и соответственно. Как известно, 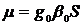(где 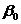- магнетон Бора) и, следовательно, в магнитном поле 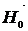возникнут 2S+1 эквивалентных уровней энергии, а именно:

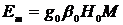, (3.1)

где М – магнитное квантовое число (S³M-S). Под действием переменного магнитного поля 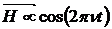возможны магнитные дипольные переходы между соседними уровнями энергии (DМ=±1), если это поле перпендикулярно к 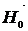и если выполнено резонансное условие:

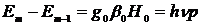. (3.2)

Когда имеется лишь два уровня энергии (S=1/2), возможны только переходы .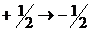

Электронный парамагнитный резонанс представляет собой явление поглощения излучения СВЧ - диапазона молекулами, ионами или атомами, обладающими электронами с не спаренными спинами. В ЭПР различные энергетические состояния обусловлены взаимодействием спинового момента не спаренного электрона 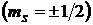с магнитным полем – так называемый электронный эффект Зеемана. Зеемановский гамильтониан, описывающий взаимодействие электрона с магнитным полем, определяется выражением 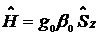, где 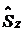- оператор спина, g - g – фактор.

Соответствующие уровни энергии будут определяться выражением (3.1) с 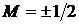, а энергия перехода формулой (3.2).

Для свободной частицы g – фактор может отклоняться от g = 2 благодаря внутренним взаимодействиям. Резонансное значение поля можно найти по формуле: ,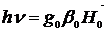

где 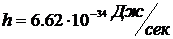- постоянная Планка; 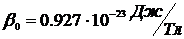- магнетон Бора; 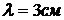- «частота» клистрона спектрометра; 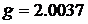- g-фактор ДФПГ.

3.1.2. Измерение интенсивности линии поглощения.

Интенсивность спектральной линии характеризуется количеством парамагнитных частиц N в объеме образца V. Для определения их концентрации используют метод сравнения с эталоном.

На практике для увеличения чувствительности спектрометра применяется модуляция магнитного поля, узкополосное усиление и фазочувствительное детектирование. На выходе фазового детектора создается напряжение U ф. д., являющееся функцией напряженности постоянного магнитного поля. В том случае, когда амплитуда модуляции 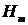значительно меньше ширины линии поглощения и усиление ведется на частоте модуляции, U д. д. пропорционально первой производной от линии поглощения.

Площадь под кривой поглощения, в таком случае, находится двойным интегрированием:

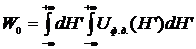. (3.3)

Произведение 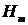на площадь под кривой поглощения пропорционально первому моменту от регистрируемой на выходе фазового детектора кривой, т. е.

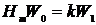, где 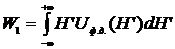. (3.4)

На пропорциональность не влияют характеристики усилителя в детекторе. С учетом этих замечаний

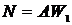, (3.5)

где А – коэффициент пропорциональности, учитывающий многие параметры (заполнение резонатора, чувствительность принимаемого тракта, усиление и т.д.). В соответствии с (3.5) считается, что количество парамагнитных частиц в образце пропорционально площади под кривой поглощения или первому моменту производной линии поглощения.

Если имеется эталонный образец, в котором число парамагнитных частиц определено независимым от ЭПР методом, то в исследуемом образце концентрацию парамагнитных центров можно вычислить по формуле

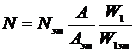. (3.6)

Если удается выполнить условие 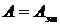, а это делается возможным, когда эталонный и исследуемый образцы дают сигнал с одинаковым g–фактором, эффективный спин S для них одинаков, а также одинаковы условия регистрации спектров в заполнение резонатора, тогда

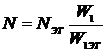. (3.7)

Если 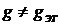, то

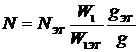. (3.8)

(g–фактор образца и эталона можно определить непосредственно из измерений).

Для определения площади под кривой производной линии поглощения используют метод численного интегрирования. Полученный экспериментально спектр разбивают на равные интервалы 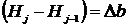(рис.3.1). Площадь спектра определяется по формуле:

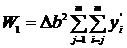, (3.9)

где 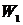-площадь под кривой поглощения, полученная численным интегрированием, соответствующая первым моментам в (3.7) и (3.8); 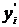- производная интенсивность сигнала ЭПР.

3.2. Устройство и порядок работы на ЭПР – спектрометре.

Для изучения спектров ЭПР в данной лабораторной работе используется спектрометр «Минск-12М». Магнитное поле создается электромагнитом. Величина поля в зазоре определяется по градуировочному графику (рис.3.2).Источником СВЧ – излучения служит клистрон. Излучение от клистрона подается по волноводу в полость резонатора, на образце концентрируется осциллирующее магнитное поле. Регулировку поступающей в резонатор мощности осуществляет аттенюатор (ослабитель). Определенная часть мощности из резонатора выводится и подается на детектор. Если внутри резонатора происходит поглощение, то ток детектора соответственно уменьшается (рис.3.3).

При высокочастотной модуляции и медленной его протяжке через резонансное значение, для какого – либо вещества происходит амплитудная модуляция СВЧ – мощности. Амплитудно-модулированный сигнал после детектирования усилителем промежуточной частоты подается на синхронный детектор. Высокочастотная модуляция магнитного поля осуществляется модуляционными катушками, на которые подается переменное напряжение высокой частоты от высокочастотного генератора. С этого же генератора подается так называемое опорное напряжение на синхронный детектор. При малой амплитуде модуляции магнитного поля (меньше ширины линии поглощения) и использовании синхронного детектирования записывают на самопишущий потенциометр производную сигнала поглощения. Поскольку частота клистрона фиксирована 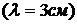, для записи спектра поглощения пользуются изменением магнитного поля, а не частоты.

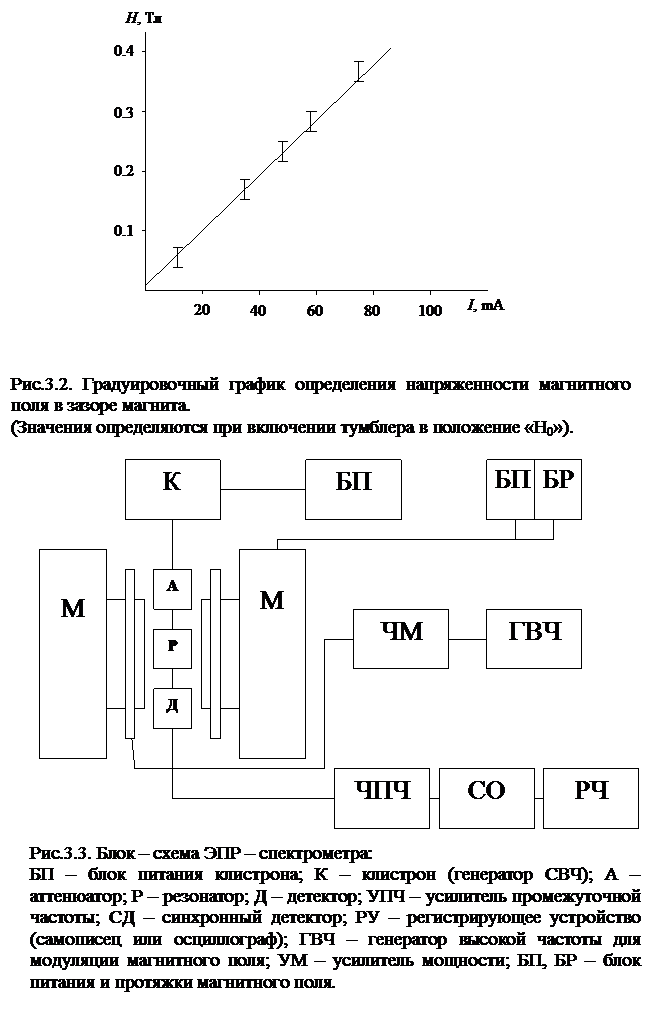
Органы управления спектрометром выведены на переднюю панель (рис.3.4).

Для записи спектра необходимо выполнить следующие операции:

- Перед включением спектрометра в сеть необходимо:

-
Установить переключатель измерительного прибора в положение «Х»;

- Ручку «модуляция» вывести в крайнее левое положение;

- Тумблер, «пуск - стоп» установить в положение «стоп».

- Тумблером «сеть» включить спектрометр. При этом должен загореться индикатор включения сети, стрелка измерительного прибора должна отклониться на половину шкалы.

- Установить переключатель измерительного прибора в положение «1 дел».

- Кратковременным нажатием кнопки запуска на верхней крышке блока СВЧ – магнита получить отклонение стрелки прибора в пределах 15-20 делений шкалы. При необходимости допускается повторить нажатие 2-3 раза.

- С помощью цангового зажима на верхней крышке блока СВЧ – магнита закрепить ампулу с образцом так, чтобы образец был расположен в центре измерительного резонатора.

- - Осуществить поиск сигнала ЭПР, используя для этого расчетные данные резонансного поля и градуировочный график (рис.3.3). Поиск сигнала осуществить следующим образом:

- Регулятор величины развертки поля «Диапазон DН» выставить в среднее положение;

- Ручки «Модуляция» и «Усиление» установить в крайние правые положения;

- Тумблеры «Пост. Времени» - в положение 0.001 и 0.1;

- Тумблеры режима – в положения «МС» и «Пуск»;

- Установить переключатель измерительного прибора в положение «Н₀»;

- Медленным вращением регуляторов напряженности магнитного поля «*1000» и «*100» выставить резонансное значение «Н₀» и вблизи его произвести поиск сигнала ЭПР. Вывести сигнал ЭПР на середину экрана осциллографа.

- Оптимизировать сигнал ЭПР на экране по минимальным искажениям выбором: уровня модуляции и величины усиления (ручки «Модуляция» и «Усиление»), диапазона DН. Осуществить совмещение сигналов прямой и обратной разверткой «Совмещение»

- После оптимизации сигнала произвести его запись на самописец. Для этого:

Включить тумблер «Сеть», «Двигатель», «Диаграмма» на самописце, поднять перо;

- Тумблеры режима спектрометра перевести в положение «С» «Стоп». Органами управления самописца вывести перо на середину осей «Х» и «У»;

- Произвести оптимизацию сигнала на самописце, имитируя запись (движение пера начинается при переводе тумблера в положение «Пуск»). Произвести выбор скорости развертки (ручка «Время развертки»), добиться максимального усиления сигнала;

- Произвести запись сигнала.

Отключение спектрометра производится в обратной последовательности.

3.3. Задание к работе

1. Ознакомиться с описанием лабораторной работы и ходом ее выполнения.

Получить спектр эталонного образца ДФПГ (дифенилпикрилгидравил, g – фактор 2.0036, DН = 2.7 Гс, N = 6.7×10²¹ 1/см³) и произвести его запись на самописце.

2. В тех же режимах записать спектр исследуемого образца (каменноугольного пека). Определить концентрацию парамагнитных центров в исследуемом образце и g – фактор.

3. Ответить на предложенные вопросы и оформить отчет по работе.

3.4. Вопросы для контроля

1. Каковы физические основы метода ЭПР?

2. В каких кристаллах можно наблюдать появление сигнала ЭПР?

3. Как можно определить концентрацию парамагнитных центров методом ЭПР?

4. Каков порядок работы на приборе?

Литература

1. Физика твердого тела. Лабораторный практикум./Под ред. А. Ф. Хохлова. М.: Высшая школа, 2001.

2. Альтшулер С. А., Козырев Б. М. Электронный парамагнитный резонанс. М.: Мир, 1961.

3. Пул Г. Техника ЭПР – спектроскопии. М.: Мир, 1970.

4. Федий А. А. Методические указания к проведению основных измерений в ЭПР – спектроскопии. Челябинск, 1985.

ТВЕРДЫЕ ЭЛЕКТРОЛИТЫ

Цель работы: Ознакомиться с теоретическими основами ионного транспорта твердых электролитов, освоить метод измерения ионной электропроводности материалов от температуры; определить энергию активации и величину электропроводности, температуру перехода твердого электролита в суперионное состояние.

ПРОВОДИМОСТЬ ИОННЫХ КРИСТАЛЛОВ

Способность твердых солей и оксидов проводить электрический ток, была известна еще в XIX в. Первые измерения проводимости твердых солей были выполнены ещё Фарадеем. В дальнейшем Варбург, Кюри, Нернст и др. показали, что переносчиком тока в этих веществах являются ионы. Ионная проводимость окислов в то же время нашла первое практическое применение в лампе Нернста, в которой при прохождении электрического тока нагревался стержень, изготовленный из окиси циркония со стабилизирующими добавками. Несмотря на эти успехи, природа ионной проводимости оставалась непонятной. Предполагалось, что она обусловлена диэлектрическим смещением зарядов в пределах молекулы или кристаллической ячейки.

Скачок в понимании механизма проводимости наступил после экспериментальных исследований Иоффе и его учеников, которые установили возможность макроскопического перемещения ионов в кристаллических решетках, доказали выполнение закона Фарадея при электролизе ионных кристаллов. Были определены числа переноса отдельных ионов в различных солях. В 1926 г. природа ионной проводимости твердых тел была объяснена Френкелем, который указал на неизбежность возникновения структурной разупорядоченности кристаллических решеток при температурах, отличных от абсолютного нуля. Идеи Френкеля получили затем развитие в работах Шоттки и Вагнера и легли в основу современных представлений о природе массопереноса в твердых телах.

Во второй половине 60-х годов возникла, и начала интенсивно развиваться новая область электрохимической науки – теория твердях электролитов. Ее появление связанно с открытием кристаллических веществ, обладающих чрезвычайно высокой проводимостью при сравнительно низких температурах, приближающейся к проводимости концентрированных водных растворов (Ag₃SI, AgRbI₅, Na₂O×nAl₂O₃ и др.), а также с успешным применением этих соединений для создания новых типов источников тока, электрохимических датчиков и преобразователей, сверхъемких конденсаторов и т.п.

Все кристаллические ионные проводники можно разделить на три класса, различающиеся по величине проводимости и по механизму её возникновения.

Твердые электролиты(ТЭЛ) с собственной разупорядоченностью (NaCl, КCl и др. вещества), проводимость которых обусловлена присутствием тепловых дефектов Френкеля-Шоттки или небольшого количества примесных ионов. Их электропроводность при небольших температурах не превышает 10^-4 См/м.

Твердые электролитыс примесной разупорядоченностью (например, ZrO₂, содержащий стабилизирующую добавку CaO), у которых структурная разупорядоченность одной из подрешеток обусловлена присутствием достаточного количества посторонних ионо