Изучение явлений самоиндукции и взаимной индукции

ИЗУЧЕНИЕ ЯВЛЕНИЙ САМОИНДУКЦИИ И ВЗАИМНОЙ ИНДУКЦИИ

Лабораторная работа № 9

Разрешено как учебно - методическое пособие для специальностей 1-38 02 01Информационно-измерительная техника

и 1-38 02 03Техническое обеспечение безопасности

Минск

БНТУ

УДК 537.851 (075.8)

ББК 31.292 я7

И39

Составители:

Ю.А. Бумай, В.В. Черный,.

Рецензенты:

И.И. Жолнеревич, П.Г. Кужир

И 39 Изучение явлений самоиндукции и взаимной индукции:

лабораторная работа №9/сост. Ю. А. Бумай [ и др.]. ‒Минск: БНТУ, 2013, 19 с.

Учебно-методическое пособие содержит описание (теоретическую часть, схему экспериментальной установки и задание) лабораторной работы, посвященной изучению явлений самоиндукции и взаимной индукции. иса в ферромагнетиках. На основании полученных результатов определяются величины индуктивностей и коэффициент самоиндукции.

Пособие предназначено для студентов инженерных специальностей, изучающих раздел “ Электричество и магнетизм ” курса общей физики.

УДК 537.851 (075.8)

ББК 31.292 я7

© БНТУ, 2013

ЛАБОРАТОРНАЯ РАБОТА №9

ИЗУЧЕНИЕ ЯВЛЕНИЙ САМОИНДУКЦИИ И ВЗАИМНОЙ ИНДУКЦИИ

Цель работы: изучить закон электромагнитной индукции, явления самоиндукции и взаимной индукции.

Задачи работы:

1. Измерить ЭДС самоиндукции и постоянные времени цепи, содержащей катушку индуктивности, при включении и выключении источника питания.

2. Определить индуктивности и взаимную индуктивность катушек трансформатора

Явление самоиндукции

Предположим, что по некоторому замкнутому контуру протекает ток, сила которого равна I. Ток будет создавать в окружающем пространстве магнитное поле. Силовые линии этого поля будут пересекать также и сам контур и создавать магнитный поток через этот же контур. По закону Био-Савара-Лапласа, модуль вектора магнитной индукции, создаваемой током, будет в любой точке пространства прямо пропорционален силе тока. Следовательно, полный магнитный поток через контур Ψ, называемый иначе потокосцеплением, будет также прямо пропорционален току:

Ψ = L·I, (4)

где L – коэффициент пропорциональности, называемый индуктивностью контура. Индуктивность зависит от формы и размеров контура и магнитных свойств среды, в которой находится контур. Размерность потокосцепления, как и магнитного потока, Вебер. Из (4) следует, что индуктивность численно равна потокосцеплению, пронизывающему контур при силе тока в контуре, равном 1 А. Единица индуктивности в системе СИ называется Генри (Гн): 1Гн = 1 Вб/А = 1 Ом·с.

Индуктивность тонкой длинной катушки (соленоида) длиной l, площадью поперечного сечения S и числом витков N можно определить, используя известную формулу для индукции магнитного поля в соленоиде:

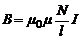, (5)

где μ₀ – магнитная постоянная, μ – относительная магнитная проницаемость среды внутри катушки. Тогда магнитный поток через один виток соленоида

,

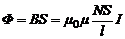а потокосцепление

Ψ = NФ = .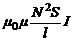

С учетом (4), имеем:

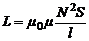. (6)

Строго говоря, последняя формула выражает индуктивность участка бесконечно длинного соленоида длиной l. Конечно, реальные соленоиды имеют конечную длину и индуктивность соленоида меньше. На практике это учитывается введением коэффициента k, значение которого меньше единицы и зависит от соотношения между длиной l соленоида и его радиусом R.

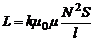. (7)

Как отмечалось, ЭДС индукции возникает в контуре независимо от причин, вызывающих изменение магнитного потока, пронизывающего контур. При изменении тока в контуре изменится и магнитный поток, пересекающий этот контур, что приведет к возникновению в контуре ЭДС индукции. Возникновение ЭДС индукции в проводящем контуре при изменении тока, протекающего по нему, называется явлением самоиндукции. Такое название принято, поскольку ЭДС индукции в контуре возникает в результате изменения тока, протекающего в самом же контуре, а не в результате каких либо внешних воздействий. Величину ЭДС самоиндукции ε_s найдём, если в (3) вместо Ф подставим выражение (4) для Ψ:

ε_s = 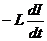(8)

Предполагается, что форма и размеры контура не изменяются, иначе формула усложнится. Знак минус в (8) означает, что ЭДС самоиндукции направлена таким образом, чтобы препятствовать изменению тока в контуре (правило Ленца для ЭДС самоиндукции). Иначе говоря, если ток I возрастает (см. рис. 2,а), то ток I_s, создаваемыйЭДС самоиндукции, направлен против тока в контуре.Если же ток I убывает, ток I_s совпадает по направлению с I (рис 2,б).

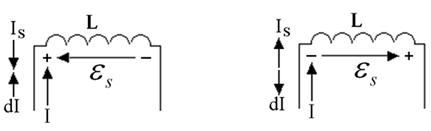а б

Рис.2. Направления токов и ЭДС самоиндукции

Явление взаимной индукции

Пусть имеются два близко расположенных контура. При протекании по одному из них тока изменяется индукция магнитного поля и, следовательно, магнитный поток, пронизывающий второй контур. В результате во втором контуре возникает ЭДС индукции, называемая в данном случае ЭДС взаимоиндукции.

Возникновение ЭДС индукции в одном из двух контуров, связанных магнитной связью, при изменении тока в другом, называется явлением взаимной индукции.

Количественно степень магнитной связи контуров (или любых электрических цепей) характеризуется взаимной индуктивностью.

Пусть ток I₁ течет по первому контуру. Часть данного магнитного потока Ф₁₂ пронизывает второй контур (рис. 3). Величина Ф₁₂ также будет пропорциональна току I₁, т.е.

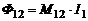, (9)

где 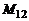- коэффициент, характеризующий влияние первого контура на второй.

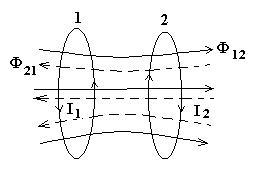
Рис.3. Возникновение ЭДС индукции в одном контуре при изменении тока в другом.

Пусть теперь ток I₂ течет по второму контуру (рис. 3). Рассуждая аналогично предыдущему случаю, для величины магнитного потока, создаваемого током I₂ и пронизывающего первый контур, можно записать:

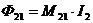
Если отсутствуют ферромагнитные сердечники, коэффициенты 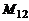и 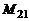тождественно равны и взаимное влияние двух контуров описывается только одним коэффициентом

,

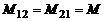который зависит от размеров и формы контуров 1 и 2, от их взаимного расположения, а также от магнитной проницаемости окружающей среды. Данный коэффициент называется взаимной индуктивностью или коэффициентом взаимной индукции контуров 1 и 2 и численно равен величине магнитного потока (в Веберах), общего для двух контуров, когда в одном из них протекает ток, равный 1 А.

При изменении тока в первом контуре, согласно закону электромагнитной индукции, в нем возникает ЭДС самоиндукции:

ε_s1= 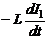(10)

Во втором контуре при этом будет индицироваться ЭДС индукции:

ε_i2 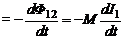(11)

Если второй контур разомкнут, то тока в нём не возникает, следовательно, обратного влияния второго контура на первый не будет. Разделив равенства (10) на (11), получим:

ε_s1 /ε_i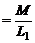2 (12)

Видно, что в любой момент времени отношение ЭДС, которые индуцируются в первом и во втором контуре током, протекающим по первому контуру, постоянно. Следовательно, ЭДС во втором контуре повторяет изменение ЭДС самоиндукции в первом. Это явление используется в трансформаторах для преобразования переменного напряжения в более низкое или в более высокое. Отношение М/L₁ называется КОЭФФИЦИЕНТОМ ТРАНСФОРМАЦИИ.

КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. Что такое поток магнитной индукции?

2. Сформулируйте закон электромагнитной индукции Фарадея и правило Ленца.

3. Что такое явления самоиндукции и взаимной индукции?

4. Что такое индуктивность и от чего зависит величина индуктивности катушки?

5. Почему при замыкании и размыкании цепи величина напряжения на катушке различна?

6. Чем определяется длительность нарастания и спада в цепи с индуктивностью?

Литература

1. Савельев И.В. Курс общей физики. В 3-х т. Т.2,М., «Наука», 1988, с.181 – 195.

2. Савельев И.В. Курс физики. В 3-х т. Т.2, М., «Наука», 1989, с. 196 –- 211.

3. Трофимова Т.И. Курс физики. М.:ВШ, 2007, с. 221 – 233.

4. Наркевич И.И., Волмянский Э.И., Лобко С.И. Физика. – Мн.: Новое знание, 2004, с. 386 – 393.

5. Детлаф А.А., Яворский Б.М. Курс физики. М.:ВШ, 2007, с. 328 – 340.

6. Путилов К.А. Курс физики. В 3-х т. Т.2, М.: «Физматгиз», 1963, изд. 6-е, с. 372 – 395

[1] Примечание. При измерениях ЭДС и постоянных времени результат измерения определяйте путём умножения коэффициентов отклонения или развёртки на линейные размеры измеряемых параметров сигнала, выраженные в делениях шкалы

ИЗУЧЕНИЕ ЯВЛЕНИЙ САМОИНДУКЦИИ И ВЗАИМНОЙ ИНДУКЦИИ

Лабораторная работа № 9

Разрешено как учебно - методическое пособие для специальностей 1-38 02 01Информационно-измерительная техника

и 1-38 02 03Техническое обеспечение безопасности

Минск

БНТУ

УДК 537.851 (075.8)

ББК 31.292 я7

И39

Составители:

Ю.А. Бумай, В.В. Черный,.

Рецензенты:

И.И. Жолнеревич, П.Г. Кужир

И 39 Изучение явлений самоиндукции и взаимной индукции:

лабораторная работа №9/сост. Ю. А. Бумай [ и др.]. ‒Минск: БНТУ, 2013, 19 с.

Учебно-методическое пособие содержит описание (теоретическую часть, схему экспериментальной установки и задание) лабораторной работы, посвященной изучению явлений самоиндукции и взаимной индукции. иса в ферромагнетиках. На основании полученных результатов определяются величины индуктивностей и коэффициент самоиндукции.

Пособие предназначено для студентов инженерных специальностей, изучающих раздел “ Электричество и магнетизм ” курса общей физики.

УДК 537.851 (075.8)

ББК 31.292 я7

© БНТУ, 2013

ЛАБОРАТОРНАЯ РАБОТА №9