Измерение физических величин

ИЗМЕРЕНИЕ ФИЗИЧЕСКИХ ВЕЛИЧИН

Курс физики составляет основу теоретической и экспериментальной подготовок инженера любого профиля, без которой невозможна его успешная деятельность. Одна из задач, которая ставится перед будущими инженерами, - это овладение приемами и методами постановки физического эксперимента и обработка полученных результатов. Численные значения могут быть использованы лишь в том случае, если они достоверны. Однако любая величина может быть измерена лишь с некоторой, определяемой разными факторами точностью.

Ошибка измерения данной физической величины Δх представляет собой модуль разности между результатом измерения х и истинным значением А измеряемой величины, т.е. .

Истинное значение А физической величины, т.е. абсолютное ее значение, невозможно получить. Следовательно, неизвестна ошибка ее измерения .

Поэтому основной задачей математической обработки результатов измерений является нахождение числового интервала, в котором может находиться истинное значение А измеряемой физической величины с определенной вероятностью.

ВЕРОЯТНОСТЬ СОБЫТИЯ

Под событием В понимается всякое происходящее явление. На­пример, попадание в цель при выстреле. Событие называется достовер­ным, если оно должно произойти непременно, и, наоборот, событие на­зывается невозможным, если оно заведомо не наступит.

Допустим, имеется возможность неограниченного повторения ис­пытаний, в каждом из которых при сохранении неизменных условий отмечается появление или непоявление события В. Например, из 10 выстрелов (n) 7 выстрелов (Δn) попали в цель. Отношение принято называть частотой события В, т.е.

Р(В) = = 0,7. (1)

Из выражения (1) видно, что вероятность достоверного события Р(В) = 1 при Δn = n, а невозможного Р(В) = 0 при Δn = 0. Таким образом, 0 < Р(В) < 1 при 0 < Δn < n.

РАСПРЕДЕЛЕНИЕ СЛУЧАЙНЫХ ОШИБОК ИЗМЕРЕНИЯ.

ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ И ДОВЕРИТЕЛЬНАЯ

ВЕРОЯТНОСТЬ

При неоднократном измерении одной и той же величины x ре­зультаты отдельных измерений х_1, х₂...х_n будут неодинаковы из-за наличия случайных ошибок.

В курсе математической статистики доказывается, что наилучшей оценкой истинного значения А измеряемой величины х является ее среднее арифметическое значение:

, (2)

где n – число измерений; - результат отдельного измерения величины А.

Ошибка нам тоже неизвестна, поэтому имеется какая-то вероятность того, что истинное значение А лежит в некоторых пределах вблизи . Важно найти эти пределы или интервал, в пределах которого с заданной вероятностью обнаружится значение определяемой величины А. Для этого выбирают некоторую вероятность α, близкую к 1, и определяют для нее интервал от до , в котором бы находилось значение определяемой величины. Этот интервал называется доверительным интервалом, а вероятность α - доверительной вероятностью, - доверительная граница общей погрешности измерений.

Поясним смысл терминов: доверительная граница общей погрешности и доверительная вероятность α. Для этого используем числовую ось.

Пусть среднее значение измеряемой величины – (рис.1). Отложим от справа и слева. Полученный числовой интервал от до называется доверительным интервалом.

Рис. 1

Результаты ряда измерений можно наглядно представить в виде диаграммы, которая показывает, как часто получаются те или иные значения. Такая диаграмма называется гистограммой.

Чтобы построить гистограмму, надо весь диапазон измеренных значений от x_min до х_max разбить на равные интервалы (рис. 2) и подсчитать относительную частоту Δn/n попаданий результатов измерения в каждый интервал (n – число всех измерений, Δn – число измерений, попадающих в данный интервал).

Рис. 2	Рис. 3

Если увеличить число измерений, ступенчатая кривая будет приближаться к гладкой кривой, которая называется кривой распределения случайной величины x_i. Величина f(x), пропорциональна доле числа отсчетов Δn/n, попадающей в каждый интервал. Она называется плотностью вероятности.

Смысл плотности вероятности заключается в том, что произведение f(x)dx дает долю полного числа отсчетов n, приходящуюся на интервал от x до x+dx или, иначе говоря, вероятность того, что результат любого отдельного измерения х_i будет иметь значение, лежащее в указанном интервале. Эта вероятность численно равна площади заштрихованной криволинейной трапеции ΔS.

Вся площадь под кривой распределения определяется как произ­ведение вероятности попадания измеренного значения на всю числовую ось х и равна 1, т.е.

,

где Р(х) – функция распределения случайной величины х.

Математически закон распределения случайной величины х выражается законом Гаусса (нормальный закон распределения) и имеет вид

f(x)= (3)

где f(x) – функция плотности вероятности; е – основание натурального логарифма; х – результат очередного измерения; А – истинное значение измеряемой величины; ² – дисперсия, которая определяется по формуле

.

Поскольку дисперсия имеет размерность квадрата случайной величины, а это не всегда удобно, то вводится средняя квадратичная ошибка , которая представляет собой положительный квадратный корень из дисперсии:

.

Если средняя квадратичная ошибка неизвестна, то вместо нее используют величину S( ) - среднее квадратичное отклонение среднего результата.

. (4)

Как видно из выражения (3), функция плотности вероятности для распределения Гаусса является функцией двух параметров – А и σ. Распределение Гаусса симметрично относительно А (или ), его ширина пропорциональна σ (рис.4). Чем точнее измерения, тем плотнее вблизи среднего значения лежат результаты отдельных измерений, т.е. величина σ меньше. С уменьшением σ фигура, образуемая кривой распределения, сужается и вытягивается вверх. При этом площади под кривыми распределения будут равны между собой, т.к. вероятность попадания случайной величины на всю числовую ось равна 1. С увеличением числа измерений S( ) стремится к средней квадратичной ошибке

Рис. 4

Следовательно, S( ) является приближенным значением средней квадратичной ошибки σ, т.е. ее оценкой, которая тем ближе к σ, чем больше число измерений. Из формулы (4) следует, что с увеличением числа измерений средняя квадратичная ошибка изменяется обратно пропорционально корню квадратному из числа измерений. Однако в действительности существует предел

уменьшения средней квадратичной ошибки за счет увеличения числа измерений. Существование этого предела обусловлено наличием систематических ошибок, которые в действительности всегда существуют и не изменяются при увеличении числа измерений. Поэтому обычно производят небольшое (5-6) число измерений.

Задаваясь определенной доверительной вероятностью α, можно определить отношение доверительной границы случайной погрешности ε к среднему квадратичному отклонению S( ), т.е. найти

Отношение называется коэффициентом Стьюдента, который не зависит от среднего квадратичного отклонения, а зависит лишь от вы­бора доверительной вероятности и числа измерений n. Это позволило Стьюденту составить таблицу значений коэффициентов (табл. 1).

МАЯТНИКЕ ОБЕРБЕКА

Цель работы: исследование зависимость момента инерции маятника от расположения грузов, закрепленных на стержне маятника.

Приборы и принадлежности: маятник Обербека, набор грузов и перегрузов, штангенциркуль.

Теоретические сведения

В механике под твердым телом подразумевают абсолютно твердое тело, т. е. тело деформациями которого можно пренебречь. При вращении твердого тела все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. Быстроту вращения характеризуют углом поворота тела в единицы времени. Если за любые равные промежутки времени тело поворачивается на одинаковые углы, вращение называется равномерным. Величина, определяющая изменение угла поворота за единицу времени, называется угловой скоростью. Угловая скорость определяется по формуле

.

Единицей измерения угловой скорости является рад/с. При неравномерном вращении изменение угловой скорости со временем характеризуется угловым ускорением, которое вычисляется по формуле

.

Единица измерения углового ускорения является рад/с². Угловая скорость ω и угловое ускорение ε связаны с линейной скоростью и линейным (тангенциальным) ускорением следующими соотношениям:

и , (1)

где –расстояние от точек до оси вращения

При вращении тела вокруг неподвижной оси изменение угловой скорости и его движения зависит от действующего момента силы. Моментом силы относительно неподвижной точки О называется векторная величина, определяемая векторным произведением радиуса-вектора , проведенного из точки О в точку Априложения силы, на силу (рис. 1).

,

где –псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от к .

Рис. 1	Рис.2

Модуль момента силы

,

где –угол между и ; –плечо силы - кратчайшее расстояние между линиями действия силы и точкой О.

Моментом силы относительно неподвижной оси ,называется скалярная величина , равная проекции на эту ось вектора момента силы , определенного относительно произвольной точки О, данной на оси (рис. 2). Значение момента не зависит от выбора положения точки О на оси .

Равнопеременное вращательное движение тел характеризуется постоян­ным угловым ускорением, оно появляется под действием сил, момент которых постоянен по величине и направлению.

Зависимость углового ускорения от момента силы выражена в основном законе динамики вращательного движения

, (2)

где - момент инерции тела.

Момент инерции материальной точки относительно какой-либо оси вращения называется скалярная величина, равная произведению массы m этой точки на квадрат расстояния от точки до оси вращения:

.

Моментом инерции тела относительно данной оси вращения называют сумму моментов инерции элементарных масс, на которые разбивается тело:

,

где - элементарная масса; - расстояние от элементарной массы до оси вращения.

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела относительно любой оси вращения равен моменту инерции относительно параллельной оси, проходящей через центр масс тела, сложенному с произведением массы тела на квадрат расстояния между осями:

.

Законы вращения тел можно изучить с помощью маятника Обербека.

Рис.3

Рассмотрим движения механической системы представленной на рис. 3. Груз массой m движется с ускорением под действием результирующей силы тяжести и силы натяжения нити (рис. 3). Запишем для груза второй закон Ньютона в проекции на направление движения: Диск вращается равноускоренно под действием натянутой нити, вызванной силой натяжения нити . Сила натяжения передается нитью от груза к диску вращающегося маятника.

Если предположить, что нить невесомая, то на диск маятника действует сила , равная по величине и противоположная ей по направлению (следствие третьего закона Ньютона: ). Отсюда

. (3)

Сила натяжения нити создает вращательный момент относительно горизонтальной оси O, направленный вдоль этой оси «от нас» и приводящий в движение маятник Обербека. Величина момента силы равна

, (4)

где – радиус диска, на который намотана нить.

Основной закон динамики вращательного движения (2) в скалярном виде и с учетом момента силы (4) примет вид (записаны проекции векторов моментов сил и углового ускорения на ось вращения О,направление которой выбрано «от нас»):

. (5)

Используя кинематическую связь линейного и углового ускорения (1), а также уравнение движения груза при нулевой начальной скорости , выразим через величины и :

. (6)

Преобразуем уравнение (5), используя выражение (6) и и получим момент инерции маятника Обербека

. (7)

Эту зависимость можно использовать для экспериментальной оценки величины момента инерции маятника Обербека.

Теоретический расчет момента инерции маятника Обербека представляет сумму моментов инерций - момента инерции диска радиусом , - моментов инерции четырех подвижных грузов и - момента инерции крестовины маятника без груза .

.

В связи с тем, что размеры грузов малы по сравнению с расстоянием от оси вращения до центров масс грузов, то грузы можно считать материальными точками. Для материальной точки момент инерции равен

,

где – масса груза на крестовине; – расстояние от оси вращения до центра грузов. Момент инерции крестовины маятника без груза определяется как

,

где – масса стержня без груза; - длина стержня крестовины.

Таким образом, теоретический расчет момент инерции маятника можно представить следующей формулой

.

Расчет разности моментов инерции и для двух различных расстояний и позволит исключить слагаемые и . Тогда теоретический расчет момента инерции маятника будет определяться по формуле

. (8)

Расчет момента инерции маятника по формуле (7) при различных расположениях грузов на крестовине можно теоретически проверить величиной момента инерции , рассчитанного по формуле (8).

Описание установки

Для расчетов экспериментального и теоретического моментов инерции представлена установка маятника Обербека (рис. 4, а). Схематический вид установки маятника Обербека показан на рис. 4, б, в.

Маятник Обербека имеет вертикальную колонну 1, которая установлена на основании 2. На вертикальной колонне 1 прикреплены два кронштейна: нижний 3 является неподвижным, верхний 4 - подвижный и две неподвижные втулки: нижняя 5 и верхняя 6. Основание снабжено регулируемыми ножками 7, обеспечивающими горизонтальную установку прибора.

На верхней втулке 6 посредством основания 8 закреплен подшипниковый узел диска 9 и диск 10. Через диск перекидывается нить 11. Один конец нити прикреплен к двухступенчатому диску 12, а на втором конце закреплены грузы 13. На нижней втулке 5 посредством основания 14 прикреплен тормозной электромагнит 15, который удерживает систему крестовины вместе с грузами в состоянии покоя. Подвижный кронштейн 4 можно переместить вдоль колонны и фиксировать его в любом положении, определяя длину пути падающего груза. Для этого на колонне 1 нанесена миллиметровая шкала 16. На подвижном кронштейне 4 укреплен фотоэлектрический датчик 17. На неподвижном кронштейне 3 - фотоэлектрический датчик 18. К кронштейну 3 прикреплен кронштейн 19 с резиновым амортизатором, ограничивающим движение грузов.

Под действием груза нить разматывается и приводит маятник во вращательное движение, которое предполагается равноускоренным. Угловое ускорение при этом тем меньше, чем больше момент инерции системы относительно оси вращения, величина которого зависит от положения перемещаемых грузов на крестовине. Время движения груза измеряется электронным секундомером 18, расположенным у основания прибора, а остановка происходит по сигналу фотодатчика. Груз опускается на расстояние , измеряемое вертикально закрепленной линейкой с сантиметровыми делениями.

а	б	в
Рис. 4

Порядок выполнения работы

1. Установить один перегруз на падающий груз. Определить массу общего падающего груза и записать в табл.

2. Измерить с помощью штангенциркуля диаметр диска. Рассчитайте радиус диска и записать в табл..

3. Укрепить на стержне крестовины грузы на одинаковых расстояниях от оси вращения (в пределах от 5 до 15 см). Определите это расстояние, используя деления нанесенные на стержне (1 деление =1 см) и записать в табл.

4. Вращая маятник рукой, намотать нить на диск и установить падающий груз на высоте (в пределах от 30 до 40 см). Значение высоты записать в таб.

5. Включить электронный секундомер. Нажать кнопку «пуск» и одновременно запустить вращение диска. В момент прохождения грузом нижней точки секундомер остановится. Записать время падения груза в табл.

6. Провести прямые пятикратные измерения времени падения груза при неизменной геометрии эксперимента согласно п.п. 4-5. Результаты измерений записать в табл. Рассчитать среднее время падения.

7. Изменить расстояние от оси вращения до грузов (в пределах от 20 до 25 см) и записать в табл.

8. Провести прямые пятикратные измерения времени падения груза при неизменной геометрии эксперимента согласно п.п. 4-5. Результаты измерений записать в табл. Рассчитать среднее время падения.

Таблица

N	, г	, г	, см	, см	, см	, c	, см	, c
	=	=

9. Вычислить экспериментальные значения моментов инерции маятника и с грузами на стержнях, расположенных на разном расстоянии от оси вращения по формуле (7). В качестве времени падения груза взять его среднее значение.

10. Рассчитать теоретическое значение момента инерции маятника для выбранных расстояний по формуле (8).

11. Сравнить полученные результаты и найдите относительную погрешность измерения момента инерции по формуле

,

где - теоретическое изменение моментов инерции при разных расстояниях; - экспериментальное изменение моментов инерции при разных расстояниях.

Контрольные вопросы

1. Дать определение абсолютно твердого тела и вращательного движения.

2. Дать определение средней и мгновенной угловых скоростей, средней и мгновенной угловых ускорений. Единицы измерения угловой скорости и углового ускорения. Как определяется направления векторов угловой скорости и углового ускорения? Какова связь между линейными и угловыми скоростями и ускорениями?

3. Почему движение падающего груза и вращение маховика являются равноускоренными?

4. Вывести основной закон динамики вращательного движения.

5. Что называется моментом силы тела относительно неподвижной точки вращения? Как определяется его направление? В каких единицах он измеряется?

6. Какая сила сообщает вращающий момент маятнику? Как направлен момент этой силы?

7. Что называется моментом инерции материальной точки и тела? В каких единицах он измеряется? Каков физический смысл момента инерции тела.

8. Сформулируйте и объясните теорему Штейнера.

ЛАБОРАТОРНАЯ РАБОТА №6

ЛАБОРАТОРНАЯ РАБОТА №10

ЦИКЛ КАРНО

Цель работы: изучение работы идеальной машины Карно.

Приборы и принадлежности: компьютер, CD-диск "Открытая физика"

Теоретические сведения

Основной темой термодинамики, во времена ее формирования как науки, являлось превращение теплоты в работу.

Поэтому все полученные закономерности основаны на обобщении опыта по созданию многочисленных тепловых машин и вечного двигателя (перпетуум-мобиле). Эти выводы сформулированы в виде основных законов (начал) термодинамики.

С одной стороны, первое начало термодинамики гласит о том, что количество теплоты, сообщаемое системе, затрачивается на приращение внутренней энергии системы и совершение системой работы над внешними телами:

.

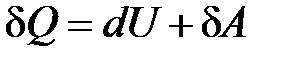С другой стороны, это говорит о том, что вечный двигатель первого рода, т.е. такой периодически действующий двигатель, который совершал бы работу в большем количестве, чем получаемая им извне энергия, невозможен.

Из этого следует то, что тепловой двигатель лишь получает извне тепловую энергию, совершая при этом какую-то механическую работу. Причем из определения двигателя следует также, что данное превращение должно происходить многократно и без изменений в конструкции двигателя.

Другими словами, всякий двигатель представляет собой систему, многократно совершающую некий круговой процесс (цикл).

Круговым процессом (циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное.

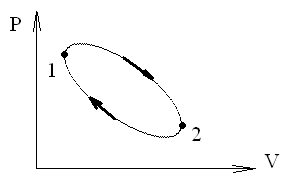Рис. 1

Рассмотрим цикл, совершаемый некоторой тепловой машиной, рабочим телом в которой является идеальный газ (рис. 1). Этот цикл можно разбить на два процесса: (1-2) – расширение; (2-1) – сжатие. Напомним, что площадь под кривой на этом графике соответствует работе газов. Из рисунка видно, что, во-первых, работа расширения (1-2) положительна, а работа (2-1) сжатия – отрицательна.

Во-вторых, работа расширения (площадь под кривой (1-2)) больше, чем работа сжатия (площадь под кривой (2-1)). Из этого следует, что общая работа за весь цикл будет больше нуля.

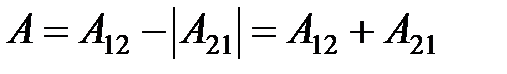>0,

где А – работа за весь цикл, А₁₂, А₂₁ – работа газа, затрачиваемая на расширение и сжатие соответственно.

Если за цикл совершается положительная работа (цикл протекает по часовой стрелке), то он называется прямым, а если отрицательная (цикл протекает против часовой стрелки) – обратным.

Процесс (1-2) (рис.1) происходит благодаря получению извне теплоты Q₁, а процесс (2-1) сопровождается потерей теплоты Q₂. Совершаемую работу вычисляют как

.

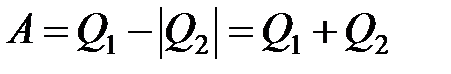КПД определяют как

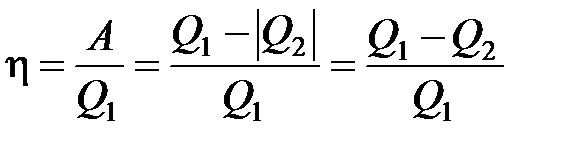. (1)

Из рис. 1 следует, что т.к. тепловая машина работает по циклу, то процесс (2-1) необходим для возвращения рабочего тела в исходное состояние. И этот процесс сопровождается потерей теплоты Q₂. Следовательно, КПД не может быть равным 1.

Поэтому второе начало термодинамики в одной из формулировок гласит: невозможен вечный двигатель второго рода, т.е. такой периодически действующий двигатель, который получал бы тепло от одного резервуара и превращал это тепло полностью в работу.

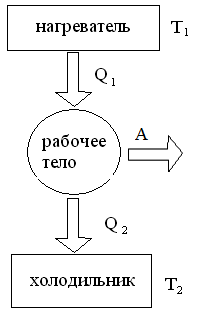Рис. 2

Другими словами, теплота Q2 теряется не из-за несовершенства конструкции теплового двигателя, а из-за того, что требуется энергия для возвращения рабочего тела (идеального газа) в первоначальное состояние (состояние 1 на рис. 1). Поэтому для функционирования тепловой машины необходимо наличие двух тепловых резервуаров. От одного из них, имеющего более высокую температуру Т1 и называемого нагревателем, двигатель получает в ходе цикла теплоту Q1, а второму, имеющему более низкую температуру Т2 и называемому холодильником, двигатель отдает тепло Q2 (рис. 2).

Основываясь на втором начале термодинамики, французский физик и инженер Сади Карно (1796-1832) вывел теорему, носящую теперь его имя. Она гласит: из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей и холодильников, наибольшим КПД обладают обратимые машины; при этом КПД машин, работающих при одинаковых температурах нагревателей и холодильников, равны друг другу и не зависят от природы рабочего тела.

Карно рассмотрел наиболее экономичный обратимый цикл, состоящий из двух изотерм и двух адиабат, и называемый циклом Карно. Рассмотрев прямой цикл с идеальным газом в качестве рабочего тела, он вывел формулу расчета КПД данной машины (идеальной машины, машины Карно):

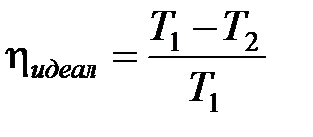. (2)

Причем теплота Q₁ равна работе А₁₂, совершенной после первого изотермического расширения газа от объема V₁ до объема V₂ , и может быть найдена по формуле

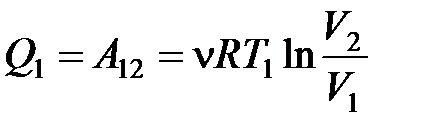. (3)

Исходя из формул (1), (2) и (3) возможно найти работу А, совершаемую газом за весь цикл:

А = η Q₁. (4)

Цикл Карно графически представлен на рис. 3:

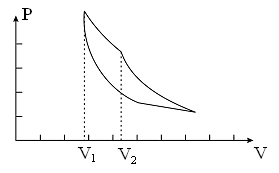
Рис. 3

Порядок выполнения работы

1. Включить компьютер.

2. Найти на рабочем столе компьютера ярлык "Открытая физика" и двойным нажатием левой кнопки мыши войти в программу.

3. Выбрать раздел "Молекулярная физика" и войти в раздел щелчком левой кнопки мыши (или нажав клавишу "Enter").

4. В открывшемся окне с помощью мыши или вертикальных стрелок на клавиатуре выбрать демонстрацию "Цикл Карно" и открыть ее щелчком левой кнопки мыши.

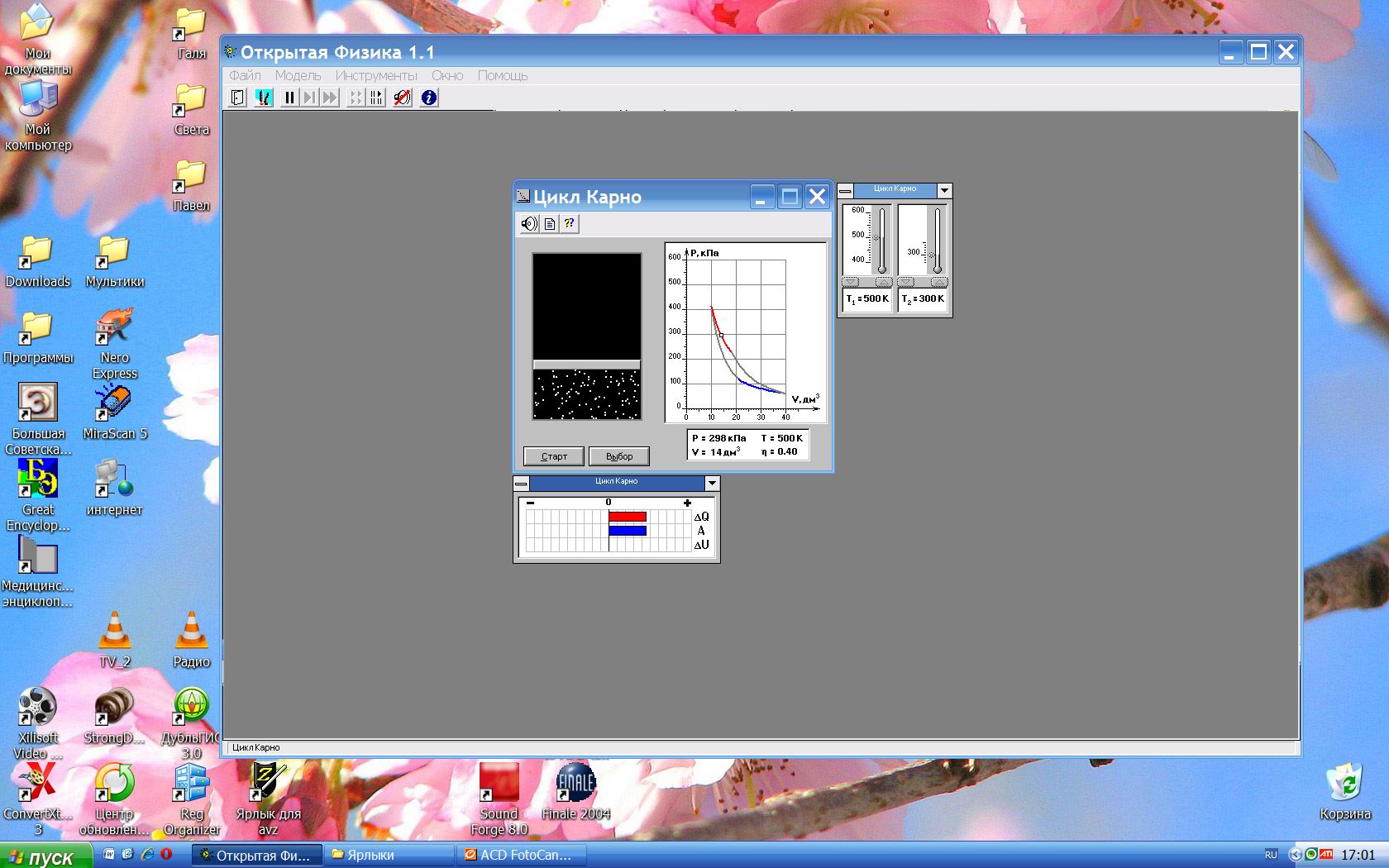
Рис. 4

5. В образовавшемся окне (рис. 4) вы можете изначально установить параметры цикла Карно.

6. Нажмите кнопку «Выбор». С помощью кнопок задать температуру Т₁ (температуру нагревателя). Нажать кнопку «Старт». Внесите в табл. результаты опыта (Т₁ и 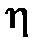). Зарисовать с экрана график цикла Карно.

7. Повторите пункт 6 еще два раза, задав различные значения Т₁. Зарисовать с экрана график цикла Карно.

Таблица

Т1, К	Т2, К	V1, м3	V2, м3		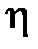Q1, Дж	A, Дж

8. Нажмите кнопку «Выбор». С помощью кнопок задать температуру Т₂ (температуру холодильника). Нажать кнопку «Старт». Внесите в табл. результаты опыта. Зарисовать с экрана график цикла Карно.

9. Повторите пункт 8 еще два раза, задав различные значения Т₂. Зарисовать с экрана график цикла Карно.

11. Рассчитать по формулам 3 и 4 значения Q₁ и A для количества вещества 1 моль.

12. Сделать выводы по проделанной работе.

Контрольные вопросы

1. Какие процессы называют обратимыми? Равновесными?

2. Что такое циклический процесс? Цикл тепловой и холодильной машины, в чем различие?

3. Дать определение первому началу термодинамики.

4. Что такое энтропия? Как она изменяется при различных процессах? Что такое «Тепловая смерть Вселенной»?

5. Дать определение второму началу термодинамики.

6. Вечный двигатель 1-го и 2-го рода. Охарактеризовать причины их невозможности.

7. Тепловая машина, ее принципиальное устройство и КПД.

8. Как изменится КПД тепловой машины, если увеличить температуру нагревателя?

9. Как изменится КПД тепловой машины, если увеличить температуру холодильника?

10. Теорема Карно. Машина Карно и ее КПД.

ЛАБОРАТОРНАЯ РАБОТА №11

ИЗМЕРЕНИЕ ФИЗИЧЕСКИХ ВЕЛИЧИН

Курс физики составляет основу теоретической и экспериментальной подготовок инженера любого профиля, без которой невозможна его успешная деятельность. Одна из задач, которая ставится перед будущими инженерами, - это овладение приемами и методами постановки физического эксперимента и обработка полученных результатов. Численные значения могут быть использованы лишь в том случае, если они достоверны. Однако любая величина может быть измерена лишь с некоторой, определяемой разными факторами точностью.

Ошибка измерения данной физической величины Δх представляет собой модуль разности между результатом измерения х и истинным значением А измеряемой величины, т.е. .

Истинное значение А физической величины, т.е. абсолютное ее значение, невозможно получить. Следовательно, неизвестна ошибка ее измерения .

Поэтому основной задачей математической обработки результатов измерений является нахожде