Изучение принципа суперпозиции магнитных полей.

ОПРЕДЕЛЕНИЕ ГОРИЗОНТАЛЪНОЙ СОСТАВЛЯЮЩЕЙ ИНДУКЦИИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ

Цель работы: Изучить принцип суперпозиции магнитных полей на примере определения горизонтальной составляющей магнитного поля Земли.

Приборы и принадлежности: Источник постоянного тока (G4), тангенс-гальванометр {тг), амперметр(А), переключатель (S2), реостат (R 14).

Теоретическое введение

Земля представляет собой огромный магнит, который в окружающем Землю пространстве создаст магнитное поле. Магнитные полюсы Земли не совпадают с географическими полюсами и со временем изменяют свое положение. Вектор индукции магнитного поля в Земли на экваторе направлен горизонтально, у магнитных полюсов Земли - вертикально и всюду в других местах- под некоторым углом кгоризонтальной плоскости. Направление вектора магнитной индукции поля Земли можно определить с помощью магнит­ной стрелки NS, подвешенной на тонкой нити (рисунок 1). Магнитная стрелка устанавливается по направлению вектора 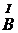. Вертикальная плоскость, в которой установится стрелка, называется плоскостью магнитного меридиана. Так как магнитные полюса не совпадают с географическими, то стрелка будет отклонена от географического меридиана на некоторый угол α, который называют магнитным склонение. На рисунке 1 угол магнитного склонения представлен как угол между плоскостями магнитного и географического меридианов. Угол, который образует магнитная стрелка с горизонтальной линией, лежащей в плоскости магнитного меридиана называют магнитным наклонением .

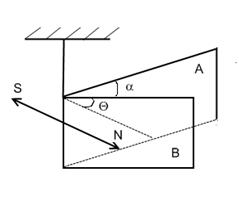
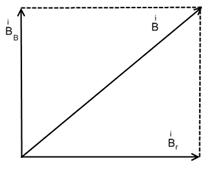
Рисунок 1 Рисунок 2

А- плоскость географического меридиана Для случая, когда плоскость,

В- плоскость магнитного меридиана. магнитного меридиана совпа-

дает с плоскостью ZOY.

Вектор индукции 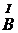магнитного поля Земли можно разложить на две составляющие: горизонтальную 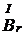и вертикальную 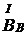(рисунок 2). Величины 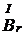, 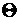, - называют элементами земного магнетизма.

Если магнитная стрелка может вращаться только вокруг вертикальной оси, то она будет устанавливаться лишь под действием 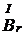. Это свойство используется для определения величины 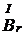, с помощью специального прибора называемого тангенс-гальванометром.

Тангенс-гальванометр представляет собой плоский вертикальный виток радиуса R, в центре которого в горизонтальной плоскости расположена магнитная стрелка, способная вращаться только вокруг вертикальной оси (рисунок 3а). Выберем прямоугольную систему координат таким образом, чтобы плоскость витка совпадала с плоскостью ZOY, лежащей в плоскости магнитного меридиана, а магнитная стрелка NS вращалась вокруг вертикальной оси, помещенной в точке О, при этом плоскость вращения магнитной стрелки совпадает с плоскостью XYZ. При отсутствии тока в витке стрелка устанавливается в плоскости магнитного меридиана ZOY. При пропускании тока по витку в центре его возникает магнитное поле, вели­чину индукции которого можно определить, используя закон Био-Савара- Лапласа общем виде:

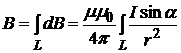, (1)

где L - длина проводника произвольной формы, r - расстояние от точки пространства, где определяется поле dB до элемента проводника dL создающего это поле, I - ток проводника,  - угол между направлениями тока I и радиуса вектора r, μ - относительная магнитная проницаемость среды (для воздуха μ=1), μ - магнитная постоянная равная 4π10^-7 Г/м.

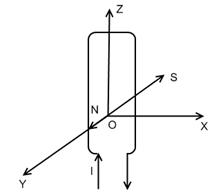
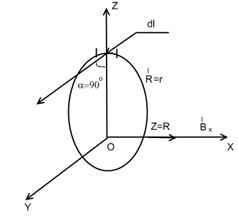
Рисунок 3а Рисунок 3б

Дня случая кругового тока  = 90^о, r = R (где R - радиус витка) имеют постоянные значения для всех участков dL (рисунок 3 б). Длина проводника в этом случае L = 2πR. Поэтому, в соответствии с формулой (1) индукция магнитного поля В в центре кругового тока равна:

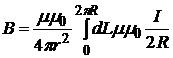. (2)

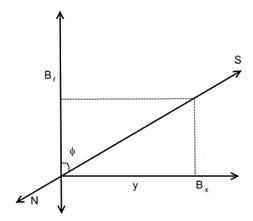
Под действием индукции 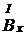магнитная стрелка повернется на некоторый угол φ, устанавливаясь в направлении равнодействующей индукции двух поле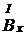й и 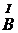рисунок 4. Из рисунка 4 видно, что

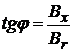или ,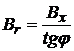

подставляя в это уравнение значение 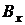, из уравнения (2) получим:

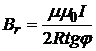. (3)

Зная величины тока I и угла φ можно определить значение 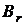. Если вместо одного витка с током I взять короткую катушку, состоящую из n витков, то величина 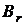, будет в n раз больше

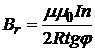Рисунок 4

, (4)

где R=100 мм - радиус, n = 10 - число витков.

Порядок выполнения работы

1.Собрать рабочую схему.

2.Проверить тангенс-гальванометр, установить плоскость катушки тангенс - гальванометра в плоскости магнитного меридиана, при этом один конец магнитной стрелки совпадает с 0^о на круговой шкале компаса.

3.Включают постоянный ток и ставят ползунок реостата так, чтобы стрелка компаса показывала Х^о и записывают значение силы тока I₁. Не меняя величину угла, переключателем меняют направление тока и измеряют величину тока I₂.

4.Аналогично проделать опыты при двух различных углах.

5.По формуле (4) найти величину горизонтальной составляющей индукции магнитного поля Земли для всех случаев и найти среднее.

6.Результаты измерений записать в таблицу.

7.Определить абсолютную и относительную погрешности.

8.Из формулы 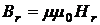, определить горизонтальную составляющую напряженности магнитного поля Земли.

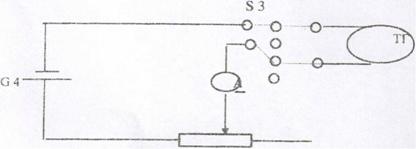
Рабочая схема

Таблица измерений

№ п/п		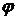I1 (А)	I2 (А)	Iср (А)	tg	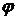Br (Тл)		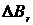Hr	E %
Ср.

Контрольные вопросы

1. Магнитное поле, условие его возникновения. Магнитная индукция. Напряженность магнитного поля. Связь между ними.

2. Закон Био-Савара-Лапласа в дифференциальном виде.

3. Вывести формулу индукции магнитного поля в центре кругового тока. Показать направление вектора индукции.

4.Дать понятия элементов земного магнетизма.

5.Указать факторы, влияющие на величину индукции магнитного поля Земли.

ЛАБОРАТОРНАЯ РАБОТА