Исследование неупругого удара с помощью баллистического маятника

Цель работы: 1) пользуясь законами сохранения энергии и импульса определить скорость пули и работу деформации.

Оборудование: баллистический маятник, пружинный пистолет, пуля, шкала отсчета, линейка, секундомер.

Теоретическое введение

Баллистический маятник представляет собой цилиндр, заполненный пластилином, и подвешенный на четырех длинных нитях к потолку(Рисунок 1). Под цилиндром помещается шкала отсчета. Пружинный пистолет закрепляется специальным зажимом.

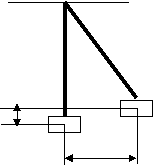1. После выстрела пуля массой m и со скоростью υ застревает в пластилине и продолжает движение с цилиндром со скоростью u. На основании закона сохранения импульса имеем:

mυ = (m + M)u, (1)

где υ - скорость пули до удара, L

u - скорость пули с цилиндром

после удара, M - масса цилиндра. Н

При отклонении маятника в край-

нее положение, его кинетическая S

энергия переходит в потенциальную. Рисунок 1

(m + M)u²/2 = (m + M)gH, (2)

отсюда

u² = 2gH. (3)

Из рисунка 1 (при L >> H и малом угле α ) можно найти

H=S² / 2 L, (4)

где S – горизонтальное перемещение цилиндра вдоль шкалы,

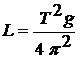. (5)

Решая совместно (1), (3), 4) и (5) найдем скорость пули:

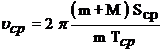. (6)

Относительная погрешность определения скорости рассчитывается по формуле

(7)

Абсолютную погрешность 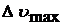определим:

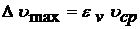. (8)

Считая удар пули о пластилин в цилиндре центральным неупругим ударом, а систему неизолированной, можно записать на основании закона сохранения энергии

mυ²/2 = (m + M)u²/2 + A, (9)

где A - энергия, затрачиваемая на деформацию тела, т.е. работа деформации. Решая совместно (1) и (8) найдем работу деформации

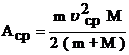, (10)

где υ - скорость пули, определяемая по формуле (6).

Абсолютную погрешность для работы деформации можно рассчитать по формуле

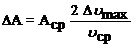. (11)

Порядок выполнения работы

1. Отметить на шкале положение стрелки при неподвижном цилиндре.

2. Зарядить пистолет.

3. Произвести выстрел и отметить положение стрелки при максималь­ном отбросе цилиндра. Одновременно с помощью секундомера заметить вре­мя 10 полных колебаний. Опыт произвести не менее 5 раз. Результаты за­нести в таблицу.

4. Из 10 полных колебаний определить период маятника T = t/10 для каждого опыта.

5. Подсчитав S_ср, Т_ср определить среднюю скорость пули υ_ср. по формуле (6) и работу деформации A_ср по формуле (10). Рассчитать погрешности определения этих величин по формулам (7), (8) и (11).

6. Окончательный результат записать в виде

υ = υ_ср ± Dυ_MAX, A= A_ср ± DA.

Таблица измерений

№ п/п	Si [м]	DS=|Si-Sср| [м]	ti (c)	Ti (c)	DT=|Ti-Tср| (c)	υср (м/c)	A (Дж)
1. 2. 3. 4. 5.
сумма
сред. знач.

Контрольные вопросы

1.Сформулируйте и запишите закон сохранения импульса и закон сохранения энергии.

2. Какая система называется изолированной ?

3. Что такое импульс тела, импульс силы ?

4. Напишите формулу механической работы.

5. Период колебаний математического маятника?

6. Виды деформаций. Закон Гука.

7. Закон изменения количества движения.

ЛАБОРАТОРНАЯ РАБОТА