Расчетная мощность. Номинальная мощность аккумуляторной батареи
Расчетная мощность. Номинальная мощность аккумуляторной батареи
Электромагнитный КПД, учитывающий влияние магнитных и механических потерь в электродвигателе для Р2 = 1,9 кВт hЭМ = 0,91 (рисунок 1).
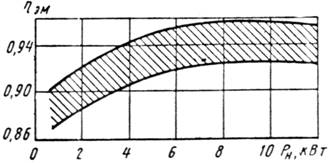
Рисунок 1 - Зависимость электромагнитного КПД стартерных электродвигателей от номинальной мощности
Расчетная электромагнитная мощность
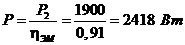 (1.1)
(1.1)
Кратность рабочей силы тока силе тока короткого замыкания в режиме номинальной мощности для двигателя с последовательным возбуждением k = 0,62 (рисунок 2).
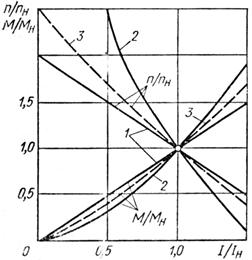
Рисунок 2 - Скоростные и моментные характеристики электродвигателей постоянного тока в относительных координатах:
1 - параллельное возбуждение;
2 - последовательное возбуждение;
3 - смешанное возбуждение
Падение напряжения на щетках принимаем постоянным и равным DUЩ = 1 В ([2], с. 39).
Расчетная ЭДС в обмотке якоря
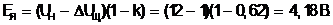 (1.2)
(1.2)
Сила тока в расчетном режиме работы
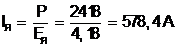 (1.3)
(1.3)
Суммарное сопротивление цепи якоря
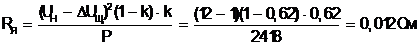 (1.4)
(1.4)
Максимальная электромагнитная мощность
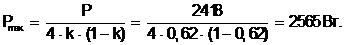 (1.5)
(1.5)
В режиме максимальной электромагнитной мощности (k = 0,5):
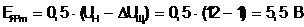 ; (1.6)
; (1.6)
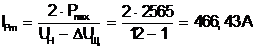 ; (1.7)
; (1.7)
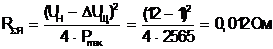 (1.8)
(1.8)
Номинальная емкость аккумуляторной батареи характеризуется величиной ее относительной энергии LОТН = (UH×C20)/Pmax [2, с. 68], зависимость которой от максимальной расчетной мощности оптимальных по массе электропусковых систем приведена на рисунке 3.
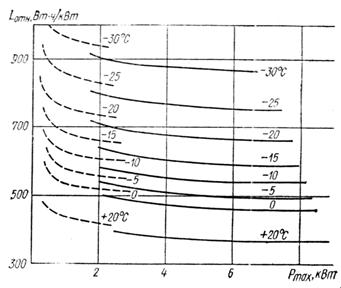
Рисунок 3 - Зависимость относительной энергии аккумуляторных батарей от максимальной расчетной электромагнитной мощности (пунктирные кривые при U=12 В)
Из рисунка 3 для Pmax = 2,565 кВт, и t = +25°C LОТН = 0,4 Вт×ч/Вт.
Номинальная емкость аккумуляторной батареи
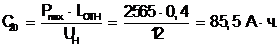 (1.9)
(1.9)
По полученному значению номинальной емкости выбираем аккумуляторную батарею 6СТ-90, С20 = 85,5 А×ч [3, с. 67].
Сопротивление аккумуляторной батареи принимаем равным
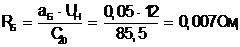 (1.10)
(1.10)
где аБ = 0,05 при С20 £ 100 А×ч.
Главные размеры электродвигателя
Соотношение мощности и частоты вращения
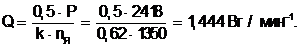 (2.1)
(2.1)
Диаметр якоря стартерных электродвигателей для оптимальных по массе электропусковых систем выбирается в зависимости от Q.
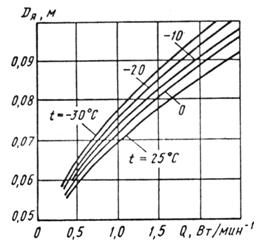
Рисунок 4 - Зависимости диаметра якоря стартерных электродвигателей от Q при различных температурах
Из рисунка 4 для Q = 1,444 Вт/мин-1 и t = +25°C находим DЯ = 0,077 м.
Диаметр корпуса
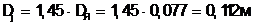 (2.2)
(2.2)
Начальные значения линейной нагрузки якоря А, индукции в воздушном зазоре Bd и коэффициента полюсного перекрытия ad находим соответственно из рисунка 5 для Dj = 0,112 м.
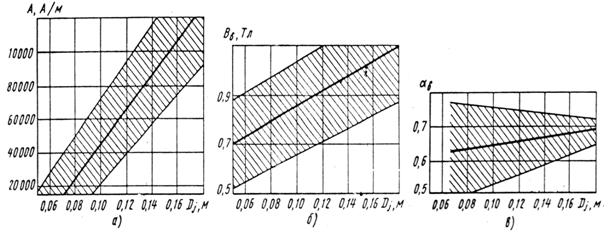
Рисунок 5 - Зависимость электромагнитных нагрузок стартерных электродвигателей от диаметра корпуса
Линейная нагрузка якоря (рисунок 5, а) A = 55000 А/м.
Расчетная индукция в воздушном зазоре (рисунок 5, б) Bd = 0,87 Тл.
Коэффициент полюсного перекрытия (рисунок 5, в) ad = 0,65.
Машинная постоянная
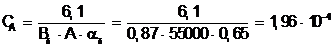 . (2.3)
. (2.3)
Длина пакета якоря
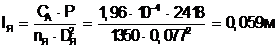 (2.4)
(2.4)
Полюсное деление
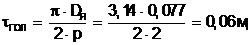 (2.5)
(2.5)
где p - число пар полюсов, для стартерных электродвигателей 2p=4.
Основной магнитный поток на два полюса
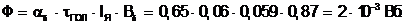 (2.6)
(2.6)
Обмотка якоря
Пакет якоря для уменьшения потерь на вихревые токи собирается из штампованных пластин листовой электротехнической стали толщиной примерно (1,...,1,2) мм. Для запрессовки пакета на валу якоря имеется продольная накатка [2, с. 50].
В стартерных электродвигателях широкое распространение получили волновые обмотки, которые имеют определенные преимущества перед петлевыми обмотками. В волновой обмотке проводники каждой параллельной ветви равномерно распределены под всеми полюсами, поэтому не требуются специальные уравнительные соединения (как в петлевой обмотке) для выравнивания ЭДС в параллельных ветвях, неравенство которых возникает из-за несимметрии магнитной системы машины.
Основным отличием волновой обмотки является то, что число параллельных ветвей не зависит от числа пар полюсов машины и всегда равно двум (2×аЯ = 2).
Число активных проводников обмотки якоря
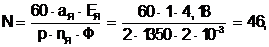 (3.1)
(3.1)
где аЯ = 1 - число пар параллельных ветвей обмотки якоря.
Число коллекторных пластин K равно числу секций обмотки якоря, а число секций волновой обмотки в стартерных электродвигателях равно числу пазов. Простая волновая обмотка может быть выполнена лишь при определенных соотношениях между числом секций и числом пар полюсов, т. е. результирующий шаг обмотки и шаг по коллектору
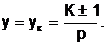 (3.2)
(3.2)
Так как результирующий шаг должен быть выражен целым числом, то простая волновая обмотка может быть выполнена только при нечетном числе пазов и коллекторных пластин, иначе возникают мертвые секции.
Число пазов ZПЗ в четырехполюсных стартерных электродвигателях должно быть нечетным (в пределах 19 … 31) [1, с. 75]. Принимаем ZПЗ = 23. Число витков в секции обмотки якоря
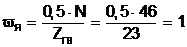 (3.3)
(3.3)
Соотношение длины пакета якоря и его диаметра
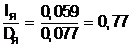
находится в рекомендованных [1, с. 75] пределах (0,75 … 1,25).
По формуле (3.2)
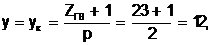
откуда первый частичный шаг, определяющий ширину секции по пазам y1 = 12, второй частичный шаг, определяющий расстояние между концом одной и началом следующей секции y2 = y - y1 = 12 - 6 = 6.
Падение напряжения в стартерной сети не должно превышать 2 В на 1000 А, т.е. сопротивление стартерных проводов и массы должно быть меньше 0,002 Ом [2, с. 39]. Принимаем RПР = 0,002 Ом.
Суммарное сопротивление обмотки якоря и последовательной обмотки возбуждения
RСТ = RSЯ - RБ - RПР = 0,012 - 0,007 - 0,002 = 0,003 Ом. (3.4)
Сопротивление обмотки якоря принимаем
RЯ = 0,6×RСТ = 0,59×0,003 = 0,00177 Ом. (3.5)
Средняя длина проводника
LЯ = lЯ + 1,2×tПОЛ = 0,059 + 1,2×0,06 = 0,131. (3.6)
Сечение проводников обмотки якоря
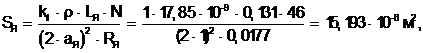 (3.7)
(3.7)
где kt - коэффициент, учитывающий изменение сопротивления обмотки якоря при изменении температуры. При первоначальном расчете температурный коэффициент можно принять равным единице;
r = 17,85×10-9 Ом×м - удельное сопротивление меди при t = 20°C.
По расчетной площади сечения для одновитковых секций выбираем прямоугольный провод с учетом отношения его толщины к ширине
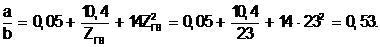
Расчетная ширина провода
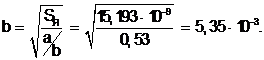 (3.8)
(3.8)
По расчетной площади сечения для одновитковых секций выбираем прямоугольный провод с учетом отношения его толщины к ширине
Выбираем прямоугольный провод толщиной a = 3,05×10-3 м, шириной b = 5,5×10-3 м и площадью сечения SЯ = 15,1×10-6 м2 [4, с. 563].
Отношение
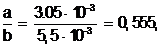
находится в допустимых [1, с. 76] пределах (0.33 … 0,73).
Сопротивление обмотки якоря
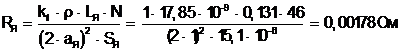 (3.10)
(3.10)
Отношение
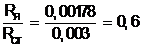
не выходит за рекомендуемые пределы (0,45 … 0,65).
Определение размеров паза
Форму и размеры паза выбираем из условия максимального его заполнения (для прямоугольного провода выбирают прямоугольный паз). Применяем полузакрытую форму паза, так как в открытых пазах затруднено крепление проводников обмотки якоря.
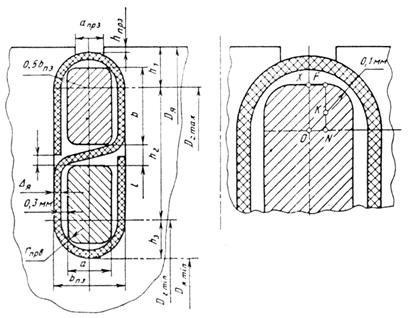
Рисунок 6 - Полузакрытый паз и его размеры с учетом технологических требований
Радиус закругления провода
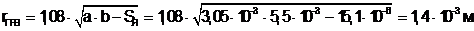 (4.1)
(4.1)
Ширина паза
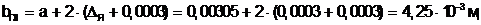 (4.2)
(4.2)
где DЯ = 0,0003 м - толщина изоляции паза.
Ширина прорези
aПРЗ = 0,6×a = 0,6×3,05×10-3 = 1,83×10-3. (4.3)
Максимальный диаметр второго участка зубцовой зоны
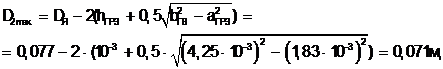 (4.4)
(4.4)
где hПРЗ= 10-3 м - высота прорези.
Высота зубца
hZ = h1 + h2 + h3 = 0,003 + 0,008 + 0,002 = 0,013 м. (5.6)
Зубцовые шаги по наружному диаметру якоря и в расчетных сечениях зубца:
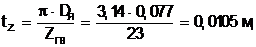 (5.7)
(5.7)
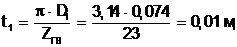 (5.8)
(5.8)
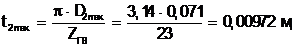 (5.9)
(5.9)
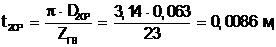 (5.10)
(5.10)
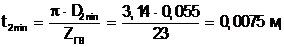 (5.11)
(5.11)
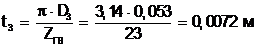 (5.12)
(5.12)
Ширина зубца в расчетных сечениях:
bZ = tz - aПРЗ = 0,0105 - 0,002 = 0,0085 м; (5.13)
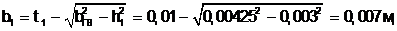 (5.14)
(5.14)
b2max = t2max - bПЗ = 0,00972 - 0,00425 = 0,00547 м; (5.15)
b2CP = t2CP - bПЗ = 0,0086 - 0,00425 = 0,00435 м; (5.16)
b2min = t2min - bПЗ = 0,0075 - 0,00425 = 0,00325 м; (5.17)
b3 = t3 - 0,866×bПЗ = 0,0072 - 0,866×0,00425 = 0,00352 м. (5.18)
Коэффициент заполнения пакета статора сталью принимаем kСТЛ = 0,95.
Магнитные индукции в расчетных сечениях зубца:
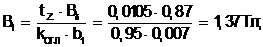 (5.19)
(5.19)
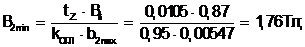 (5.20)
(5.20)
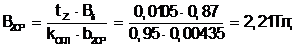 (5.21)
(5.21)
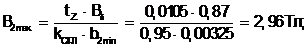 (5.22)
(5.22)
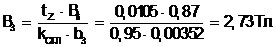 (5.23)
(5.23)
Значение индукции B2max = 2,96 Тл не выходит за рекомендуемые [1, с. 76] пределы 1,8 … 3,0 Тл.
Зубцовые коэффициенты для расчетных сечений зубца:
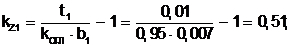 (5.24)
(5.24)
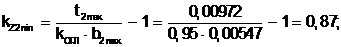 (5.25)
(5.25)
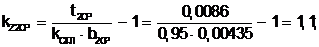 (5.26)
(5.26)
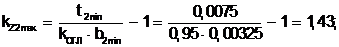 (5.27)
(5.27)
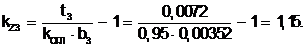 (5.28)
(5.28)
Напряженность магнитного поля определяем по зависимостям, приведенным на рисунке 9.
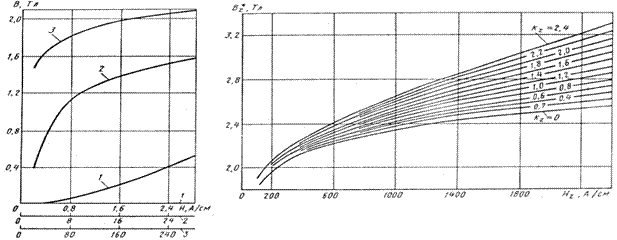
Рисунок 9 - Зависимости B = f(H) при различных зубцовых коэффициентах
Для B1 = 1,37 Тл H1 = 1530 А/м.
Для B2min = 1,76 Тл H2min = 6500 А/м.
Для B2CP = 2,21 Тл и kz2cp = 1,1 H2min = 42000 А/м.
Для B2max = 2,96 Тл и kz2max = 1,43 H2max = 235000 А/м.
Для B3 = 2,73 Тл и kz3 = 1,15 H3 = 165000 А/м.
Средняя напряженность на втором участке
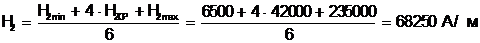 (5.29)
(5.29)
МДС для первого участка
F1 = 2×h1×H1 = 2×0,003×1530 = 10 А. (5.30)
МДС для второго участка
F2 = 2×h2×H2 = 2×0,008125×68250 = 1110 А. (5.31)
МДС для третьего участка
F3 = 2×h3×H3 = 2×0,002125×165000 = 700 А. (5.32)
МДС для зубцовой зоны
FZ = F1 + F2 + F3 = 9 + 1110 + 700 = 1720 А. (5.33)
Принимаем длину воздушного зазора d = 0,0007 м. Коэффициент воздушного зазора
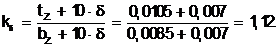 (5.34)
(5.34)
МДС для воздушного зазора
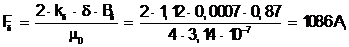 (5.35)
(5.35)
где m0 = 4×p×10-7 Гн/м - абсолютная магнитная проницаемость воздуха.
Длина корпуса
lj = 1,7×lЯ = 1,7×0,059 = 0,1 м. (5.36)
Коэффициент рассеивания магнитного потока ks = 1,15.
Площадь расчетного сечения при Bj = 1,3 Тл
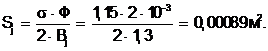 (5.37)
(5.37)
Толщина расчетного сечения
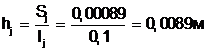 (5.38)
(5.38)
Диаметр расточки полюсов
Di = DЯ + 2×d = 0,077 + 2×0,0007 = 0,00784 м. (5.39)
Длина полюсной дуги
bi = ad×tПОЛ + 2×d = 0,65×0,06 + 2×0,0007 = 0,04 м. (5.40)
Длина наконечника
lHK = 0,5×(bi - bm) = 0,5×(0,04 - 0,027) = 0,0065 м. (5.47)
Диаметр вала якоря
DB = 0,3×DЯ = 0,3×0,077 = 0,023 м. (5.48)
Высота сердечника якоря
hЯ = 0,5×(DЯ - DВ - 2×hZ) = 0,5×(0,077 - 0,023 - 2×0,013) = 0,014 м. (5.49)
Магнитная индукция в сердечнике:
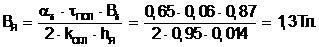 (5.50)
(5.50)
Магнитная индукция в полюсе:
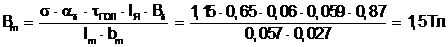 (5.51)
(5.51)
Магнитная индукция в корпусе:
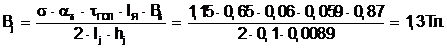 (5.52)
(5.52)
Магнитные индукции BЯ, BМ, Вj в расчетном режиме не выходят за рекомендуемые пределы 1,0 … 1,7 Тл [1, с. 76].
Сопротивление катушки
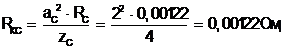 (6.4)
(6.4)
где zC = 4 - число катушек.
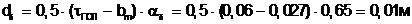 (6.5)
(6.5)
Максимально возможная ширина катушки
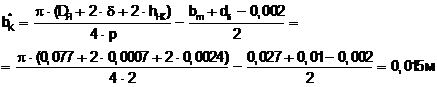 (6.6)
(6.6)
Средняя длина витка катушки
LK = 2×lm + 2×bm + p×b*K = 2×0,057 + 2×0,027 + p×0,015 = 0,215 м. (6.7)
Площадь сечения провода
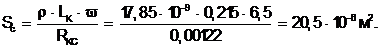 (6.8)
(6.8)
Высота катушки
hK = hm - hHK = 0,008 - 0,0024 = 0,0056 м. (6.9)
Витки катушек изолированы электроизоляционным картоном толщиной DИЗ = 0,4×10-3 м. Снаружи катушки изолированы хлопчатобумажной лентой толщиной 0,25 мм и шириной 15 мм, пропитанной лаком. После пропитки и сушки толщина внешней изоляции катушки составляет DВН = 10-3 м [2, с. 49].
Ширина провода
bC = hK - DВН = 0,0056 - 0,001 = 0,0046 м. (6.10)
По рассчитанному значению площади сечения выбираем провод шириной bC = 0,0108 м, толщиной аC = 0,00181 м и площадью сечения SC = 19,3×10=6 м2 [4, с. 562].
Действительная ширина катушки
bK = ac×v + DИЗ×(v-1) + 2×DВН = 0,00181×6,5 + 0,4×10-3×5,5 + 2×10-3 = 0,015 м. (6.11)
Уточненное значение сопротивления катушки
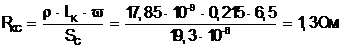 (6.12)
(6.12)
Уточненное значение сопротивления обмотки
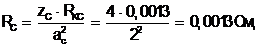 (6.13)
(6.13)
Плотность тока в обмотке возбуждения
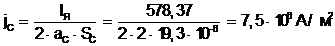 (6.14)
(6.14)
меньше допустимого ([1], с. 76) значения 30×106 А/м2.
Рабочие характеристики
Сила тока в режиме торможения
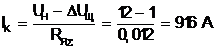 (7.1)
(7.1)
Сила тока в режиме максимальной электромагнитной мощности
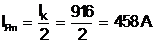 (7.2)
(7.2)
Максимальная электромагнитная мощность
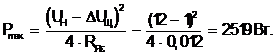 (7.3)
(7.3)
Параметры, необходимые для построения рабочих характеристик, определяем для нескольких значений силы тока стартера. Ниже приведены результаты расчета для силы тока IЯm = 458 А.
Напряжение на выводах стартера
UCT = UH - RСТ×IЯ = 12 - 0,003×458 = 10,6 В. (7.4)
Полезная мощность
P2 = P - DPМ = 2519 -309 = 2210 Вт (7.26)
Схема управления стартером
В качестве схемы управления применяем схему с однообмоточным тяговым реле, питание на обмотку которого поступает непосредственно через контакты S выключателя зажигания при повороте ключа в положение «Стартер». Якорь реле втягивается в электромагнит, через рычажный механизм вводит шестерню в зацепление с венцом маховика и в конце хода замыкает силовые контакты К в цепи питания электродвигателя М. Электродвигатель начинает вращаться и проворачивать коленчатый вал ДВС.
После пуска ДВС шестерня от вала стартера отсоединяется обгонной муфтой, а при переводе ключа в положение «Зажигание» якорь отключенного от источника питания тягового реле и приводной механизм под действием пружины возвращаются в исходной положение.
Электрическая схема управления электростартером приведена на рисунке 18.
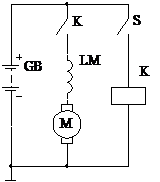 |
Рисунок 18- Электрическая схема управления электростартером.
Приложение 1 - Кривая намагничивания
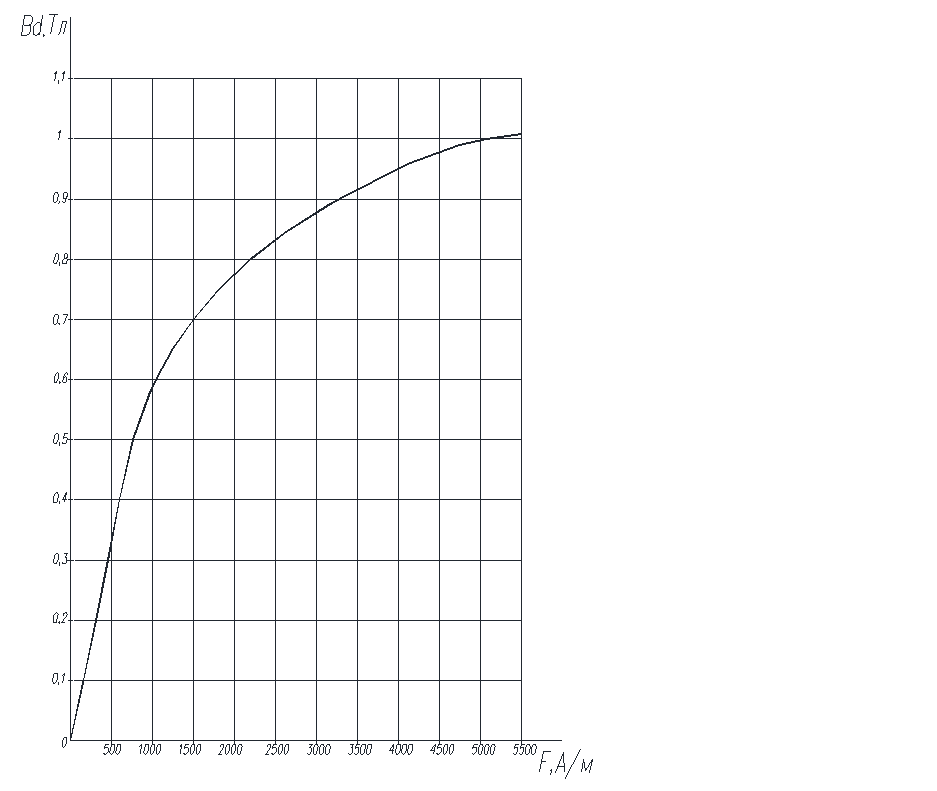
Рисунок 1 - Кривая намагничивания
Приложение 2 - Рабочие характеристики
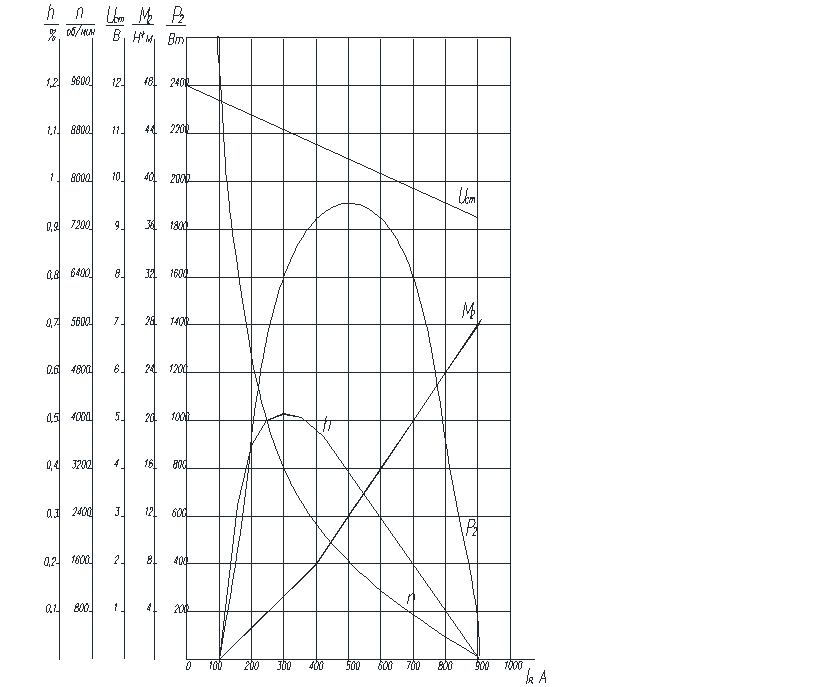
Рисунок 1 - Рабочие характеристики
Приложение 3 - Зависимость числа оборотов от температуры
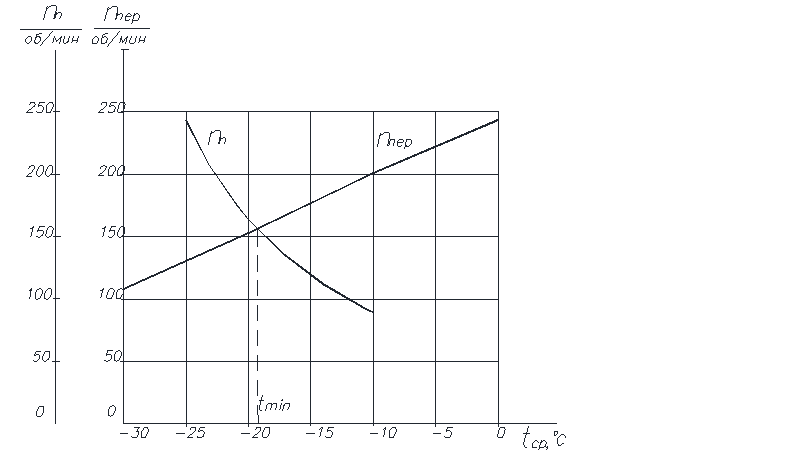 Рисунок 1 - Зависимость числа оборотов от температуры
Рисунок 1 - Зависимость числа оборотов от температуры
Список литературы
1. Теория, конструкция и расчет автотракторного электрооборудования. Учебник для машиностроительных техникумов по специальности "Автотракторное электрооборудование"/Л. В. Копылова, В. И. Коротков, В. Е. Красильников; Под ред. М. Н. Фесенко и др. - М. Машиностроение, 1992. - 384 с., ил.
2. Теория, конструкция и расчет автотракторного электрооборудования. Учебник для машиностроительных техникумов по специальности "Автотракторное электрооборудование"/Л. В. Копылова, В. И. Коротков, В. Е. Красильников; Под ред. М. Н. Фесенко и др. - М. Машиностроение, 1979. - 344 с., ил.
3. Электрическое и электронное оборудование автомобилей/ С.В.Акимов, Ю.И.Боровских, Ю.П.Чижков. - М.: Машиностроение, 1988. - 280 с.: ил.
4. Сергеев П.С. Проектирование электрических машин. Изд. 3-е переработ. - М.: Энергия,1969. - 632 с.
5. Ютт В.Е. Электрооборудование автомобилей: Учеб. для студентов вузов. - 3-е изд., перераб. и доп. - М.: Транспорт, 2000. 320 с.
6. Чижков Ю.П., Акимов С.В. Электрооборудование автомобилей. Учебник для ВУЗов. - М.: Издательство «За рулем», 1999. - 384 с., ил.
Стандарт предприятия. Общие требования к оформлению пояснительных записок и чертежей. СТП-1-У-НГТУ-98. / НГТУ, Нижний Новгород, 1998 г
Расчетная мощность. Номинальная мощность аккумуляторной батареи
Электромагнитный КПД, учитывающий влияние магнитных и механических потерь в электродвигателе для Р2 = 1,9 кВт hЭМ = 0,91 (рисунок 1).

Рисунок 1 - Зависимость электромагнитного КПД стартерных электродвигателей от номинальной мощности
Расчетная электромагнитная мощность
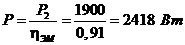 (1.1)
(1.1)
Кратность рабочей силы тока силе тока короткого замыкания в режиме номинальной мощности для двигателя с последовательным возбуждением k = 0,62 (рисунок 2).

Рисунок 2 - Скоростные и моментные характеристики электродвигателей постоянного тока в относительных координатах:
1 - параллельное возбуждение;
2 - последовательное возбуждение;
3 - смешанное возбуждение
Падение напряжения на щетках принимаем постоянным и равным DUЩ = 1 В ([2], с. 39).
Расчетная ЭДС в обмотке якоря
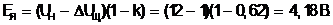 (1.2)
(1.2)
Сила тока в расчетном режиме работы
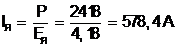 (1.3)
(1.3)
Суммарное сопротивление цепи якоря
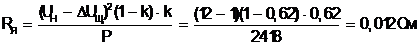 (1.4)
(1.4)
Максимальная электромагнитная мощность
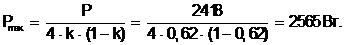 (1.5)
(1.5)
В режиме максимальной электромагнитной мощности (k = 0,5):
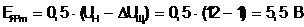 ; (1.6)
; (1.6)
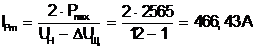 ; (1.7)
; (1.7)
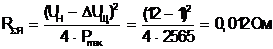 (1.8)
(1.8)
Номинальная емкость аккумуляторной батареи характеризуется величиной ее относительной энергии LОТН = (UH×C20)/Pmax [2, с. 68], зависимость которой от максимальной расчетной мощности оптимальных по массе электропусковых систем приведена на рисунке 3.

Рисунок 3 - Зависимость относительной энергии аккумуляторных батарей от максимальной расчетной электромагнитной мощности (пунктирные кривые при U=12 В)
Из рисунка 3 для Pmax = 2,565 кВт, и t = +25°C LОТН = 0,4 Вт×ч/Вт.
Номинальная емкость аккумуляторной батареи
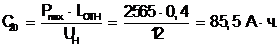 (1.9)
(1.9)
По полученному значению номинальной емкости выбираем аккумуляторную батарею 6СТ-90, С20 = 85,5 А×ч [3, с. 67].
Сопротивление аккумуляторной батареи принимаем равным
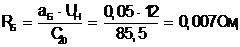 (1.10)
(1.10)
где аБ = 0,05 при С20 £ 100 А×ч.
