Сравнение дроссель-эффекта с температурным эффектом адиабатного расширения

Из курса общей термодинамики (раздел «Вычисление энтропии») известно соотношение:

.

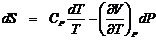Для обратимого адиабатного процесса (dS = 0) это уравнение приобретает следующий вид:

,

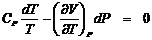откуда следует

.

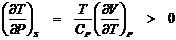Обозначим температурный эффект обратимого адиабатного расширения как .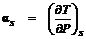

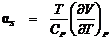. (10.1)

Сравним α_S с дроссель-эффектом α_i (примечание: α_i иногда называют температурным эффектом необратимого адиабатного процесса расширения).

.

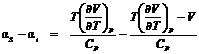Окончательно

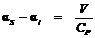. (10.2)

Из уравнения (10.2) следует, что при адиабатном расширении газ охлаждается сильнее, чем при адиабатном дросселировании.

Для получения низких температур, например, сжижение газов, целесообразно использовать детандеры – расширительные цилиндры, в которых производится адиабатное расширение газа.

Как было показано выше, охлаждение рабочего тела при дросселировании (α_i > 0), возможно лишь при расположении начальных точек дросселирования (Р₁, Т₁) в определенных областях,

Так, например, при Т₁> Т_{ИНВ max} охлаждение газа при дросселировании невозможно ни при каких значениях начального давления Р₁.

В случае адиабатного расширения охлаждение рабочего тела (даже идеального газа) достигается всегда, при любом сочетании начальных значений термодинамических параметров (Р₁, Т₁) .

Последнее является большим достоинством метода охлаждения за счет адиабатного расширения. Недостатком этого метода является техническая сложность осуществления регулирования температуры охлаждения. Метод дросселирования свободен от этого недостатка, но приводит к некоторому снижению эффективности работы холодильной установки.

Как следует из уравнения (10.2), в области двухфазных состояний вещества, где С_Р → ∞, α_S = α_i, т.е. одинаковый перепад давления Р₁ – Р₂, приводит к одинаковому понижению температуры Т₁ – Т₂. Чем больше реальный процесс адиабатного расширения газа в детандере отличается от обратимого действием сил трения, ведущих к нагреванию газа, тем сильнее α_S стремится к α_i.

Процесс дросселирования из-за его необратимости приводит к снижению работоспособности газа (пара) по сравнению с адиабатным обратимым расширением. Рассмотрим два варианта расширения пара от P₁ до P₃:

1. адиабатное обратимое расширение, при котором теоретическая работа пара равна разности i₁ – i₃;
2. дросселирование пара от Р₁ до Р₂ (Р₂ > Р₃) с последующим адиабатным расширением пара от Р₂ до Р₃.

Теоретическая работа пара при таком варианте расширения будет меньше и равна разности i₂ – i₄, где i₂ = i₁, а i₄ > i₃. Это иллюстрируется рис. 10.1

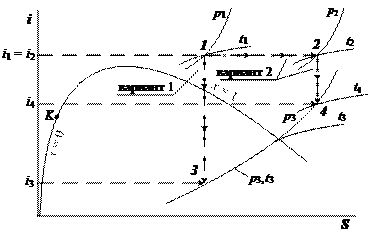
Рис. 10.1. Влияние процесса дросселирования на работоспособность пара

Потеря работоспособности 1 кг пара в приведенном примере составит:

.

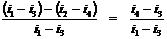Приложение

П.1. Вывод формулы для дифференциального дроссель-эффекта (вариант автора пособия)

. (П1.1)

а) Определим для формулы (П1.1). Пусть i = i(T, V),

тогда

,

откуда

. (П1.2)

б) Определим . Пусть i = i(Р, V),

тогда

,

откуда

. (П1.3)

в) После подстановки (П1.2) и (П1.3) в уравнение (П1.1) имеем:

,

. (П1.4)

г) Определим . Так как i = U + PV, то di =dU + PdV + VdP,

откуда:

. (П1.5)

Определим . Так как dU = ТdS – PdV,

то:

.

По третьему типу дифференциальных соотношений термодинамики

.

Тогда

. (П1.6)

Подставим (П1.6) в уравнение (П1.5):

,

. (П1.7)

д) Определим для формулы (П1.4). Представим эту производную в виде произведения двух частных производных:

.

Из общей термодинамики известно, что = С_Р.

Тогда

. (П1.8)

Общая формула для теплоемкостей однородных систем, как известно из общей термодинамик, имеет вид:

.

Для изобарного процесса из этой формулы следует:

. (П1.9)

Подставим (П1.9) в (П1.8):

и

. (П1.10)

е) Подставим П(1.10) и (П1.7) в формулу (П1.4):

.

Выразим произведение в знаменателе через произведение других частных производных, используя дифференциальные соотношения термодинамики:

. (П1.11)

Тогда окончательно

. (П1.12)

П.2. Вывод формулы для инверсионной кривой (вариант автора пособия)

Продифференцируем уравнение (8.1):

.

Но удельный объем V является функцией Р и Т, поэтому

.

В соответствии с правилом нахождения полного дифференциала функции двух переменных запишем:

,

,

,

и окончательно

. (П2.1)

П.3. Вывод приближенной формулы для дифференциального дроссель-эффекта (вариант автора пособия)

Формулу (9.11) можно представить в другом виде, если подставить туда значение Р из уравнения (9.9):

.

Умножив числитель и знаменатель на (V – b), получим:

. (П3.1)

Подставим (П3.1) в формулу (4.4):

.

Окончательно

. (П3.2)

Как показывает численный анализ, при V >> b, слагаемыми, содержащими в знаменателе уравнения (П3.2) V во второй степени и выше, можно пренебречь.

Тогда:

и окончательно:

. (П3.3)

Список литературы

1. Тепломеханика / В. Н. Луканин, М. Г. Шатров, Г. М. Камфер и др.; Под ред. В.Н. Луканина. – М. : Высшая школа, 1999. – 671 с.

2. Вукалович, М. П. Термодинамика / М. П. Вукалович, И. И. Новиков. – М. : Машиностроение, 1972. – 672 с.

3. Зубарев, В.Н. Практикум по технической термодинамике /В. Н. Зубарев, А. А. Александров, В. С. Охотин. – М.: Энергоатомиздат, 1986. – 304 с.

Содержание

Предисловие. 3

1. Общие сведения о дросселировании. 3

2. Дросселирование идеального газа. 7

3. Дросселирование пара. 8

4. Дроссель-эффект Джоуля-Томсона. 9

4.1. Молекулярно-кинетическая природа изменения температуры газа в процессе дросселирования 10

4.2. Общие формулы для дифференциального дроссель-эффекта. 12

5. Дифференциальный дроссель-эффект в области двухфазных состояний вещества 15

6. Дифференциальный дроссель-эффект в критической точке. 18

7. Дифференциальный дроссель-эффект в однофазных областях. Точки инверсии. 19

8. Инверсионная кривая. 22

9. Дросселирование рабочего тела, подчиняющегося уравнению Ван-дер-Ваальса 25

9.1. Основные сведения об уравнении Ван-дер-Ваальса. 25

9.2. Качественный анализ процесса дросселирования с помощью уравнения Ван-дер-Ваальса 29

9.2.1. Построение инверсионной кривой. 29

9.3. Расчетное определение термодинамических параметров в точке максимума инверсионной кривой 33

9.4. Расчетное определение максимальной и минимальной температуры инверсии 36

10. Сравнение дроссель-эффекта с температурным эффектом адиабатного расширения 39

Приложение. 42

П.1. Вывод формулы для дифференциального дроссель-эффекта (вариант автора пособия) 42

П.2. Вывод формулы для инверсионной кривой (вариант автора пособия) 45

П.3. Вывод приближенной формулы для дифференциального дроссель-эффекта (вариант автора пособия) 46

Список литературы.. 49

Учебное издание

Составители:

Диденко Валерий Николаевич

В редакции составителя

Подписано в печать . Формат 60×84/16. Усл. печ. л.

Тираж ____ экз. Заказ №___

Отпечатано в типографии Издательства ИжГТУ

Издательство и типография Ижевского государственного

технического университета. 426069, Ижевск, ул. Студенческая, 7