Внутренняя энергия. Опыты Джоуля.

Глава 1.

Первый закон термодинамики.

Введение

Количественные характеристики: температура, работа, внутренняя энергия и теплота.

Обсуждается научное понятие температуры.

Принцип, на котором основывается определение температуры найден после установления I и II законов термодинамики и поэтому называется нулевым законом.

I закон выражает идею сохранения энергии, которая сначала возникла в механике, потом распространилась на электростатику и электродинамику.

Опыты Джоуля в 1840-1845 показали, что можно включить теплоту в закон сохранения энергии.

I закон вводит понятие внутренней энергии.

1. Система, окружающая среда, состояние системы и параметры состояния.

Термодинамическая система– это рассматриваемая часть материальной вселенной. Она отделена от окружающей среды замкнутой поверхностью – границей.

Система называется изолированной, если эта граница исключает любые взаимодействия с окружающей средой.

Система называется открытой, если через границу переходит вещество, и система называется закрытой, если нет. При этом теплота может поступать в закрытую систему или выделяться из неё.

Система может претерпеть изменения, переходя от начального состояния к конечному, при которых она обменивается теплотой и работой с окружающей средой; при этом изменяется как система, так и окружающая среда. Если граница не пропускает теплоту, то любой процесс, происходящий в системе называется адиабатическим, а границу – адиабатической оболочкой.

Если при данных условиях система является равновесной, то говорят, что она находится в некотором определенном состоянии, то есть каждое из ее свойств имеет конкретное численное значение.

Установлено, что для данного количества газа или жидкости. Состояние полностью определяется двумя переменными из трех: p, V, T. Эти переменные называются параметрами состояния.

Термодинамика имеет дело с переходами от некоторого начального состояния к некоторому конечному. При этом переходе может происходить теплообмен и совершаться работа над системой или окружающей средой.

1.2 Нулевой закон термодинамики. Температурная шкала.

Для определения понятия температуры нужно ввести понятие теплового равновесия.

Приводим в тепловой контакт две закрытые системы. Свойства обоих систем будут изменяться до такого состояния, когда дальнейшие изменения ужу не происходят. Это и есть состояние теплового равновесия.

Чтобы установить, находятся ли две системы при одной и той же температуре, надо привести системы в соприкосновение и посмотреть, изменяются ли их свойства.

Отсутствие изменений свидетельствует о том, что системы находятся при одинаковой T.

Нулевой закон.

Рассмотрим 3 системы: A, B, C.

Экспериментально установим, что если тело A и тело B находится в тепловом равновесии с телом C, то A и B находятся в тепловом равновесии друг с другом. Этот экспериментальный факт называется нулевым законом термодинамики.

Другая формулировка нулевого закона термодинамики:

Если две системы находятся в тепловом равновесии друг с другом, то их температуры одинаковы, если не находятся в тепловом равновесии - то их температуры различны.

Температурная шкала.

Пусть тело B находится в состоянии, характеризующимся (V_B и P_B) B óA (V_A и P_A), P_a,V_a – переменные, но ó сохраняется.

Пусть тело A (газ, жидкость) находятся в равновесии с B, P_a и V_a определяются из опыта.

Существует много сочетаний P_a и V_a , соответствующих равновесию. Эти пары значений образуют график зависимости P_a от V_a. Полученная кривая называется изотермой и согласно нулевому закону не зависит от природы тела B. Так как заменив тело B любым иным телом, находящимся в равновесии с B, мы получим тот же результат.

Изменив тепловое состояние B и повторив опыт мы получим другую изотерму для A.

Каждой найденной изотерме можно приписать некоторую 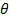температуру и таким образом построить температурную шкалу.

Тела с одинаковой 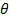сохранят неизменными все свойства, если их привести в тепловой контакт друг с другом через поверхность раздела, которая позволяет им иметь любые давления и любой химический состав.

Существует много температурных шкал, но самая полезная основана на поведении идеальных газов. Оно получено экстраполяцией поведения реальных газов с нулевым давлением к нулевому давлению. Температурная шкала идеального газа тождественна той шкале, которую дает статистическая механика.

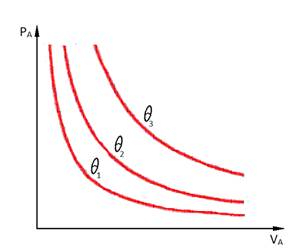
Изотермы для вещества A. Для другого вещества это график может выглядеть иначе.

Пары переменных P и V, составляющие одной и той же T м. б. представлены в виде некоторой функции (например кривые на рисунке 1.1)

f(P,V)=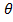

(1.1)

Уравнения такого типа называются уравнениями состояния для газа или жидкости .

У любого реального газа (жидкости) свое уравнение состояния.

Из (1.1) следует, что существует функция состояния вещества называемая температурой, которая имеет одинаковое значение для тел, находящихся в тепловом равновесии друг с другом.

Используем наши знания о поведении газов при низких P (например, закон Бойля).

По мере понижения P данного количества газа он всё точнее подчиняется уравнению

PV=k (T const)

(1.2)

А произведение PV (газов) экстраполированное к нулевому давлению ~ число n молей газа к функции температуры 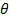=T

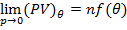
(1.3)

Пусть 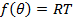, где R - газовая постоянная, T – температура идеального газа

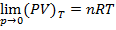
(1.3')

(Для идеального газа PV=nRT)

Чтобы теперь построить температурную шкалу требуется определить значение T какого-нибудь стандартного состояния, чтобы можно было вычислить газовую постоянную R.

Напоминание

Единица измерения т.д. T – градус K в системе СИ установлена следующим образом: отсчет по шкале начинается от абсолютного нуля, а T=273,1600 приписывается тройной точке воды (лед, жидкость и пар находятся в равновесии в отсутствии воздуха)

T плавления льда (T, при которой лед и вода в равновесии в присутствии воздуха при Р=1 атм.) дает «0» на шкале С.

Этой точке приписана Т на 0.0100⁰С ниже Т тройной точки воды, то есть 273, 1500К.

Т.о. т.д.Т связана с t по C: t=T-273,1500.

Универсальная газовая постоянная R.

Тщательные эксперименты с молекулярным кислородом показывают, что при P ->0. Произведение PV для 1моля кислорода (31, 9988)-> 22,41383 л*атм при 0⁰ С (273,1500К)

Можно вычислить R и посредством (1.3)

Надо вспомнить систему СИ:

Стандартная атмосфера равна давлению ртутного столба h=76см при 0⁰С в точке Земли, где g=9,80665м/с², ρ_Hg=13,5951г/см³

Тогда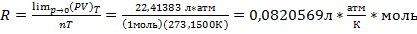

В системе СИ ед. [P]=Па=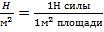

Давление одной стандартной атмосферы в Па можно вычислить

P=(0,76см)(13,5951*10³ кг/м³)(9,80665м/с²)=101325 Па=101325Н/м²

P - давление есть сила, приходящаяся на 1 единицу площади.

Размерности:

[P*V]=[F*l]=[w]=[E]

R можно выразить в [Дж]

R=PV/nT=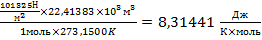

Удобно пользоваться законом идеальных газов в расчете на 1 моль газа

PV=RT, где V с «чертой»

(1.4)

V - объем, приходящийся на 1 моль газа.

Работа. Внутренняя энергия

1.3.1 Работа

В т.д-ке теплота и работа – алгебраические величины, они м.б. >0 и <0, сила – векторная величина.

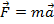
Сила которая сообщает массе m ускорение .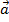

Работа ( 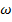) – скалярная величина.

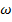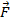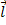=( , ) – скалярное произведение.

l – длина пути.

[w]=1Дж=Н*м

Бесконечно малое количество работы, совершенное силой f на пути dl:

fdl=PAdl=PdV,

(1.5)

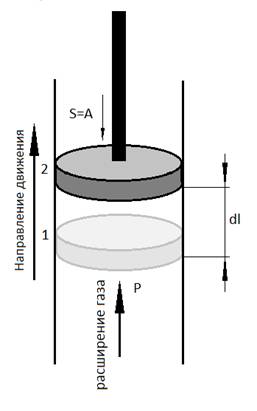
т.о. бесконечно малое количество работы, производимое расширяющимся газом, которое сдвигает поршень на dl=PdV.

Работа – величина алгебраическая. Пусть 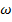>0, когда внешняя сила совершает работу над системой, 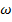<0 показывает, что над системой совершает работу над окружающей средой. (пример – см. рис. При расширении газа, давящего на поршень)

Теплота

Данное изменение состояния системы м.б. произведено не только из 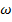в адиабатических условиях, но и другим способом. В опыте Джоуля: эквивалентное изменение можно получить, погружая нагретое тело в воду в калориметре. При этом теплота переходит от теплового источника (нагретое тело) к воде. В результате этого опыта повышается T воды и ее внутренняя энергия U.

В опытах, подобным опытам Джоуля, найдено что затрата 4.184Дж работы производит такое же изменение состояния, как и 1 кал теплоты, полученный системой извне.

Напомним, что изменение состояния сопровождается изменением свойств: T; P; V;

Теплота – алгебраическая величина; пусть q>0, когда закрытая система поглощает теплоту из окружающей среды; и q<0 показывает, что система отдает q окружающей среде.

Если переход теплоты q к системе не сопровождается никакой работой, то вызванное этим переходом изменение внутренней энергии U:

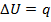(работа не совершается в закрытой системе)

(1.7)

Т.о. теплота, поглощенная закрытой системой в процессе при котором совершается работа, равна приросту внутренней энергии.

Первый закон термодинамики

Пусть закрытая система переходит из состояния 1 в состояние 2, при этом сама система совершает работу (или над ней совершается работа) и приведенная в контакт с тепловым источником система приобретает или теряет теплоту. Применим (1.6) (адиабатические условия) к системе и тепловому источнику.

Изменение и прирост = совершенной над системой работе.

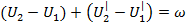
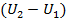– Изменение внутренней энергии системы.

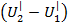- Изменение внутренней энергии теплового источника.

Теплота q, сообщенная системе (равная убыли внутренней энергии источника) равна теплоте с обратным знаком, полученной тепловым источником (нагретое тело) и согласно (10) усл. 1.7: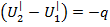

Окончательно I закон термодинамики выражается:

1-я часть I закон термодинамики:

+

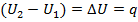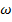
(1.8)

2-я часть I закон термодинамики:

Содержит утверждение, что термодинамическая q, определяемая этим уравнением, является функцией только состояния системы.

Важно!

I закон термодинамики позволяет определить только изменение внутренней энергии, но не ее абсолютную величину.

Если U=const, то совершенная 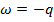поглощает.

Если U<0, то система теряет энергию, и эта энергия выделяется в виде теплоты и работы совершенной системой самой.

Другая формулировка:

Энергию можно превратить из одной формы в другую, но нельзя создать или уничтожить и общее количество энергии в изолированной системе постоянно.

( О соотношении Эйнштейна )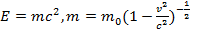

Обратимые процессы

Обратимым называется процесс, который можно в любой момент заставить протекать в обратном направлении, изменив какую-нибудь независимую переменную на бесконечно малую величину.

Обратимый процесс часто определяют как ряд последовательных состояний равновесия. Такое представление часто используют как идеализацию реальных процессов.

Обратимые процессы очень важны для теории, потому что они дают наибольшую работу, которая может быть вообще получена при данном изменении от состояния 1 до состояния 2. Это как раз то количество работы, которое необходимо, чтобы вернуть систему в исходное состояние.

При необратимом процессе работы производится меньше, чем нужно затратить, чтобы вернуть систему в начальное состояние.

Пример:

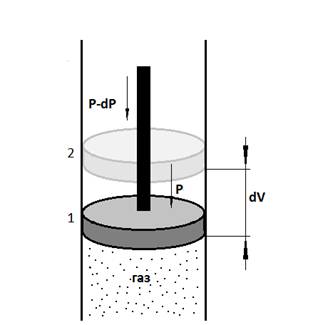
При таком расширении газа в цилиндре давление его уменьшается пока не станет равным внешнему давлению, после этого поршень перестает двигаться. Следующее бесконечно малое уменьшение давления вызывает новое расширение газа на dV. Т.о. происходит ряд последовательных приращений V.

Во время любой отдельной стадии расширения давление в газе постоянно (с точностью до dP – бесконечно малое)

Работа, производимая на любой стадии, равна внешнему давлению, x на «-dV».

Общее количество работы, которое можно получить при обратимом расширении газа от начального V₁ до конечного V₂ и равно:

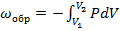на любой стадии

(1.12)

Поскольку на любой стадии расширения газ находится при равновесном давлении (с точностью до dP) можно подставить в формулу выражение для зависимости давления от V, полученное из равновесных данных равенство.

Если бы газ расширялся быстро, такую подстановку уже нельзя было бы сделать.

Только в том случае, когда расширение проводится обратимо при T=const, получается достаточное количество энергии, чтобы осуществить обратный процесс сжатия газа до исходного состояния.

Пример:

Вывести формулу для максимальной работы, получаемой при изотермическом расширении идеального газа в обратимом процессе.

T=const; P=nRT/V, подставим в (1.12)

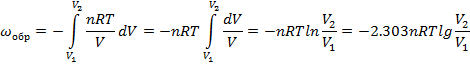
Если количество газа составляет 1 моль, то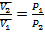

Тогда

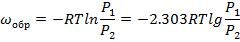
Численный пример:

Какова работа, производимая при обратимом расширении 1 моля идеального газа при 0⁰С от 2.24 до 22.4л?

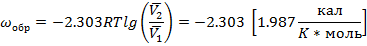
(273.15K)lg=-1250 кал/моль=-2.303[8.314Дж/(К*моль)]

(273.15К)lg10=-5230Дж/моль

Другой пример обратимого процесса – испарение жидкости при изменении T на бесконечно малую величину на каждой стадии процесса в следующей схеме эксперимента:

Жидкость в цилиндре снабженном поршнем, вся система находится в равновесии при T_{резервуара}=Т_р1

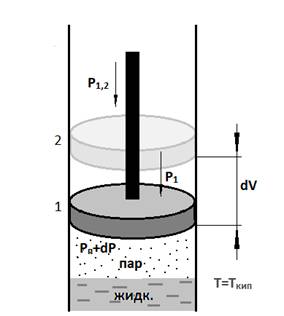
Пусть Т_р1+dT ->P+dP -> поршень поднимается; V увеличивается, следовательно давление падает, испаряется дополнительное количество жидкости. Как только давление пара над жидкостью станетравным внешнему давлению поршень остановится.

Давление таким образом поддерживается постоянным. Теплота, за счет которой происходит испарение иподдерживается T=const, поступает из теплового резервуара.

Этот процесс поглощения теплоты и совершения внешней работы обратим, поскольку в любой момент испарение можно приостановить, понизив Т на бесконечно малую величину или повысив P_{внешнее} на бесконечно малую величину так, чтобы P_внутр.=P_внеш.

Если еще увеличить P_внеш. На бесконечно малую величину, то пар начнет конденсироваться, при этом в тепловой резервуар будет возвращаться теплота, поглощенная при испарении.

[Задача 4? ]

Теплоёмкость

Определение:

Теплоёмкостью называется количество теплоты, необходимое для того, чтобы повысить Т системы на какую-то определенную величину (обычно на 1⁰), т.е. отношение поглощенной теплоты к приросту T: q/ T

Теплоёмкость при данной Т представляет собой предел к которому стремится это отношение при уменьшении T.

C=

Пусть существует система химически инертная, обладает постоянной массой m и совершает работу расширения.

U=f(T,V) U – функция состояния

Полный дифференциал U:

(1.15)

– изменение внутренней энергии за счет изменения Т

- изменение внутренней энергии за счет изменения V

Поскольку система сама совершает работу (расширение), то

и =>

(1.16)

Т.о. количество поглощенной теплоты зависит не только от прироста T, но и от изменения V.

Пусть V=const: или

(1.17)

- измеряется экспериментально при постоянном объёме.

С другой стороны в такой же системе H – функция(P,T) и

(1.18)

(1.19)

Как соотносятся C_p и C_v?

C_p> C_v, так как нагревание вещества при P=const всегда сопровождается работой расширения.

Поделим 1.16 на dT:

Пусть P=const:

(1.20)

Для одного моля чистого вещества:

(1.21)

{ -мольные C}

Велbчину можно измерить экспериментально

Опыт Джоуля

При открытии крана газ переходит из сосуда 1 в сосуд 2. Такое расширение газа не приводит к заметному изменению Т жидкости, т.е. 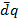=0; При таком расширении никакая работа не совершается =>

Пусть Т=const => dU – полный дифференциал (1.15);

dU= =0

dV≠0 =>

(1.22)

Т.о. внутренняя энергия газа при постоянной Т не зависит от V.

Уравнение 1.22 справедливо для идеальных газов.

Для реальных газов величина ≠0

Учтем также, что T=const

(1.23)

Молекулы идеального газа не взаимодействуют друг с другом => энергия остается неизменной при изменении расстояния между молекулами.

Уравнения 1.22 и 1.23 являются выражениями закона идеальных газов и выводятся из IIЗакона термодинамики, применив закон идеальных газов.

Кроме того учтем для идеальных газов

Тогда разность 1.21 теплоемкостей приобретает вид

(1.24)

Общее выражение для газов будет получено с помощью II закона термодинамики.

Вообще говоря, чем сложнее молекула, тем больше её мольная теплоёмкость и тем больше влияние Т.

Зависимость от Т для пара газов.

Мольную теплоёмкость простых газов можно с большой точностью вычислить метеорологических данных, чем непосредственно измерить в эксперименте, особенно при высоких Т.

Для вычисления теплоты поглощаемой 1 молем при нагревании газа от Т₁ до Т₂, удобно представить как функцию Т.

Эмпирическое уравнение применимо в диапазоне Т 300-1500К

Теплоемкость твердых тел см. ФТТ

особенно полезно для расчета С твердого тела при Т<15К

Примеры:

1)Молекулярные кристаллы, в частности кристаллы инертных газов. Энергия взаимодействия двух частиц может быть представлена

Запишем потенциал в более красивой форме

имеем потенциал Ленарда Джонса.

Этот потенциал описывает свойства газообразных Ne-Xe (атомы не деформируются при объединении в тв. т.)

Параметры подобрать так, чтобы они позволяли хорошо описывать термодинамические свойства газов. А затем использовать те же параметры для описания свойств твердых тел, сопоставив результаты с экспериментом.

2)Ионные кристаллы.

Полная энергия ионного кристалла в состоянии равновесия

(если силы отталкивания )

– равновесное состояние между ионами

постоянная Манделунга

константа, определяемая природой кристалла (справедливость подобного выражения подвергается проверке с помощью термодинамического цикла Габера-Борна)

Рассматривается 1 моль NaCl. Переводится это кол-ва вещества из кристаллического состояния в пар (ионный и атомный) Для вычисления теплоты используем теплоемкость. Зная теплоту реакции можно определить U.

Термохимия

1.10.1 Определения.

В термохимии предметом рассмотрения является теплота, поглощаемая или выделяемая в химических реакциях (1), при разовых превращениях (2) или при разбавлении растворов (3).

Экзотермические реакции протекают с выделением q и

Эндотермические реакции протекают с поглощением q и

Изменение в химических реакциях зависит от того, в каком состоянии находится вещества и продукты реакции.

Например, теплота сгорания графита ≠ теплоте сгорания алмаза.

Значение термодинамических свойств обычно приводятся для стандартных состояний.

Стандартное состояние газа – это идеальный газ при P=1атм и данной Т, стандартное состояние твердого тела – это характерное кристаллическое состояние при P=1атм и данной Т, например, графит для углерода.

Стандартное состояние растворенного вещества – это концентрация, при которой активность = 1.

Температуру следует указать особо, т.к термодинамические функции табулируются при Т=25⁰С.

Термодинамические функции в стандартном состоянии помечаются верхним индексом «⁰».

Уже знаем, что теплота, поглощенная при P=const в реакциях где единственным видом произведенной роботы является работа расширения = , т.е. разности энтальпий продуктов реакции, указных в правой части уравнения, в их конечном состоянии Н₁-Н данного числа молей реагирующих веществ, указанных слева, в их начальном состоянии. Можно определить только изменение Н, но не их абсолютные значения.

Калориметрические изменения

Теплота, выделяемая или поглощаемая в химической реакции измеряется с помощью калориметра. Наиболее распространенный тип калориметра представляет собой камеру, в которой протекает реакция, а камера помещенная в сосуд, заполнена известным количеством воды. Повышение температуры воды измеряется чувствительным термометром произведение (С_воды+С_калор) выделившейся.

С_воды: m_воды*С_уд

С_калор.: в калориметре проводят реакцию с известным тепловым эффектом.

Для термохимических измерений пригодны только реакции, которые проходят быстро и до конца, теплота сгорания в термохимии имеет наибольшее значение.

Сравнение различного типа реакций проводят по величине изменения стандартной энтальпии в данной реакции при 25⁰С 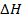⁰.

Колориметрические реакции бывают двух типов:

1) В калориметре с V=const: работа не производится, => поглощается приросту внутренней энергии.

2) В калориметре с P=const: I закон

Количества теплоты , поглощаемые в обоих экспериментах отличаются.

Задача 5

Теплота сгорания СО в калориметре с постоянным объемом равна -67,370 ккал/моль.

Вычислить теплоту сгорания в калориметре с постоянным давлением при допущении, что газы идеальны.

СО(газ)+1/2О₂(газ)=СО₂(газ)

В других типах калориметрических измерений выделяется очень маленькие количества теплоты и поэтому применяют чувствительные дифференциальные методы (термисторы) некоторые специальные калориметры имеют чувствительность в 1 мккал. Такие калориметры можно использовать для измерения теплоты, выделяющейся в реакциях с участием белков и полинуклеидов.

Теплоты сгорания имеют практическое значение, а не только теоретическое.

(Например, для того, чтобы человеку полностью израсходовать энергию, полученную от 1 свиного шницеля нужно 2 часа убирать снег, в то время как 10 минут плавания по энергии эквивалентны 1 яблоку.)

Пример:

1)Покупатель должен знать теплоту сгорания 1г угля.

2)Врач-диетолог должен знать число ккал, получаемое при сгорании различных видов пищи.

Глава 1.

Первый закон термодинамики.

Введение

Количественные характеристики: температура, работа, внутренняя энергия и теплота.

Обсуждается научное понятие температуры.

Принцип, на котором основывается определение температуры найден после установления I и II законов термодинамики и поэтому называется нулевым законом.

I закон выражает идею сохранения энергии, которая сначала возникла в механике, потом распространилась на электростатику и электродинамику.

Опыты Джоуля в 1840-1845 показали, что можно включить теплоту в закон сохранения энергии.

I закон вводит понятие внутренней энергии.

1. Система, окружающая среда, состояние системы и параметры состояния.

Термодинамическая система– это рассматриваемая часть материальной вселенной. Она отделена от окружающей среды замкнутой поверхностью – границей.

Система называется изолированной, если эта граница исключает любые взаимодействия с окружающей средой.

Система называется открытой, если через границу переходит вещество, и система называется закрытой, если нет. При этом теплота может поступать в закрытую систему или выделяться из неё.

Система может претерпеть изменения, переходя от начального состояния к конечному, при которых она обменивается теплотой и работой с окружающей средой; при этом изменяется как система, так и окружающая среда. Если граница не пропускает теплоту, то любой процесс, происходящий в системе называется адиабатическим, а границу – адиабатической оболочкой.

Если при данных условиях система является равновесной, то говорят, что она находится в некотором определенном состоянии, то есть каждое из ее свойств имеет конкретное численное значение.

Установлено, что для данного количества газа или жидкости. Состояние полностью определяется двумя переменными из трех: p, V, T. Эти переменные называются параметрами состояния.

Термодинамика имеет дело с переходами от некоторого начального состояния к некоторому конечному. При этом переходе может происходить теплообмен и совершаться работа над системой или окружающей средой.

1.2 Нулевой закон термодинамики. Температурная шкала.

Для определения понятия температуры нужно ввести понятие теплового равновесия.

Приводим в тепловой контакт две закрытые системы. Свойства обоих систем будут изменяться до такого состояния, когда дальнейшие изменения ужу не происходят. Это и есть состояние теплового равновесия.

Чтобы установить, находятся ли две системы при одной и той же температуре, надо привести системы в соприкосновение и посмотреть, изменяются ли их свойства.

Отсутствие изменений свидетельствует о том, что системы находятся при одинаковой T.

Нулевой закон.

Рассмотрим 3 системы: A, B, C.

Экспериментально установим, что если тело A и тело B находится в тепловом равновесии с телом C, то A и B находятся в тепловом равновесии друг с другом. Этот экспериментальный факт называется нулевым законом термодинамики.

Другая формулировка нулевого закона термодинамики:

Если две системы находятся в тепловом равновесии друг с другом, то их температуры одинаковы, если не находятся в тепловом равновесии - то их температуры различны.

Температурная шкала.

Пусть тело B находится в состоянии, характеризующимся (V_B и P_B) B óA (V_A и P_A), P_a,V_a – переменные, но ó сохраняется.

Пусть тело A (газ, жидкость) находятся в равновесии с B, P_a и V_a определяются из опыта.

Существует много сочетаний P_a и V_a , соответствующих равновесию. Эти пары значений образуют график зависимости P_a от V_a. Полученная кривая называется изотермой и согласно нулевому закону не зависит от природы тела B. Так как заменив тело B любым иным телом, находящимся в равновесии с B, мы получим тот же результат.

Изменив тепловое состояние B и повторив опыт мы получим другую изотерму для A.

Каждой найденной изотерме можно приписать некоторую 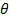температуру и таким образом построить температурную шкалу.

Тела с одинаковой 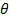сохранят неизменными все свойства, если их привести в тепловой контакт друг с другом через поверхность раздела, которая позволяет им иметь любые давления и любой химический состав.

Существует много температурных шкал, но самая полезная основана на поведении идеальных газов. Оно получено экстраполяцией поведения реальных газов с нулевым давлением к нулевому давлению. Температурная шкала идеального газа тождественна той шкале, которую дает статистическая механика.

Изотермы для вещества A. Для другого вещества это график может выглядеть иначе.

Пары переменных P и V, составляющие одной и той же T м. б. представлены в виде некоторой функции (например кривые на рисунке 1.1)

f(P,V)=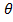

(1.1)

Уравнения такого типа называются уравнениями состояния для газа или жидкости .

У любого реального газа (жидкости) свое уравнение состояния.

Из (1.1) следует, что существует функция состояния вещества называемая температурой, которая имеет одинаковое значение для тел, находящихся в тепловом равновесии друг с другом.

Используем наши знания о поведении газов при низких P (например, закон Бойля).

По мере понижения P данного количества газа он всё точнее подчиняется уравнению

PV=k (T const)

(1.2)

А произведение PV (газов) экстраполированное к нулевому давлению ~ число n молей газа к функции температуры 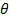=T

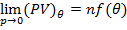
(1.3)

Пусть 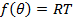, где R - газовая постоянная, T – температура идеального газа

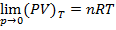
(1.3')

(Для идеального газа PV=nRT)

Чтобы теперь построить температурную шкалу требуется определить значение T какого-нибудь стандартного состояния, чтобы можно было вычислить газовую постоянную R.

Напоминание

Единица измерения т.д. T – градус K в системе СИ установлена следующим образом: отсчет по шкале начинается от абсолютного нуля, а T=273,1600 приписывается тройной точке воды (лед, жидкость и пар находятся в равновесии в отсутствии воздуха)

T плавления льда (T, при которой лед и вода в равновесии в присутствии воздуха при Р=1 атм.) дает «0» на шкале С.

Этой точке приписана Т на 0.0100⁰С ниже Т тройной точки воды, то есть 273, 1500К.

Т.о. т.д.Т связана с t по C: t=T-273,1500.

Универсальная газовая постоянная R.

Тщательные эксперименты с молекулярным кислородом показывают, что при P ->0. Произведение PV для 1моля кислорода (31, 9988)-> 22,41383 л*атм при 0⁰ С (273,1500К)

Можно вычислить R и посредством (1.3)

Надо вспомнить систему СИ:

Стандартная атмосфера равна давлению ртутного столба h=76см при 0⁰С в точке Земли, где g=9,80665м/с², ρ_Hg=13,5951г/см³

Тогда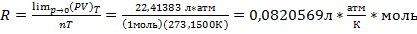

В системе СИ ед. [P]=Па=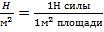

Давление одной стандартной атмосферы в Па можно вычислить

P=(0,76см)(13,5951*10³ кг/м³)(9,80665м/с²)=101325 Па=101325Н/м²

P - давление есть сила, приходящаяся на 1 единицу площади.

Размерности:

[P*V]=[F*l]=[w]=[E]

R можно выразить в [Дж]

R=PV/nT=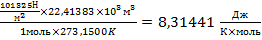

Удобно пользоваться законом идеальных газов в расчете на 1 моль газа

PV=RT, где V с «чертой»

(1.4)

V - объем, приходящийся на 1 моль газа.

Работа. Внутренняя энергия

1.3.1 Работа

В т.д-ке теплота и работа – алгебраические величины, они м.б. >0 и <0, сила – векторная величина.

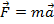
Сила которая сообщает массе m ускорение .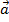

Работа ( 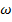) – скалярная величина.

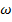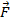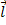=( , ) – скалярное произведение.

l – длина пути.

[w]=1Дж=Н*м

Бесконечно малое количество работы, совершенное силой f на пути dl:

fdl=PAdl=PdV,

(1.5)

т.о. бесконечно малое количество работы, производимое расширяющимся газом, которое сдвигает поршень на dl=PdV.

Работа – величина алгебраическая. Пусть 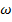>0, когда внешняя сила совершает работу над системой, 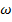<0 показывает, что над системой совершает работу над окружающей средой. (пример – см. рис. При расширении газа, давящего на поршень)

Внутренняя энергия. Опыты Джоуля.

Джоуль показал, что в адиабатических условиях данное количество работы всегда нагревает воду в калориметре на определенное число градусов, независимо от пути процесса, т.е. способа. (Эта работа затрачена на вращение мешалки с лопастями, проходящие j через R или на трение тел).

Определение: Данное изменение состояния в калориметре м.б. достигнуто любым способом, однако включающими одно и то же количество работы, или при любой последовательности операций, оно не зависит от пути процесса, а зависит от общего кол-ва работы.

Свойство системы, изменение которого рассчитывается таким способом, называется внутренней энергией U. Поскольку U системы можно увеличить, совершая над системой работ