Представление функции в виде интеграла фурье

Свойства

· Коммутативность: .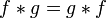

· Ассоциативность: .

· Линейность (дистрибутивность и умножение на число):

.

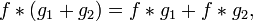
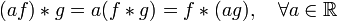· Правило дифференцирования: ,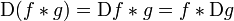

где обозначает производную функции по любой переменной.

· Свойство Фурье-образа: ,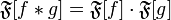

где обозначает преобразование Фурье функции .

Преобразование Фурье — операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.

Преобразование Фурье функции вещественной переменной является интегральным и задаётся следующей формулой:

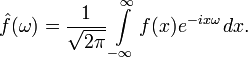
Разные источники могут давать определения, отличающиеся от приведённого выше выбором коэффициента перед интегралом, а также знака «−» в показателе экспоненты. Но все свойства будут те же, хотя вид некоторых формул может измениться.

60. преобразование Фурье

Преобразование Фурье — операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.Преобразование Фурье функции вещественной переменной является интегральным и задаётся следующей формулой:

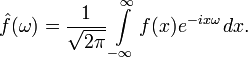
Свойства

Хотя формула, задающая преобразование Фурье, имеет ясный смысл только для функций класса 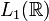, преобразование Фурье может быть определено и для более широкого класса функций и даже обобщённых функций. Это возможно благодаря ряду свойств преобразования Фурье:

· Преобразование Фурье является линейным оператором:

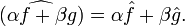
· Справедливо равенство Парсеваля: если 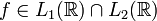, то преобразование Фурье сохраняет 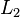-норму:

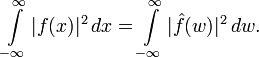
Это свойство позволяет по непрерывности распространить определение преобразования Фурье на всё пространство 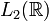. Равенство Парсеваля будет при этом справедливо для всех .

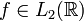· Формула обращения:

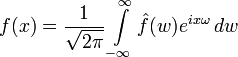
справедлива, если интеграл в правой части имеет смысл. В частности, это верно, если функция является достаточно гладкой. Если 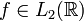, то формула также верна, поскольку равенство Парсеваля позволяет придать интегралу в правой части смысл с помощью предельного перехода.

Эта формула объясняет физический смысл преобразования Фурье: правая часть — (бесконечная) сумма гармонических колебаний с частотами 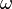, амплитудами 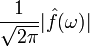и фазовыми сдвигами 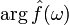соответственно.

· Теорема о свёртке: если 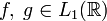, тогда

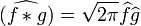, где

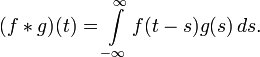
Эта формула может быть распространена и на случай обобщённых функций.

· Преобразование Фурье и дифференцирование. Если 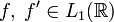, то

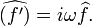
Из этой формулы легко выводится формула для 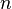-й производной:

Формулы верны и в случае обобщённых функций.

· Преобразование Фурье и сдвиг.

Эта и предыдущая формула являются частными случаями теоремы о свёртке, так как сдвиг по аргументу — это свёртка со сдвинутой дельта-функцией 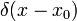, а дифференцирование — свёртка с производной дельта-функции.

· Преобразование Фурье и растяжение.

· Преобразование Фурье обобщённых функций. Преобразование Фурье можно определить для широкого класса обобщённых функций. Определим вначале пространство гладких быстро убывающих функций (пространство Шварца):

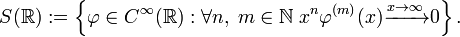
Ключевым свойством этого пространства является то, что это инвариантное подпространство по отношению к преобразованию Фурье.

Теперь определим его двойственное пространство . Это некоторое подпространство в пространстве всех обобщённых функций — так называемые обобщённые функции медленного роста. Теперь для функции 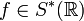её преобразованием Фурье называется обобщённая функция 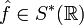, действующая на основные функции по правилу

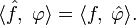
Например, вычислим преобразование Фурье дельта-функции:

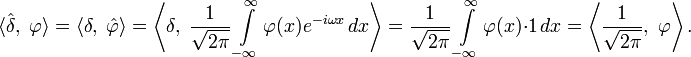
Таким образом, преобразованием Фурье дельта-функции является константа .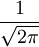

В-функция и её своиства

бета-функцией ( 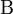-функцией, бета-функцией Эйлера или интегралом Эйлера I рода) называется следующаяспециальная функция от двух переменных:

,

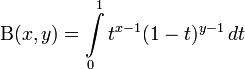определённая при , .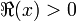

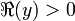Бета-функция была изучена Эйлером и Лежандром ^{[когда?]}, а название ей дал Жак Бине.

Свойства

Бета-функция симметрична относительно перестановки переменных, то есть

.

Бета-функцию можно выразить через другие функции:

,

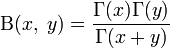где 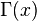— Гамма-функция;

;

;

,

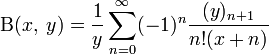где 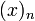— нисходящий факториал, равный .

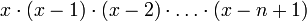Подобно тому как гамма-функция для целых чисел является обобщением факториала, бета-функция является обобщением биномиальных коэффициентов с немного изменёнными параметрами:

.

Гамма функция и её свойства

Г(p)=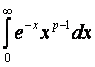

Непрерывность

Г-функция

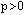
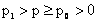
сходящийся (по признаку Вейерштрасса)

=> равномерная сходимость по параметру, => подынтегральная функция непрерывна, => интеграл сходится к непрерывной функции,

=> Г-функция непрерывна

Формулы понижения степени

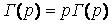
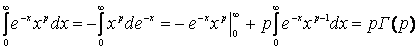
Если n – натуральное число, то

53. Интегрирование несобственных интегралов, зависящих от параметров.

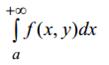(7)

и

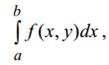(а − особая точка) (8)

называются сходящимися равномерно по переменной у, принадлежащей неко-

торой области U, если они сходятся при любом фиксированном значении y ∈U

и величина δ в критерии сходимости несобственного интеграла (см. п. 3.3) не

зависит от значения у, т.е.

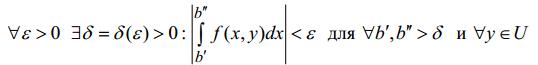− для интеграла (7),

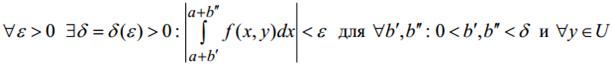− для интеграла (8).

Сформулируем свойства равномерно сходящегося интеграла (7). (Ана-

логичные свойства справедливы и для интеграла (8)):

Если функция f(х, у) непрерывна при х ≥ а и c ≤ у ≤ d и интеграл (7)

сходится равномерно при c ≤ у ≤ d, то функция

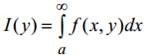непрерывна по у при c ≤ у ≤ d.

При условиях, сформулированных в свойстве 1, справедлива формула

интегрирования под знаком интеграла:

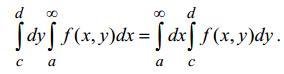
52. Дифференцирование несобственных интегралов, зависящих от параметров.

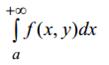(7)

и

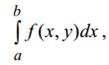(а − особая точка) (8)

называются сходящимися равномерно по переменной у, принадлежащей неко-

торой области U, если они сходятся при любом фиксированном значении y ∈U

и величина δ в критерии сходимости несобственного интеграла (см. п. 3.3) не

зависит от значения у, т.е.

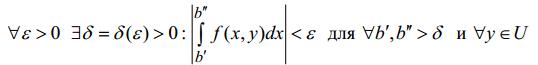− для интеграла (7),

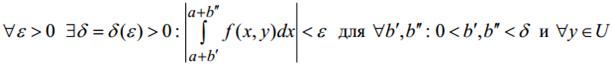− для интеграла (8).

Сформулируем свойства равномерно сходящегося интеграла (7). (Ана-

логичные свойства справедливы и для интеграла (8)):

Если функция f(х, у) непрерывна при х ≥ а и c ≤ у ≤ d и интеграл (7)

сходится равномерно при c ≤ у ≤ d, то функция

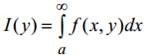непрерывна по у при c ≤ у ≤ d.

Если функции f(x,y) и y f ′ (x,y) непрерывны, несобственный интеграл(7) сходится, а интеграл 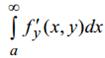сходится равномерно, то имеет место формула дифференцирования под знаком интеграла:

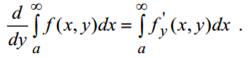
Аддитивность

Циркуляция по контуру, ограничивающему несколько смежных поверхностей, равна сумме циркуляций по контурам, ограничивающим каждую поверхность в отдельности, то есть

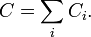
Формула Стокса

Циркуляция вектора F по произвольному контуру Г равна потоку вектора 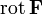через произвольную поверхность S, ограниченную данным контуром.

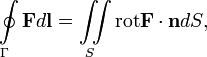
где 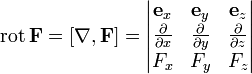— ротор (вихрь) вектора F.

В случае, если контур плоский, например лежит в плоскости OXY, справедлива теорема Грина

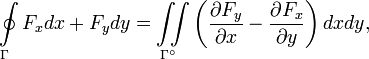
где 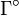— плоскость, ограничиваемая контуром 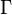(внутренность контура).

Если F — некоторое силовое поле, тогда циркуляция этого поля по некоторому произвольному контуру Γ есть работа этого поля при перемещении точки вдоль контура Г. Отсюда непосредственно следует критерий потенциальности поля: поле является потенциальным когда циркуляция его по произвольному замкнутому контуру есть нуль. Или же, как следует из формулы Стокса, в любой точке области D ротор этого поля есть нуль.

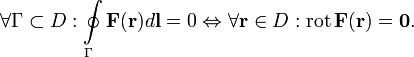
44. Поток векторного поля и его вычисление

Понятие потока векторного поля удобно рассматривать на примере потока жидкости, движущейся через некоторую поверхность. Объем жидкости, протекающей в единицу времени через поверхность, расположенную в движущейся жидкости, назовем потоком жидкости через эту поверхность.

Пусть поверхность S расположена в поле скоростей частиц несжимаемой жидкости с плотностью ρ = 1. Можно показать, что поток векторного поля в этом случае равен

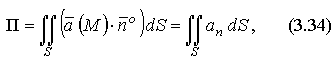
где 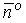– единичный нормальный вектор к поверхности S, расположенный по одну сторону с вектором , а величина .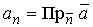

Независимо от физического смысла вектора интеграл (3.34) по поверхности называют потоком векторного поля через поверхность S.

Пусть 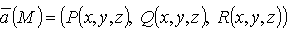и 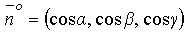тогда поток П вектора через поверхность S можно записать в виде:

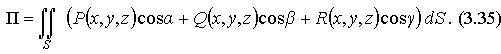
Или учитывая связь поверхностных интегралов первого и второго родов, можно записать поток П через поверхностный интеграл в координатах:

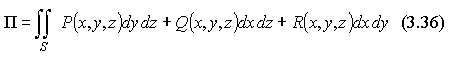
ПРИМЕР 1. Ориентированные поверхности.

Непосредственное вычисление потока. Поскольку поток векторного поля определен с помощью поверхностного интеграла, вычисление потока сводится к вычислению такого интеграла от функции 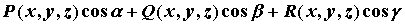, где 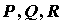- компоненты векторного поля, 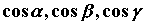- направляющие косинусы вектора нормали.

Свойства

1. Линейность: ;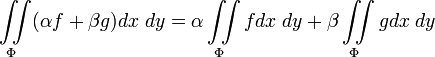

2. Аддитивность: ;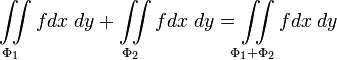

3. При изменении ориентации поверхности, поверхностный интеграл меняет знак.

38. Формула Гаусса-Остроградского и её приложения к вычислению поверхностных интегралов и объемов пространственной области.

Тройной интеграл после вычисления первого внутреннего интеграла превращается в двойной интеграл, который можно выразить через поверхностный.

Имеем тело ограниченное гладкими поверхностями : G1 – низ ,

z = z0(x,y) ; G2 – верх, z = Z(x,y) ; G3 - цилиндрическая боковая поверхность по границе области D на плоскости хОу. В этом объеме V определена функция R(x,y,z) , причем, функция и ее производные непрерывны. Рассмотрим интеграл

J= 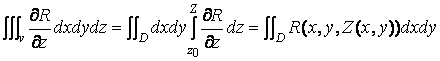- - 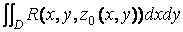= J1 – J2

По формуле ( 13 ) интеграл J1 сводится к интегралу по внешней поверхности «верха» тела, а J2 по внутренней поверхности «низа». При переходе на внешнюю сторону «низа» знак J2 меняется. Учтем также, что аналогичный интеграл J3 по боковой поверхности G3 равен нулю, т.к. площадь ее проекции на плоскость хОу равна нулю. В итоге имеем

J = + +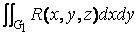

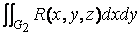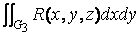
где интегралы вычисляются по внешней стороне поверхности ограничивающей тело, или

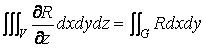( 18 )

Обобщение формулы ( 18 ) на случай тела произвольной формы приводит к формуле Остроградского – Гаусса

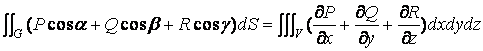( 19 )

которая интеграл по объему заменяет на интеграл по внешней стороне поверхности ограничивающей тело.

Вычисление объема.

Пусть подынтегральная функция в ( 4 ) не зависит от z , тогда она определяет некоторую поверхность z = f(x,y) , а интеграл по D объем цилиндрического бруса, ограниченного этой поверхностью и областью D . Переход к поверхностному интегралу в этом случае дает следующее выражение для объема цилиндрического бруса V = 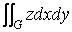( 14 ) Понятие о комплексных числах. Определение. Комплексным числом z называется выражение 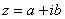, где a и b – действительные числа, i – мнимая единица, которая определяется соотношением: При этом число a называется действительной частью числа z (a = Re z), а b- мнимой частью (b = Im z).

Обобщение этой формулы на случай тела произвольной формы ограниченного поверхностью G имеет вид V = 1/3 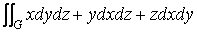( 15 )

36. Поверхностный интеграл 1-го рода, Его свойства. Вычислительная форма

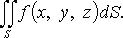
Сведение к двойному

1. Поверхность S задана уравнением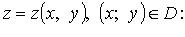

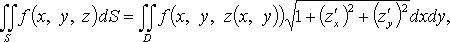
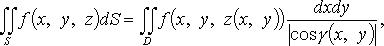
где 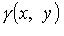- величина угла между нормалью к поверхности и положительным направлением оси Oz.

2. Поверхность S задана параметрически: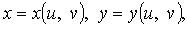

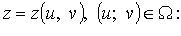
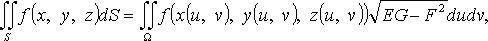
где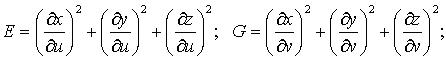

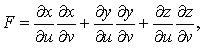или

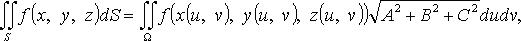
где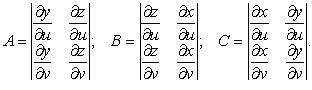

Свойства

1. Линейность: ;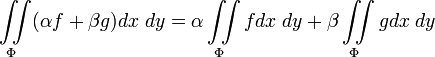

2. Аддитивность: ;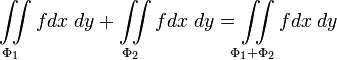

3. При изменении ориентации поверхности, поверхностный интеграл меняет знак.

33. Явные представления поверхности

32. Касательная плоскость и нормаль к поверхности

Пусть поверхность 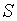задана уравнением 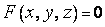(1)

в неявном виде. Будем считать, что 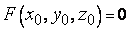и в некоторой окрестности точки 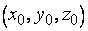функция 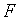имеет непрерывные частные производные, одновременно не равные нулю. Тогда

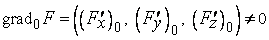(2)

Мы пишем 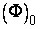вместо .

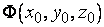Для определенности предположим, что 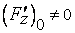. Тогда на основании теоремы о неявной функции существует окрестность точки 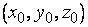, в которой поверхность 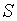описывается явно непрерывно дифференцируемой функцией 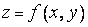. Уравнение касательной плоскости к 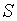в точке 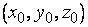, как мы знаем, имеет вид

,

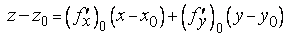где

.

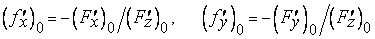В силу этого уравнения касательной плоскости к 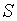в точке 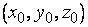запишется так:

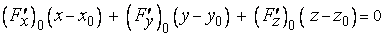, (3)

а уравнение нормали к 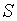в точке 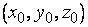- так:

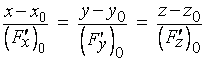. (4)

Те же уравнения (3), (4) мы получим, если предположить, что 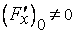или 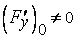. В этих случаях в окрестности 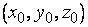поверхность 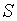описывается явно соответственно уравнениями

.

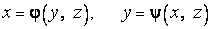Мы видим, что при условии (2) поверхность 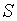в любой точке 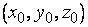имеет касательную плоскость, непрерывно изменяющуюся при непрерывном передвижении точки 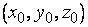. Такую поверхность называют гладкой поверхностью .

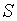Другое дело, если 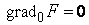. В этом случае нельзя гарантировать, что в точке 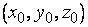существует касательная плоскость к . Она может существовать, а может и не существовать.

31. Ориентация гладкой поверхности

Гладкая поверхность ориентируема, если можно построить на ней непрерывное поле единичных нормальных векторов. Это поле единичных нормалей определяет ориентацию (или сторону) поверхности. На простой гладкой поверхности всегда определено непрерывное поле единичных нормальных векторов:

Произвольные гладкие поверхности могут быть как ориентируемыми (двусторонними), как и неориентируемыми (односторонними).Лист Мёбиуса.

26. Независимость криволинейного интеграла второго рода от пути интегрирования. Признак Грина

Пусть D - некоторая замкнутая область на плоскости хОу, ограниченная контуром L. На ней заданы функции Р = Р(х,у) и Q = Q(x,y), непрерывные на D вместе со своими частными производными первого порядка. Формула Грина связывает криволинейный интеграл второго рода по L с двойным интегралом по области D:

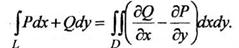
Движение по контуру L - в положительном направлении.

С помощью формулы Грина значение криволинейного интеграла по замкнутому контуру можно найти, вычислив двойной интеграл.

20. Формула Грина для многосвязной области

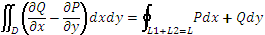
Формулу Грина можно применять, если область D – замкнутая, ограниченная кусочно-гладким контуром L, функции P(x,y) и Q(x,y) непрерывны и имеют частные производные первого порядка: 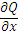и .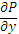

19. Формула Грина для односвязной области

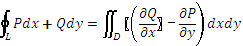
Формулу Грина можно применять, если область D – замкнутая, ограниченная кусочно-гладким контуром L, функции P(x,y) и Q(x,y) непрерывны и имеют частные производные первого порядка: 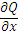и .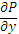

15. Криволинейный интеграл 1-го рода и его свойства. Вычислительная формула

Определение: Если при ∆l→0, σ имеет конечный предел, не зависящий ни от способа разбиений, ни от выбора точек Mk, то этот предел называется криволинейным интегралом первого рода от функции f(M) по кривой AB (интегрируется по длине дуги кривой) и обозначается 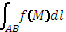или 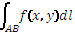. Таким образом .

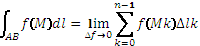Свойства: 1) Криволинейный интеграл первого рода не зависит от направления интегрирования; 2) Линейность; 3) Аддитивность; 4) Если f(M)≥0, то 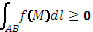; 5) f(M) интегрируема на АВ, следовательно |f(M)| тоже интегрируем на кривой АВ; 6) Среднее значение: 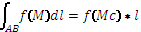, где l – длина кривой.

Способы вычисления криволинейного интеграла: 1) Кривая АВ: 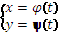, t0≤t≤t1, A→t=t0, B→t=t0, 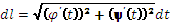, 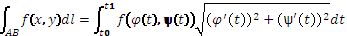; 2)АВ: y=y(x), a≤x≤b, A→x=a, B→x=b, ,

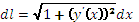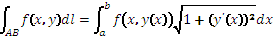
14. Физические приложении тройного интеграла

Тензор инерции

Используя рассмотренные выше 6 чисел I_x, I_y, I_z, I_xy, I_xz, I_yz, можно составить так называемую матрицу инерции или тензор инерции тела:

Вычисление площадей

Вычисление объёмов тел

Свойства

· Коммутативность: .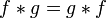

· Ассоциативность: .

· Линейность (дистрибутивность и умножение на число):

.

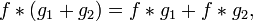
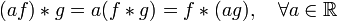· Правило дифференцирования: ,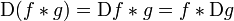

где обозначает производную функции по любой переменной.

· Свойство Фурье-образа: ,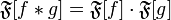

где обозначает преобразование Фурье функции .

Преобразование Фурье — операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.

Преобразование Фурье функции вещественной переменной является интегральным и задаётся следующей формулой:

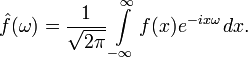
Разные источники могут давать определения, отличающиеся от приведённого выше выбором коэффициента перед интегралом, а также знака «−» в показателе экспоненты. Но все свойства будут те же, хотя вид некоторых формул может измениться.

60. преобразование Фурье

Преобразование Фурье — операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.Преобразование Фурье функции вещественной переменной является интегральным и задаётся следующей формулой:

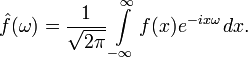
Свойства

Хотя формула, задающая преобразование Фурье, имеет ясный смысл только для функций класса 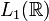, преобразование Фурье может быть определено и для более широкого класса функций и даже обобщённых функций. Это возможно благодаря ряду свойств преобразования Фурье:

· Преобразование Фурье является линейным оператором:

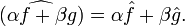
· Справедливо равенство Парсеваля: если 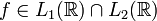, то преобразование Фурье сохраняет 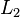-норму:

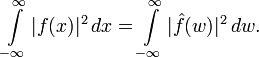
Это свойство позволяет по непрерывности распространить определение преобразования Фурье на всё пространство 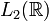. Равенство Парсеваля будет при этом справедливо для всех .

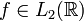· Формула обращения:

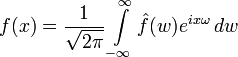
справедлива, если интеграл в правой части имеет смысл. В частности, это верно, если функция является достаточно гладкой. Если 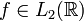, то формула также верна, поскольку равенство Парсеваля позволяет придать интегралу в правой части смысл с помощью предельного перехода.

Эта формула объясняет физический смысл преобразования Фурье: правая часть — (бесконечная) сумма гармонических колебаний с частотами 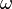, амплитудами 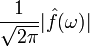и фазовыми сдвигами 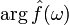соответственно.

· Теорема о свёртке: если 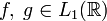, тогда

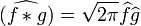, где

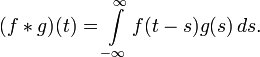
Эта формула может быть распространена и на случай обобщённых функций.

· Преобразование Фурье и дифференцирование. Если 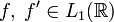, то

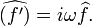
Из этой формулы легко выводится формула для 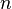-й производной:

Формулы верны и в случае обобщённых функций.

· Преобразование Фурье и сдвиг.

Эта и предыдущая формула являются частными случаями теоремы о свёртке, так как сдвиг по аргументу — это свёртка со сдвинутой дельта-функцией 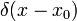, а дифференцирование — свёртка с производной дельта-функции.

· Преобразование Фурье и растяжение.

· Преобразование Фурье обобщённых функций. Преобразование Фурье можно определить для широкого класса обобщённых функций. Определим вначале пространство гладких быстро убывающих функций (пространство Шварца):

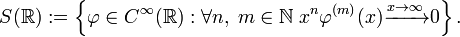
Ключевым свойством этого пространства является то, что это инвариантное подпространство по отношению к преобразованию Фурье.

Теперь определим его двойственное пространство . Это некоторое подпространство в пространстве всех обобщённых функций — так называемые обобщённые функции медленного роста. Теперь для функции 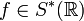её преобразованием Фурье называется обобщённая функция 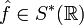, действующая на основные функции по правилу

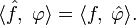
Например, вычислим преобразование Фурье дельта-функции:

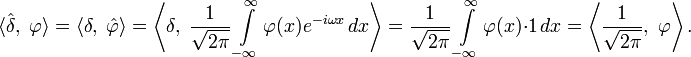
Таким образом, преобразованием Фурье дельта-функции является константа .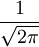

Представление функции в виде интеграла фурье

Формула

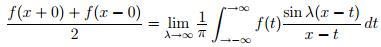имеет место, если

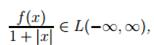
И в некотором интервале, содержащем точку x внутри, функция f(t) имеет ограниченное изменение или удовлетворяет какому-либо другому условию сходимости ряда или интеграла Фурье.

Д о к а з а т е л ь с т в о. достаточно доказать существование столь большого T, что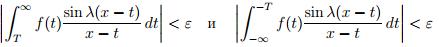

для всех значений λ > λ0. Очевидно, это имеет место при выполненииусловия I. Далее, убедимся в справедливости.

Остается доказать достаточность условия. Положим Тогда 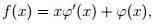и требуемый результат следует из того, что xϕ(x) удовлетворяет условию.

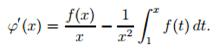
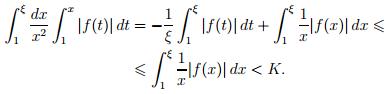
и так как f(t)/t, по условию I, принадлежит к L(1,∞), то правая часть этого равенства стремится к нулю.

В-функция и её своиства

бета-функцией ( 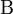-функцией, бета-функцией Эйлера или интегралом Эйлера I рода) называется следующаяспециальная функция от двух переменных:

,

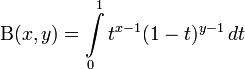определённая при , .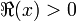

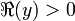Бета-функция была изучена Эйлером и Лежандром ^{[когда?]}, а название ей дал Жак Бине.

Свойства

Бета-функция симметрична относительно перестановки переменных, то есть

.

Бета-функцию можно выразить через другие функции:

,

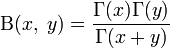где 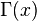— Гамма-функция;

;

;

,

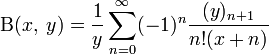где 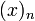— нисходящий факториал, равный .

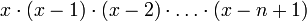Подобно тому как гамма-функция для целых чисел является обобщением факториала, бета-функция является обобщением биномиальных коэффициентов с немного изменёнными параметрами:

.