Течение и свойства жидкостей

1. Идеальная жидкость. Основные определения. Движение идеальной жидкости. Уравнение неразрывности. Уравнение Бернулли.

2. Движение вязкой жидкости. Уравнение Ньютона. Формула Пуазейля.

3. Модель кровообращения Франка. Электрическая модель кровообращения. Пульсовая волна. Формула Моенса-Кортевега.

1. Система кровообращения человека служит для постоянного снабжения клеток питательными веществами и газами, для обмена продуктами жизнедеятельности клеток, а также переноса тепла. Она представляет собой разветвленную и замкнутую цепь сосудов различного калибра. В этом она сходна с водопроводной системой, также предназначена для обмена водой и теплом между источником и многочисленными потребителями. В обеих системах движущей силой является давление, создаваемое на входе в систему и в участках выхода. Этой цели служит генератор давления, которым в системе кровообращения является сердце, а в водопроводной системе – насос.

Движение жидкости или крови всегда происходит от участка с более высоким давлением к участку со сниженным давлением, поэтому движение крови подчиняется тем же закономерностям, которые определяют движение жидкости в любой гидродинамической системе.

Воображаемая жидкость, совершенно не обладающая вязкостью, называется идеальной. Уравнение неразрывности: произведение площади поперечного сечения трубки на скорость движения жидкости есть величина постоянная:

(1)

Пусть по наклонной трубке тока переменного сечения движется жидкость в направлении слева направо. Мысленно выделим область трубки, ограниченную сечениями и в которых скорости течения равны соответственно и .

Определим изменение полной энергии в этой области за промежуток времени 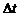. За это время масса жидкости, заключенная между сечениями и , втекает в рассматриваемую область, а масса, заключенная между и , вытекает из нее.

Полная энергия жидкости

(2)

Или (3)

должно равняться работе внешних сил по перемещению массы 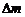: = (4)

Определим . Внешняя сила давления F₁ совершает работу по перемещению втекающей массы на пути ; в то же время вытекающая масса совершает работу против внешней силы F₂ на пути , поэтому

, , .

Учитывая, что и , где P₁ и P₂ - давления на сечениях S₁ и S₂, получим:

, но ,

где -объем каждой из рассматриваемых масс, поэтому (5)

Объединяя формулы 3, 4, 5, получим:

.

Поделив обе части на и учитывая, что , получим:

.

Поскольку S₁ и S₂ выбраны произвольно, то

- уравнение Бернулли

В идеальной несжимаемой жидкости сумма динамического, гидравлического и статического давлений постоянна на любом поперечном сечении потока.

Для горизонтальной трубки уравнение Бернулли принимает вид .

Из уравнений Бернулли и неразрывности следует, что в местах сужения трубопровода скорость течения жидкости возрастает, а давление понижается.

2. При течении реальной жидкости отдельные слои ее воздействуют друг на друга с силами, касательными к слоям. Это явление называется внутренним трением или вязкостью.

Рассмотрим движение жидкости между двумя твердыми пластинками, из которых нижняя неподвижна, а верхняя движется со скоростью . Слой, прилипший ко дну, неподвижен. Максимальная скорость будет у слоя, «прилипшего» к верхней пластинке.

Сила внутреннего трения описывается уравнением Ньютона: ,

где - градиент скорости, S- площадь соприкасающихся слоев жидкости, 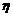- коэффициент вязкости.

Жидкости, подчиняющиеся уравнению Ньютона, называются ньютоновскими. Жидкости, не подчиняющиеся уравнению Ньютона, называются неньютоновскими. Вязкость ньютоновских жидкостей называют нормальной, неньютоновских - аномальной.

Кровь является неньютоновской жидкостью.

Примеры решения задач

1. В широкой части горизонтальной трубы вода течет со скоростью 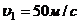. Определить скорость течения воды в узкой части трубы, если разность давлений в широкой и узкой ее частях равна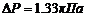

Решение:

Запишем уравнение Бернулли: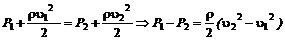

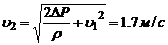
Формула Пуазейля

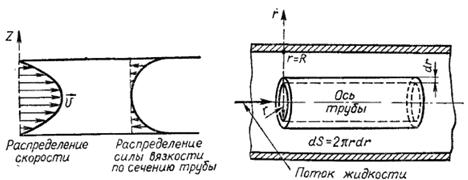
Наибольшей скоростью обладают частицы, движущиеся вдоль оси трубы; самый близкий к трубе слой жидкости неподвижен.

Для установления зависимости 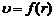выделим мысленно цилиндрический объем жидкости радиуса r и длины l. На торцах этого цилиндра поддерживаются давления P₁ и P_2, что обуславливает результирующую силу:

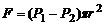_. (1)

На боковую поверхность цилиндра со стороны окружающего слоя жидкости действует сила внутреннего трения, равная

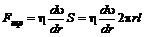_, (2)

где 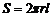- площадь боковой поверхности цилиндра.

F=F_тр 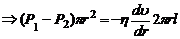(3)

Знак (-), так как 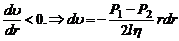. (4)

Проинтегрируем это уравнение:

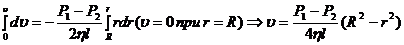. (5)

Наибольшую скорость имеет слой, текущий вдоль оси трубы (r=0):

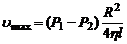
Определим объемную скорость течения жидкости Q. Для этого выделим цилиндрический слой радиусом r и толщиной dr. Площадь сечения этого слоя 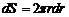. За 1с слой переносит объем жидкости

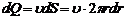(6)

Подставим (5) в (6), получим:

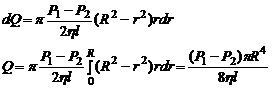(7)

(7) - Формула Пуазейля

Через трубу протекает тем больше жидкости, чем меньше ее вязкость и больше радиус трубы.

Формула Пуазейля аналогична закону Ома для участка цепи. Разность потенциалов соответствует разности давлений на концах трубы, сила тока - объемной скорости, электрическое сопротивление - гидравлическому сопротивлению:

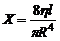. (8)

Гидравлическое сопротивление тем больше, чем больше вязкость 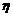, длина l трубы и меньше сечение.

Примеры решения задач

1. При чуме артерия сужается в 2 раза. Во сколько раз изменится объемная скорость кровотока?

Решение

По формуле Пуазейля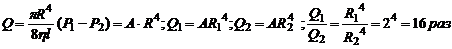

2. Каково гидравлическое сопротивление кровеносного сосуда длиной 0,12м и радиусом 0,1мм?

Решение:

Из формулы (8) для гидравлического сопротивления

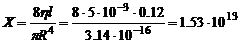
3. Модель кровообращения Франка

Модель позволяет установить связь между ударным объемом крови (объем крови, выбрасываемый желудочком за одну систолу), гидравлическим сопротивлением периферической части системы кровообращения х₀ и изменением давления в артериях. Артериальная часть системы кровообращения моделируется упругим (эластичным) резервуаром (УР).

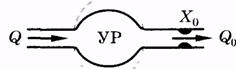
В УР (артерия) поступает кровь из сердца Q. От УР кровь оттекает со скоростью Q₀ в периферическую систему (артериолы, капилляры). Объем крови в УР зависит от P:

V=V₀+kP, (1)

где k - упругость резервуара;V₀ - объем УР при P=0. Из (1)

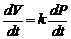(2)

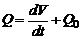(3),

т.е. объемная скорость кровотока из сердца равна скорости возрастания объема УР, т.е. скорости оттока крови из упругого резервуара.

На основании формулы Пуазейля и формулы (3) можно записать для периферии:

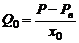, (4)

где P - давление в УР; P_в - венозное давление. При P_в = 0

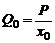(5)

Подставляя (2) и (5) в (3), получим:

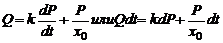(6)

Во время систолы (сокращение сердца) происходит расширение УР, во время диастолы - отток крови к периферии, Q=0. Тогда (6) перепишется:

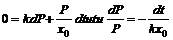(7)

Проинтегрировав (9), получаем зависимость давления в УР после систолы от времени:

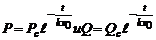(8)

На основе механической модели по аналогии можно построить электрическую модель.

Здесь источник U переменного электрического напряжения служит аналогом сердца, выпрямитель В - сердечного клапана.

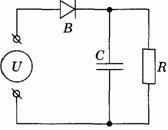
Конденсатор С в течение полупериода накапливает заряд, а затем разряжается на резистор R, так сглаживается сила тока через резистор. Действие конденсатора аналогично действию упругого резервуара, который сглаживает колебания давления крови в артериях и капиллярах. Резистор является электрическим аналогом периферической сосудистой системы.

Пульсовая волна - это распространяющаяся по аорте и артериям волна повышенного давления, вызванная выбросом крови из левого желудочка в период систолы.

Скорость пульсовой волны в крупных сосудах определяется формулой Моенса-Кортевега: 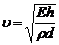, где Е - модуль упругости, 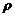- плотность вещества сосуда, h - толщина стенки сосуда, d-диаметр сосуда.

Примеры решения задач

1. Скорость пульсовой волны в артериях составляет 8 м/с. Чему равен модуль упругости этих сосудов, если известно, что отношение радиуса просвета к толщине стенки сосуда равно 6, а плотность крови равна 1150кг/м³?

Решение:

По формуле Моенса-Кортевега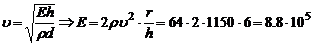

2. Определить среднюю линейную скорость кровотока в сосуде радиусом 1,5 см, если во время систолы через него протекает 60 мл крови. Длительность систолы считать равной 0,25с.

Решение:

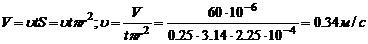
Лекция №3

Электростатика

1. Взаимодействие электрических зарядов в вакууме. Закон Кулона. Электрическое поле и его напряженность. Силовые линии электрического поля.

2. Электрический диполь. Поле диполя.

3. Теорема Остроградского-Гаусса.

4. Работа перемещения заряда в электрическом поле. Потенциал.

5. Использование электрических полей в медицине.

1. Электростатика изучает взаимодействие и условия равновесия покоящихся электрически заряженных тел, а также свойства этих тел, обусловленные электрическими зарядами.

Взаимодействие электрических зарядов осуществляется в соответствии с законом Кулона, который опытным путем установил, что два точечных заряда взаимодействуют в вакууме с силой F, пропорциональной величинам зарядов q₁ и q₂ и обратно пропорциональной квадрату расстояния r между ними и направленной по линии, соединяющей эти заряды:

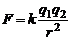, (1)

где k - коэффициент пропорциональности, 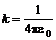, 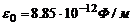- электрическая постоянная. Таким образом

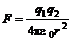(2)

Электрическим полем называется вид материи, посредством которого взаимодействуют электрические заряды.

Напряженность электрического поля в данной точке есть вектор, равный по величине силе, действующей на единичный положительный заряд, помещенный в эту точку и совпадающий с ней по направлению:

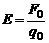(3)

Е измеряется в В/м.

Силовой линией электрического поля называется линия, в каждой точке которой касательная совпадает с вектором напряженности поля.

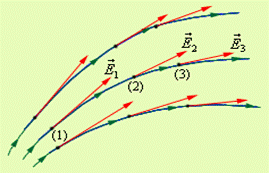
Электрическое поле называется однородным, если во всех его точках напряженность E одинакова. Напряженность электрического поля точечного заряда определяется формулой:

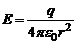, (4)

где r - расстояние от заряда, создающего поле, до точки, в которой определяется напряженность.

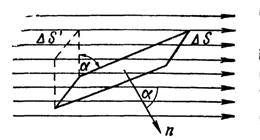
Число силовых линий, пронизывающих некоторую поверхность, расположенную в электрическом поле, называется потоком напряженности электрического поля N через эту поверхность:

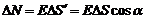(5),

где 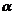- угол между силовой линией и нормалью n к площадке :

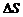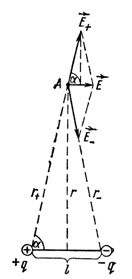
2. Электрический диполь. Поле диполя.

Электрическим диполем называется совокупность двух равных по величине разноименных точечных зарядов q, расположенных на некотором расстоянии друг от друга. Произведение P = ql называется моментом диполя, а l - его плечом. Дипольный момент направлен по оси диполя в сторону положительного заряда.

Напряженность поля на продолжении оси диполя

Напряженность поля вдоль оси диполя равна разности напряженностей Е⁺ и Е^-, создаваемых положительным и отрицательным зарядами: Е = Е⁺ - Е^-

Если r - расстояние от точки А до середины оси диполя, на основании (4) можно записать:

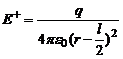и 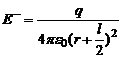. Тогда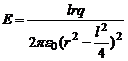

Полагая, что r >> l, пренебрежем 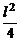. Тогда 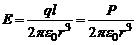(6)

Напряженность поля на перпендикуляре к середине оси диполя.

Напряженность Е в точке А равна Е = Е⁺ + Е^-. Так как r⁺ = r^- , то Е⁺ = Е^-, Тогда Е – диагональ ромба, 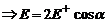. Но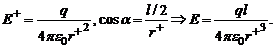

Полагая r>>l, r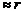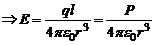⁺ (7)

Таким образом, на большом расстоянии от диполя напряженность электрического поля диполя обратно пропорциональна кубу расстояния.

3. Теорема Остроградского-Гаусса.

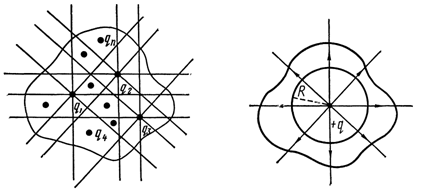
Определим поток напряженности поля электрических зарядов q_1, q_{2, …} q_n через некоторую замкнутую поверхность, окружающую эти заряды. Поток будем считать отрицательным, если он направлен внутрь поверхности, в противном случае – положительным

Рассмотрим сначала случай сферической поверхности радиусом R, окружающей один заряд q, находящийся в центре сферы. Согласно (4) напряженность поля на всей сфере одинакова и равна

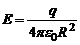. (8)

Силовые линии направлены по радиусам, т.е. перпендикулярно поверхности сферы. Это дает возможность применить для расчета потока напряженности N формулу

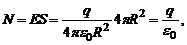(9)

где 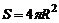- площадь сферической поверхности.

Окружим теперь сферу произвольной замкнутой поверхностью. Каждая силовая линия, пронизывающая сферу, пронижет и эту поверхность. Следовательно, формула (9) справедлива не только для сферы, но и для любой замкнутой поверхности.

В случае произвольной поверхности, окружающей n зарядов, поток напряженности через нее равен сумме потоков, создаваемых каждым из зарядов:

.

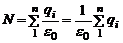Таким образом, поток напряженности, пронизывающий любую замкнутую поверхность, окружающую электрические заряды, пропорционален алгебраической сумме окруженных зарядов.

Это положение называется теоремой Остроградского-Гаусса.