Работа силы в некоторых случаях

1. Сила постоянна по величине. Точка или тело движется прямолинейно.

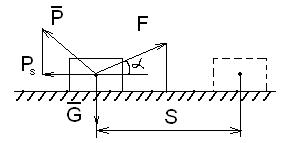
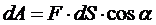
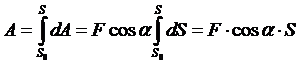
Знаки работы:

при α < 90°; A > 0

при α = 90°; A = 0

при 90° < α < 180°; A < 0

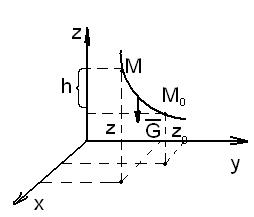
2. 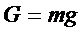Работа силы тяжести.

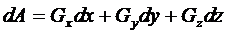
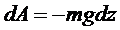
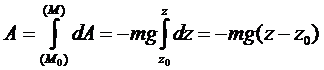
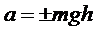
3. Работа силы при вращательном движении тела вокруг неподвижной оси.

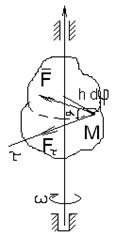
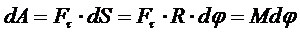
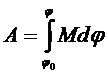
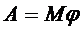Если М = const, то

4. Работа силы упругости пружины.

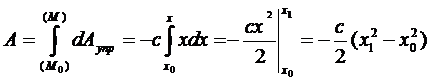
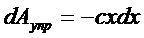
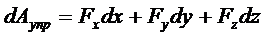
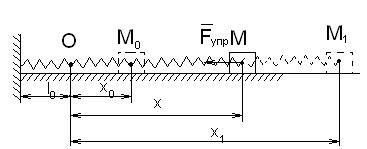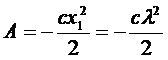
Если x₀ = 0, то

Единицей измерения работы в СИ является –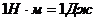

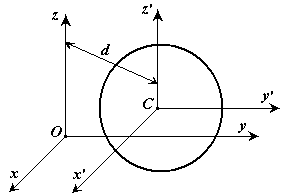
Установим зависимость между моментами инерции относительно параллельных осей, одна из которых проходит через центр масс.

Теорема о моментах инерции относительно параллельных осей. (Теорема Штейнера)

Момент инерции системы относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр масс, плюс произведение массы системы на квадрат расстояния между этими осями.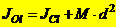

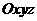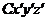Доказательство: Пусть имеется две декартовы системы координат и , оси которых параллельны. Начало системы 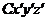находится в центре масс системы. Докажем теорему для осе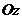й и .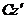

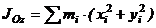
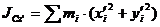
Координаты связаны между собой соотношениями:

, ,

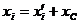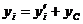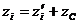
Работа силы. Мощность.

Одна из основных характеристик силы, оценивающих действие силы на тело при некотором его перемещении.

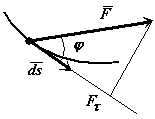Элементарная работа силы скалярная величина равная произведению элементарного перемещения на проекцию силы на это перемещение.

. ,

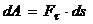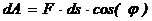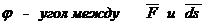
Элементарная работа силы равна скалярному произведению силы на элементарное перемещение или на дифференциал радиуса вектора точки приложения силы.

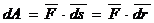
Элементарная работа силы равна скалярному произведению элементарного импульса силы на скорость точки.

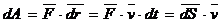
Мощностью силы называется величина, определяющая работу, совершаемую силой в единицу времени. В общем случае мощность равна первой производной по времени от работы.

,

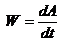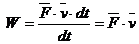
Мощность равна скалярному произведению силы на скорость.

Единицей измерения мощности в СИ является –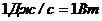

В технике за единицу силы принимается .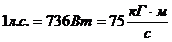

Теорема об изменении кинетической энергии системы.

Эта теорема существует в двух формах.

Теорема. Дифференциал кинетической энергии системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему.

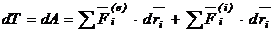
Теорема. Изменение кинетической энергии системы при ее перемещении из одного положения в другое равно сумме работ всех внешних и внутренних сил, действующих на систему, на соответствующих перемещениях точек системы при том же перемещении системы..

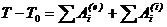
Теорема Кенига. Кинетическая энергия системы в абсолютном движении складывается из кинетической энергии центра масс, если в нем сосредоточить всю массу системы, и кинетической энергии системы при ее движении относительно центра масс.

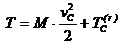
Вычисление обобщённых сил

Если система имеет n степеней свободы, то у неё n обобщённых координат, независимых друг от друга (q₁, q₂, …, q_n) и n возможных перемещений (δq₁, δq₂, …, δq_n). Сумма элементарных работ, приложенных к системе сил, на возможные перемещения системы равна

.

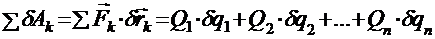Обобщёнными силами называются коэффициенты, стоящие перед соответственными возможными перемещениями. Так как обобщённые координаты не зависят друг от друга, то для определения обобщённой силы системе необходимо сообщить возможные перемещения, соответствующие координатам, а все остальные возможные перемещения принять за нуль, то есть для определения Q₁ необходимо, чтобы δq₁ ≠ 0, δq₂ = 0, δq₃ = 0, …, δq_n = 0, тогда

.

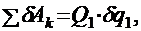
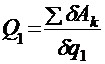Размерность обобщённых сил зависит от размерности обобщённых координат: если q_j = x (м), то Q_j – сила (Н); если q_j = φ (рад), то Q_j – момент (Н∙м).