Математическая модель описания процессов распространения сигналов по направляющим системам в широком диапазоне частот

Для создания математической модели используют законы, которые связывают параметры среды (s, e и m) с напряжённостью электромагнитного поля.

Е [В/М] - напряжённость электрического поля ,

Н [А/М] - напряжённость магнитного поля .

Используют законы Максвелла (1-й и 2-й).

В технике информации законы Максвелла записываются в дифференциальной форме, используя оператор «ротор» - это дифференциальный оператор, который отражает степень кривизны векторов электромагнитного поля.

1-й закон Максвелла:

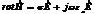
где:

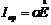- ток проводимости;

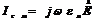- ток смещения.

Ток проводимости существует в металлах

Ток смещения существует в диэлектриках , пропорционален частоте, обычно ток смещения учитывается на ВЧ, от 1 МГц.

2-й закон Максвелла:

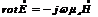
Можно создать 5 режимов передачи по направляющим системам:

1) Статический режим - наличие неподвижных зарядов. Правые части 1 и 2 равны 0.

2) Стационарный режим - характерен для проводников т.к. существует ток проводимости , второе слагаемое из 1 и правая часть из 2 равны 0 - характеризует распространение тока по проводникам .

3) Квазистационарный режим -первым слагаемым из 1 существует , токами смещения пренебрегают , но магнитные поля существуют как в проводнике так и в диэлектрике . Этот режим справедлив до 10 МГц

4) Волновой режим передачи - пренебрегаем током проводимости , т.к.. этот режим описывает распространение сигналов по диэлектрику . Для описания распространения электромагнитных волн от антенн , в радиосвязи .

5) Электромагнитный режим передачи - используют полное уравнение Максвелла . Распространение сигналов по волноводам.

Представление направляющей системы в квазистационарном режиме

Создание физической модели направляющей системы и математической системы этой системы в квазистационарном режиме.

Пренебрежение вторым слагаемым из 1 - позволяет использовать законы ТЛЭЦ.

Мы можем представить линию в виде наборов ЧП, причём каждая элементарная длина линии представляется в виде отдельного ЧП, который содержит продольные и поперечные параметры:

Продольные параметры : R [Ом/км]

L [Гн/км]

Поперечные параметры : G [См/км]

C [Ф/км] . Где G и R не связанные величины .

Лекция № 3

Тема: Продолжение (Представление линии в квазистационарном ре­жиме)

Составим схему замещения (физическая модель) в квазистационарном режиме.

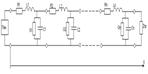
Задача: определить изменение тока генератора (передатчика) в зависимости от параметров линии и её длины.

Решать необходимо при проектировании усилительных пунктов по магистрали.

Для определения I_X и U_X.

Составим математическую модель, используя систему дифференциальных уравнений, которая связывает на­пряжение и ток в линии с её первичными параметрами.

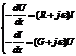Система (1)

Уравнения системы (1) получили название телеграфных уравнений.

Рассмотрим первое уравнение из системы (1).

Оно отражает падение напряжения на продольных параметрах линии от тока, те­кущего вдоль линии.

2-е уравнение из системы (1) отражает ток утечки и говорит, что ток утечки зависит от потенциала линии и поперечных параметров, т.е. проводимости изоляции и ём­кости.

Необходимо перейти от Д.У. к алгебраическим уравнениям - для выполнения инженерных расчетов.

Вводятся понятия:

· Z_В - волновое сопротивление;

· g - коэффициент километрического затухания. (g)

При эксплуатации линейного сооружения стремятся создать режим согласованных нагрузок, который предполагает равенство волнового сопротивления линии (Zв), внутреннего сопротивления генератора (Zг) и сопротивление приемника (Zпр).

В этом режиме будут отсутствовать отражённые волны.

Тогда для этого режима решение будет выглядеть следующим образом:

Ток и напряжение меняется по экспоненте в зависимости от длины линии и g.

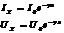Система (2)

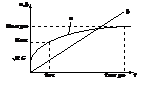
Рис.2

· ¡2>¡1-затухание больше;

· ¡3<¡1-затухание меньше.

Сопротивление передатчика полностью определяется g, а g зависит от первичных параметров линии.

Затухание g связывает все 4 параметра:

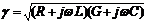формула 1

Из этой формулы следует, что g:

· Частотно-зависимый параметр · Этот параметр комплексный, т.е. существует реальная и мнимая части, часто для практических инженерных расчетов выделяют: 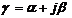, где a -определяет степень затухания амплитуды сигнала; b-определяет изменение фазы сигнала.

Частотные зависимости g(a и b) отличаются.

ОТС - оперативно-технологическая связь

МАГ, ДОР - магистральная, дорожная связь

Рассмотрим: как будет изменяться расстояние м/у усилителями в НЧ области, в которой работают оперативно-технологические цепи отделенческих видов связи и ВЧ области, в которой работают каналы магистральной и дорожной связи.

Частотный диапазон:

· Магистральный и дорожный вид связи в зависимости от аппаратуры передачи вплоть до 252 кГц;

· Оперативно-технологическая связь до 4 кГц.

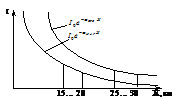
Рис 4

Чем выше частота передатчика тем меньше расстояние между усилительными пунктами, но большее число каналов мы можем организовать.

Зная параметры линии мы можем определить расстояние между усилительными пунктами.

Кроме частотной зависимости g зависит от параметров линии, чем больше продольные параметры линейного сооружения, тем меньше частотный диапазон и больше затухание.

Примером тому служат В.Л., в особенности со стальными цепями (примерно 3 канала), с медными или биметаллическими цепями (максимум 12 каналов) - ограничено 150 КГц.

Если увеличить частоту - резкое увеличение затухания.

Волновое сопротивление Zв

Связь между Zв и первичными параметрами:

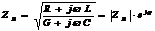
Zв зависит:

· От всех четырёх параметров;

· Частотно-зависимый параметр;

· Комплексный параметр.

Рассмотрим частотную зависимость модуля Zв и угла сопротивления j.

Примем крайние значения:

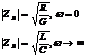
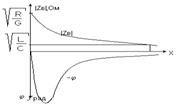
Замечания:

1) В области ВЧ волновое сопротивление имеет чисто активный чарактер,часто это показывается в параметрах кабеля РК-50, РК-75, где цифра означает волновое сопротивление кабеля в омах;

2) Т.к. волновое сопротивление линии на ВЧ является чисто активным параметром, то легко согласовать параметры линейного сооружения с внутренним сопротивлением передатчика и приемника ( с их параметрами ) для оптимальной работы линии. В противном случае возникает режим несогласованности нагрузки.