Векторная диаграмма идеального трансформатора

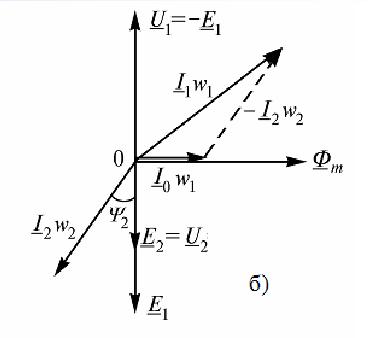
Уравнения линейного трансформатора.

Пусть i1, i2 — мгновенные значения тока в первичной и вторичной обмотке соответственно, u1 — мгновенное напряжение на первичной обмотке, RH — сопротивление нагрузки. Тогда

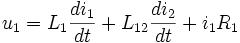
Здесь L1, R1— индуктивность и активное сопротивление первичной обмотки, L2, R2— то же самое для вторичной обмотки, L12— взаимная индуктивность обмоток. Если магнитный поток первичной обмотки полностью пронизывает вторичную, то есть если отсутствует поле рассеяния, то 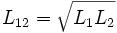. Индуктивности обмоток в первом приближении пропорциональны квадрату количества витков в них.

Мы получили систему линейных дифференциальных уравнений для токов в обмотках. Можно преобразовать эти дифференциальные уравнения в обычные алгебраические, если воспользоваться методом комплексных амплитуд.

Для этого рассмотрим отклик системы на синусоидальный сигнал u1=U1 e-jω t (ω=2π f, где f — частота сигнала, j — мнимая единица). Тогда i1=I1 e^-jω t и т. д., сокращая экспоненциальные множители получим

U1=-jωL1 I1 -jωL12 I2+I1 R1

-jωL2 I2 -jω L12 I1+I2 R2 =-I2 Zн

Метод комплексных амплитуд позволяет исследовать не только чисто активную, но и произвольную нагрузку, при этом достаточно заменить сопротивление нагрузки Rн её импедансом Zн. Из полученных линейных уравнений можно легко выразить ток через нагрузку, воспользовавшись законом Ома— напряжение на нагрузке, и т. п.

Т-образная Схема замещения трансформатора

Составление схемы замещения. Систему уравнений (1.20) – (1.22), описывающую электромагнитные процессы в трансформаторе, можно свести к одному уравнению, если учесть, что 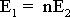, и положить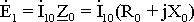

При этом параметры R0 и X0 следует выбирать так, чтобы в режиме холостого хода, когда ЭДС E1 практически равна номинальному напряжению U1, ток

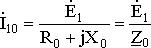
по модулю равнялся бы действующему значению тока холостого хода, а мощность – мощности, забираемой трансформатором из сети при холостом ходе.Решим систему уравнений (1.20) – (1.22) относительно первичного тока

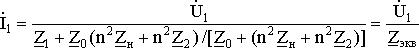
В соответствии с уравнением (1.28) трансформатор можно заменить электрической схемой, по которой можно определить токи Í1 и Í2, мощность P1, забираемую из сети, мощность ΔP потерь и т.д. Такую электрическую схему называют схемой замещения трансформатора

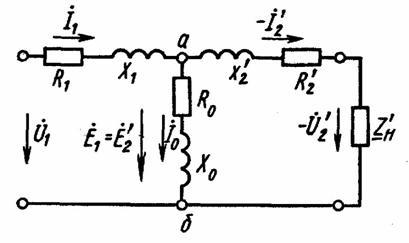
Эквивалентное сопротивление этой схемы

где: , , ,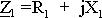

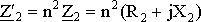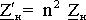
Потери в трансформаторах

Потери энергии в стали сердечника трансформатора складываются из потерь на гистерезис и потерь на вихревые токи.

Потери на гистерезис можно сравнить с потерями на трение — под воздействием переменного магнитного поля магнитные домены, подобные миниатюрным магнитам, должны изменять свое направление, преодолевая силы внутреннего сцепления в ферромагнетике. Чем тверже ферромагнетик, тем больше потери на гистерезис. Эти потери за один цикл перемагничивания пропорциональны площади петли гистерезиса материала. В общем виде мощность этих потерь выражается формулой

P1 = Kг f BmnG

где Kг — гистерезисный коэффициент, значение которого зависит от сорта стали; f —частота переменного тока, Вт — амплитуда магнитной индукции; G — масса сердечника. Значение показателя степени можно считать п = 2 при Вт > 1 Т и п = 1,6 при Вт < 1 Т.

Потери на вихревые токи определяются ориентировочно на основании приближенного расчета мощности, развиваемой токами. Эдс, индуктируемую в стали переменным магнитным потоком, можно выразить через трансформаторную эдс, так как масса металла подобна некоторому короткозамкнутому витку, следовательно,

EB= 4,44 fФm =4,44 f SB Bm

здесь SB —площадь, охватываемая этим витком и пронизываемая потоком. Чем эти площадь больше, чем больше вихревые токи, создаваемые индуктируемой эдс. Мощность потерь в контуре подобного вихревого тока

PB. кон = EB2g

где g — активная проводимость этого контура. Расчет такой мощности представляет собой существенные трудности, но для качественной оценки потерь существенно лишь то, что проводимость g пропорциональна удельной проводимости у стали. Таким образом, мощность потерь на вихревые токи можно выразить следующим образом:

PB = KB f 2Bm2g G,

где KB — коэффициент вихревых токов, значение которого зависит от сорта стали и толщины листа стали.

Амплитуда магнитной индукции Вт в современных трансформаторах, как и в сердечниках большинства машин переменного тока, больше 1 Тл. Следовательно, как потери на вихревые токи, так и потери на гистерезис в них пропорциональны В2т и (SB Bm)2=Фm Таким образом, суммарные потери энергии в стали сердечника пропорциональны квадрату магнитного потока, а потери в проводниках обмотки — квадрату тока.

Практически при расчетах определяются суммарные потери в стали с помощью справочных таблиц. Например, потери в стали Э41 — 0,35 (при толщине листа 0,35 мм) при амплитуде индукции Вт = 1 Тл составляют 1,3 Вт/кг, а при Вт = 1,5 Тл они будут уже 3 Вт/кг.