Регулировочных характеристик
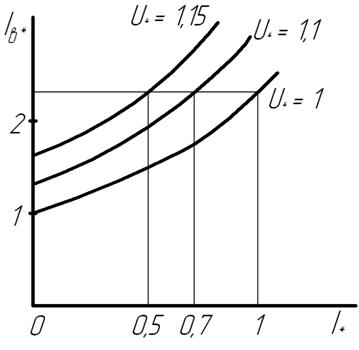
Рис. 12. Регулировочные характеристики
163. Внешняя характеристика U* = f(I*).
Внешнюю характеристику можно построить, используя семейство регулировочных характеристик (рис. 12). Из точки, соответствующей U* = 1 и I* =1, проведем прямую параллельно оси абсцисс. Точки пересечения этой прямой с регулировочными характеристиками дадут значения тока I* при U* = 1,1 и U* = 1,15. Значение U* при I* =0 получим по характеристике холостого хода для Iвн*. Данные расчета сведены в табл. 6.
Таблица 6
| I* | 0,5 | 0,7 | ||
| U* | 1,26 | 1,15 | 1,1 |
По данным табл. 6 на рис. 13 построена внешняя характеристика.
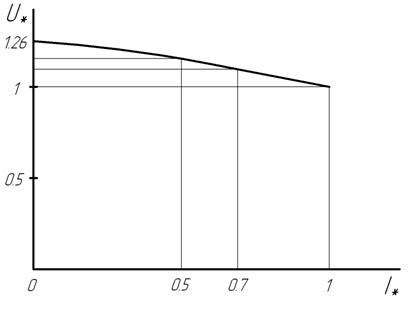
Рис. 13. Внешняя характеристика
164. U-образная характеристика I*=f(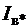 
).
При построении U-образной характеристики должно быть обеспечено выполнение условий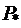 
=const и 
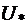= const. Принимая во внимание, что 
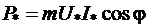, можно отметить, что активная составляющая тока якоря 
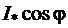также постоянна.
Для U-образной характеристики при U*=Uн* и Р*=Р*н=cosφ=0,8 активная составляющая тока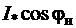 
равна 0,8. Для характеристик при 
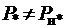, например при 
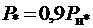, активная составляющая 
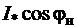= 0,9·0,8 =0,72 и т.д.
U-образную характеристику для случая Р*=0,8; U* = Uн* строим следующим образом. Откладываем по оси абсцисс в масштабе вектор напряжения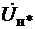 
. С ним совпадает по направлению вектор активного тока Iн*cosφн (рис. 14). Затем задаемся несколькими значениями тока I*, например двумя I(1)* =1, I(2)* =0,9 для индуктивной нагрузки (φ>0), одним для активной нагрузки I(3)* = =Iн*cosφн и одним I(4)* =0,88 для емкостной нагрузки (φ<0), и размещаем их, как показано на рис. 14. Определяем для этих токов углы φ.
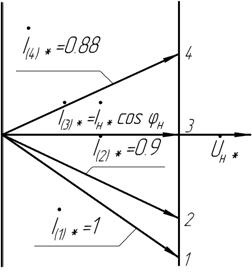
Рис. 14. Векторные диаграммы
(к построению U-образной характеристики)
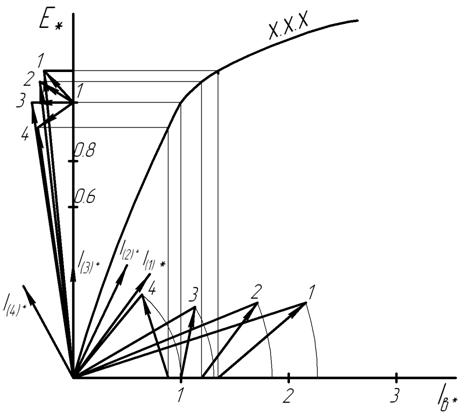
Рис. 15. Диаграмма Потье (к построению U-образной характеристики)
Для каждого значения I(1,2,3,4)* и φ(1,2,3,4) строим диаграмму Потье, как это делалось при построении регулировочных характеристик (рис. 15).
Данные расчёта сводим в табл. 7
Таблица 7
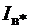 | 1,32 | 1,85 | 2,25 | |
| I* | 0,88 | 0,8 | 0,9 | 1,0 |
По данным табл. 7 строим U-образную характеристику (рис. 16).
U-образная характеристика I*=f( 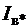) может быть построена без учёта насыщения магнитопровода. При этом будем считать синхронную машину неявнополюсной (аналогично допущению при построении диаграммы Потье) с синхронным индуктивным сопротивлением 
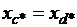. Учтём ранее указанное соотношение 
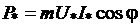, откуда следует постоянство активной составляющей тока якоря 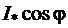. С другой стороны, электромагнитная мощность неявнополюсной машины 
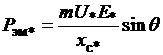. Пренебрегая незначительной разницей между его выходной электрической и электромагнитной мощностями, будем считать, что выполнение условия постоянства мощности, необходимого для построения U-образной характеристики, обеспечивается также постоянством произведения 
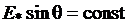(т.к. остальные параметры формулы для определения 
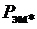являются постоянными). Следствием полученных условий построения U-образной характеристики, а именно: 
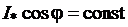и 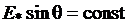, является то, что конец вектора тока якоря при изменении угла φ перемещается вдоль линии тока I, а конец вектора ЭДС возбуждения – вдоль линии ЭДС E (рис.17). Промежуточные относительные значения тока якоря и возбуждения могут быть получены пропорциональным пересчётом соответствующих длин векторов тока якоря и ЭДС возбуждения по отношению к указанным величинам для базовой векторной диаграммы для номинального режима (на рис.17 базовая диаграмма 1 выделена утолщёнными линиями). С учётом допущения о неучёте насыщения можно считать 
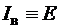. В качестве примера на рис. 17 показано построение диаграмм для отстающего (1), активного (2) и опережающего (3) тока для номинальной мощности, а также для активного (2’) тока при 50 % процентной мощности.
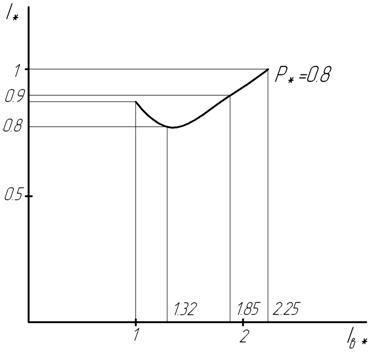
Рис. 16. U-образная характеристика
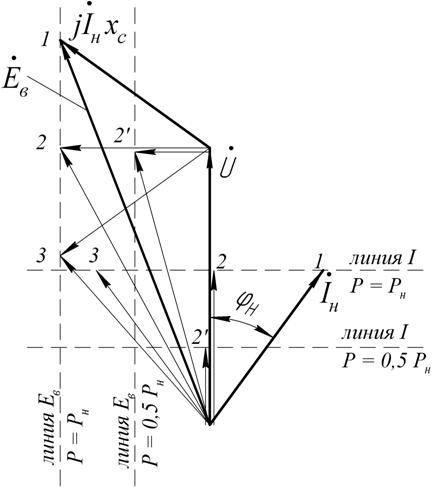
Рис. 17. Векторная диаграмма (к построению U-образной характеристики без учёта насыщения стали)
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Проектирование электрических машин: Учеб. пособие для вузов: В 2 кн./ И.П. Копылов, Б.К. Клоков, В.П.Морозкин и др.; Под. ред. И.П. Копылова.– 2-е изд., перераб. и доп. М.:Энергоатомиздат, 1993. Кн. 2. 384 с.
2. Буханцов Е.И. Методические указания к курсовому проекту по электрическим машинам. Синхронные генераторы/ НПИ. Новочеркасск, 1984. 48 с.
3. Буханцов Е.И. Методические указания. Пример расчёта синхронного генератора/ НПИ. Новочеркасск, 1985. 40 с.
4. Электротехнический справочник/ Под ред. П.Г. Грудинского, Г.Н. Петрова, М.И. Соколова, А.М. Федосеева, М.Г. Чиликина, И.В. Антика. Изд. 5–е. М.: Энергия, 1974. Т. 1. 775 с.
5. Видеман Е., Келлепбергер В. Конструкции электрических машин/Сокр. пер. с нем.; Под ред. Б.Н. Красовского. Л.: Энергия, 1972.; 520 с.
6. Виноградов Н.В. Производство электрических машин. М.: Энергия, 1970. 288 с.
7. СТП–40.459–007–82. Стандарт предприятия. Текстовые документы в учебном процессе. Общие требования/ НПИ. Новочеркасск, 36 с.
Учебное издание
Пахомин Сергей Александрович