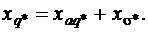Определение МДС реакции якоря

При определении МДС обмотки возбуждения, необходимой для создания нужного потока при нагрузке, необходимо учитывать влияние реакции якоря. Амплитуда первой гармоники МДС рeaкции якоря при токе фазы I_ф

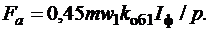
МДС реакции якоря F_a обычно разлагают на две составляющие: продольную F_d=F_a sinψ и поперечную F_q=F_a cosψ , где ψ – угол между векторами тока I_ф и ЭДС холостого хода Е_о. Одинаковые МДС обмотки возбуждения и якоря создают различные потоки, поэтому одну из МДС необходимо привести к другой. Так как при расчетах используют характеристику холостого хода E=f(I_во), то целесообразно МДС якоря привести к МДС обмотки возбуждения. При переходе от F_d и F_q к эквивалентным F_ad и F_aq используют коэффициенты k_ad и k_aq:

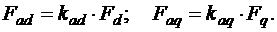
Коэффициенты k_ad и k_aq , зависящие от отношений b_p/τ =α и δ/τ, находят по рис. 8.1.

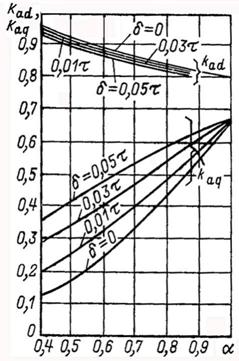
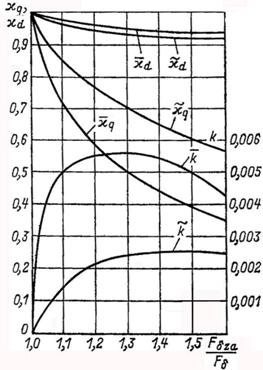
Рис. 8.1 Рис. 8.2

Приближенно учет насыщения осуществляют следующим образом. Определяют коэффициенты χ_q и χ_d в функции отношения F_δZa/F_δ (рис. 8.2), на которые умножают МДС F_ad и F_aq,чтобы получить их насыщенные значения F'_ad и F'_aq.

Для компенсации размагничивающего действия поперечной реакции якоря при насыщении магнитопровода увеличивают МДС обмотки возбуждения на некоторую величину F_qd . В случае δ_м/δ=1,5

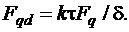
Определение параметров обмотки статора

Для установившегося режима работы

Для построения диаграмм и расчета характеристик необходимо знать параметры обмотки статора.

Активное сопротивление обмотки статора, Ом,

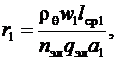
где ρ_θ – удельное сопротивление медного проводника обмотки, равное

10^-6/57, 10^-6/47 и 10^-6/41 Ом·м соответственно при температурах 20, 75, 115 °С; q_эл·n_эл – сечение эффективного проводника, м²; 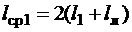– средняя длина витка обмотки статора, м.

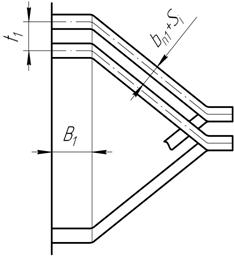В случае выполнения обмотки из прямоугольного провода длина лобовой части

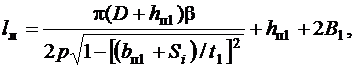
где β=y₁/τ – относительное укорочение шага обмотки статора; S_i – допустимое расстояние между соседними катушками в лобовой части; В₁ – вылет прямолинейной части катушек из паза (рис. 9.1). Параметры S_i и В₁ в зависимости Рис. 9.1

от номинального напряжения определяются по табл. 9.1.

Активное сопротивление фазы в относительных единицах

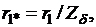
где 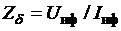– базовое сопротивление.

Индуктивное сопротивление рассеяния фазы статора

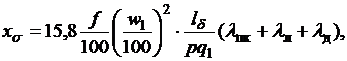
где λ_пк, λ_л, λ_д – коэффициенты удельной (на единицу длины) магнитной проводимости пазового, лобового и дифференциального рассеяния.

Таблица 9.1

UH, В	Si, м	B1, м
≤ 660	0,0035	0,025
До 3300	0,005 – 0,006	0,035 – 0,04
До 6600	0,006 – 0,007	0,04 – 0,05
≥ 10000	0,007 – 0,008	0,06 – 0,065

Коэффициент

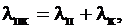
где 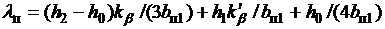– проводимость между стенками паза, а 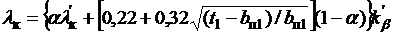– проводимость по коронкам зубцов. Здесь h₀, h₁, h₂ – высоты частей паза, зависящие от площади паза, занятой медью, и определяемые внешними кромками крайних проводников сторон катушек без учета изоляции (рис. 9.2); 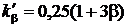при 2/3≤β<1, 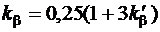– коэффициенты, зависящие от укорочения обмотки; α=b_p/τ – коэффициент полюсного перекрытия; λ'_к – по рис. 9.3.

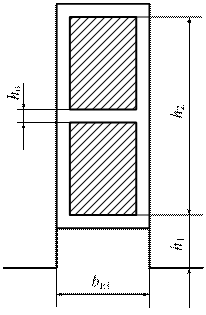
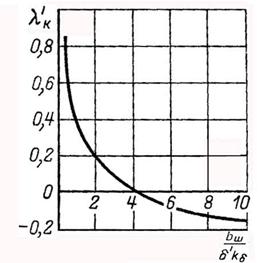
Рис. 9.2 Рис. 9.3

Коэффициент проводимости лобового рассеяния

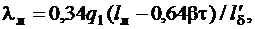
где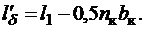

Коэффициент проводимости дифференциального рассеяния

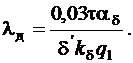
Индуктивное сопротивление рассеяния в относительных единицах

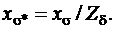
Индуктивное сопротивление продольной реакции якоря в относительных единицах

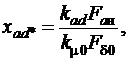
где 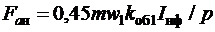– МДС статора при номинальном токе;

F_δ0 – магнитное напряжение воздушного зазора при E=U_нф; 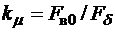– коэффициент, который находят из расчета магнитной цепи для точки, соответствующей Е = 0,5U_нф.

Индуктивное сопротивление поперечной реакции якоря в относительных единицах

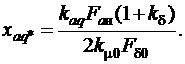
Синхронное индуктивное сопротивление по поперечной оси