Лекция 11. Физика атомов и молекул

11.1. Модель атома Резерфорда

До 1911 г. не было правильных представлений о строении атома. В 1911 г. Резерфорд и его сотрудники исследовали рассеяние a-частиц при прохождении через тонкие металлические слои (a-частицы испускают радиоактивные элементы. Они представляют собой ядра атомов гелия с зарядом 2е и массой, приблизительно в 4 раза большей, чем масса атома водорода. Скорость их достигает » 10⁷ м/с). Было установлено, что при облучении листка золота толщиной 6 мкм значительное отклонение от первоначального направления движения испытывала лишь одна из 8000 a-частиц. Результат получился таким же неожиданным для того времени, как если бы при обстреле кирпичами кирпичной стены толщиной в несколько тысяч кирпичей почти все кирпичи проходили бы сквозь стену и лишь некоторые отскакивали бы от стены.

На основании своих исследований Резерфорд предложил ядерную модель атома. Согласно этой модели атом состоит из положительного ядра, имеющего заряд Zе (Z - порядковый номер элемента в таблице Менделеева, е - элементарный заряд), размер 10^-5 -10^-4 А (1А= 10^-10 м) и массу практически равную массе атома. Вокруг ядра по замкнутым орбитам движутся электроны, образуя электронную оболочку атома. Так как атомы нейтральны, то вокруг ядра должно вращаться Z электронов, суммарный заряд которых - Zе. Размеры атома определяются размерами

внешних орбит электронов и составляют порядка единиц А.

Масса электронов составляет очень малую долю массы ядра (для водорода 0,054%, для остальных элементов менее 0,03%). Понятие “размер электрона” не удается сформулировать непротиворечиво, хотя r_o » 10^-3 А называют классическим радиусом электрона.

Итак, ядро атома занимает ничтожную часть объема атома и в нем сосредоточена практически вся (» 99,95%) масса атома. Если бы ядра атомов располагались вплотную друг к другу, то земной шар имел бы радиус » 200 м а не » 6400 км (плотность вещества атомных ядер » 1,8×10¹⁷ кг/м³). Поэтому с точки зрения атомистических представлений всякую среду следует рассматривать как вакуум, в который вкраплены атомные ядра и электроны (или по другому - как вакуум, слегка испорченный вкрапленными в него атомными ядрами и электронами).

Результаты опытов по рассеиванию a-частиц свидетельствуют в пользу ядерной модели атома. Однако ядерная модель оказалась в противоречии с законами классической механики и электродинамики. Покажем это.

Предположим, что электрон движется вокруг ядра по круговой орбите радиуса r. При этом кулоновская сила взаимодействия между электроном и ядром сообщает электрону нормальное (центростремительное) ускорение, определяемое из второго закона Ньютона.

. (1)

При r = 1А из (1) находим, что а_n » 10²² м/с². Согласно классической электродинамике ускоренно движущиеся электроны должны излучать электромагнитные волны (см. параграф 2.4.) и вследствие этого терять энергию. В результате электроны будут приближаться к ядру и в конце концов упадут на него, что противоречит действительности.

Выход из создавшего тупика был найден в 1913 г. Нильсом Бором, который сформулировал 2 постулата, противоречащие классическим представлениям.

11.2. Постулаты Бора

1. Первый постулат заключается в следующем:

Существуют только некоторые стационарные состояния атома, находясь в которых он не излучает энергию. Этим стационарным состояниям соответствуют вполне определенные (стационарные) орбиты, по которым движется электроны. При движении по стационарным орбитам электроны, несмотря на наличие у них ускорения, не излучают электромагнитных волн.

В стационарном состоянии атома электрон должен иметь дискретные (квантованные) значения момента импульса

L_n = mrv = n 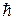, n = 1, 2, ... (2)

Здесь m,v- масса и скорость электрона, r - радиус его орбиты. С учетом (1) и (2) находим радиусы стационарных орбит электронов

. (3)

Для атома водорода (Z=1) радиус первой орбиты электрона при n = 1, называемый первым боровским радиусом (а), равен

r₁ = a = 0,528 А. (4)

внутренняя энергия атома слагается из кинетической энергии электрона (Т = mv²/2) и потенциальной энергии взаимодействия электрона с ядром (U =-Ze²/(4pe₀r)),

(5)

при выводе формулы (5) учли формулу (1). Подставляя в (5) квантовые радиусы орбит электронов (3), получим, что энергия атома (которая равна энергии электрона, так как ядро атома неподвижно) может принимать только следующие дозволенные дискретные (квантовые) значения

(6)

или

где знак минус означает, что электрон находится в связанном состоянии. (В атомной физике энергия измеряется в электронвольтах, 1 эВ = 1,6×10^-19Дж).

2. Второй постулат устанавливает :

При переходе атома (электрона) из одного стационарного состояния в другое испускается или поглощается один фотон с энергией

, (7)

где Е_n, Е_m - энергии атома (электрона) в стационарных состояниях n и m, которые определяются согласно (6).

Исходя из своих постулатов Бор создал полуклассическую теорию простейшего водородоподобного атома и объяснил линейчатый спектр атом водорода. К водородоподобным атомам относятся атом водорода (z=1), ион гелия Не⁺ (z=2), ион лития Li⁺⁺ (Z=3) и др. Для них характерно, что вокруг ядра с зарядом = Ze вращается только один электрон.

11.3. Линейчатый спектр атома водорода

Спектр излучения атомарного водорода состоит из отдельных спектральных линий, которые располагаются в определенном порядке. В 1885 г. Бальмер установил, что длины волн (или частоты) этих линий могут быть представлены формулой. Действительно, из (7) с учетом (6) для водорода (Z = 1), следует, что

, (8)

где R = 2,07× 10¹⁶ с ^-1 - постоянная Ридберга

Учитывая, что 1/l = v/с = w/2pс и используя (8), найдем

, (9)

где R =1,0974×10⁷ м^-1 - называется также постоянной Ридберга.

На рис. 1 изображена схема энергeтических уровней атома водорода, расчитанных согласно (6) при z=1.

Е_n, эВ

0 n = ¥

-0,85

n = 4

n = 3

-1,51

СП

	-3,4
		n = 2

СБ

	-13,6

СЛ

При переходе электрона с более высоких энергетических уровней на уровень n = 1 возникает ультрофиолетовое излучение или излучение серии Лаймана (СЛ). Когда электроны переходя на уровень n = 2 возникает видимое излучение или излучение серии Бальмера (СБ). При переходе электронов с более высоких уровней на уровень n = 3 возникает инфракрасное излучение, или излучение серии Пашена (СП) и т.д.

Частоты или длины волн, возникающего при этом излучения, определяются по формулам (8) или (9) при m=1 - для серии Лаймана, при m=2 - для серии Бальмера и при m = 3 - для серии Пашена. Энергия фотонов определяется по формуле (7), которую с учетом (6) можно привести для водородоподобных атомов к виду :

эВ (10)

Теория Бора сыграла огромную роль в создании атомной физики. В период ее развития (1913 - 1925 г.) были сделаны важные открытия , например, в области атомной спектроскопии. Однако в теории Бора обнаружились существенные недостатки, например, с ее помощью невозможно создать теорию более сложных, чем атом водорода, атомов. Поэтому становилось очевидным, что теория Бора представляет собой переходной этап на пути создания последовательной теории атомных и ядерных явлений. Такой последовательной теорией явилась квантовая (волновая) механика.

11.4 Атом водорода согласно квантовой механики. Квантовые числа электрона в атоме

Результаты полученные согласно теории Бора в решении задачи об энергетических уровнях электрона в водородоподобных атомах, получены в квантовой механике без привлечения постулатов Бора. Покажем это.

Состояние электрона в водородоподобном атоме описывается некоторой волновой функцией y, удовлетворяющей стационарному уравнению Шредингера [см.(9.22)]. Учитывая, что потенциальная энергия электрона

(11)

где r - расстояние между электроном и ядром, получим уравнение Шредингера в виде

(12)

Целесообразно воспользоваться сферической системой координат r, q, j и искать решение этого уравнения в виде следующих собственных функций

(13)

где n, l, m - целочисленные параметры собственных функций. При этом n - называют главным квантовым числом, l - орбитальным (азимутальным) и m - магнитным квантовым числом.

Доказывается, что уравнение (12) имеет решение только при дискретных отрицательных значениях энергии

(14)

где n = 1, 2, 3,... главные квантовые числа.

Сравнение с выражением (6) показывает, что квантовая механика приводит к таким же значениям энергии, какие получились и в теории Бора. Однако в квантовой механике эти значения получаются как следствие основных положений этой науки.

Подставив в (14 ) Z=1 и приняв n = 1, получим значение энергии основного состояния (т.е. состояния с наименьшей энергией) атома водорода

эВ. (15)

Из решения (13) уравнения Шредингера (12) также следует, что момент импульса электрона в атоме квантуется по формуле

(16)

где l= 0, 1, 2, ... (n-1), орбитальное (азимутальное) квантовое число.

Проекция момента импульса L электрона на направление Z магнитного поля может принимать лишь целочисленные значения, кратные (пространственное квантование) т.е.

(17)

m - называют магнитным квантовым числом. При данном магнитное квантовое число может принимать различных значений.

Lz

Опыт Штерна и Герлаха, а также более ранние эксперименты привели Уленбека и Гаудсмита к гипотезе существования у электрона собственного момента импульса, который был назван спин (spin - верчение).

Lz         -

l=1 l=2

Рис. 2

Первоначально предполагалось, что спин обусловлен вращением электрона вокруг своей оси. Позднее было показано, что спин имеет квантовую природу. Спин следует считать внутренним свойством, присущим электрону, подобно тому как ему присущ и заряд и масса.

Собственный момент импульса электрона L_S (спин) выражается через спиновое квантовое число s равное 1/2, т.е. спин квантуется по закону

.

Проекция спина на заданное направление z может принимать два квантованных значения

,

где m_s = ± s = ± 1/2 называют магнитным спиновым квантовым числом или просто спиновым квантовым числом, т.е. также как и s.

11.5. Принцип Паули

Итак, состояние каждого электрона в атоме характеризуется четырьмя квантовыми числами:

1. Главное квантовое число n (n = 1, 2 ... ¥).

2. Орбитальное (азимутальное) квантовое число l (l = 0, 1, 2, ... n-1)

3. Магнитное квантовое число m (m = 0, ± 1, ± 2, ± ... ± l)

4. Спиновое квантовое число m_s (m_s = ± 1/2 ).

Для одного фиксированного значения главного квантового числа n существует 2n² различных квантовых состояний электрона.

Один из законов квантовой механики, называемый принципом Паули, утверждает:

В одном и том же атоме не может быть двух электронов, обладающих одинаковым набором квантовых чисел, (т.е. не может быть двух электронов в одинаковом состоянии).

Принцип Паули дает объяснение периодической повторяемости свойств атома, т.е. периодической системе элементов Менделеева.