Лекция 8. Квантовые свойства электромагнитного излучения
1. Фотоны, энергия, масса и импульс фотона
Чтобы объяснить распределение энергии в спектре теплового излучения Планк допустил, что электромагнитные волны испускаются порциями (квантами). Эйнштейн в 1905 г. пришел к выводу, что излучение не только испускается, но и распространяется и поглощается в виде квантов. Этот вывод позволил объяснить все экспериментальные факты (фотоэффект, эффект Комптона, и др.), которые не могла объяснить классическая электродинамика, исходившая из волновых представлений о свойствах излучения.
Таким образом, распространение света следует рассматривать не как непрерывный волновой процесс, а как поток локализованных в пространстве дискретных частиц, движущихся со скоростью с распространения света в вакууме. Впоследствии (в 1926 г.) эти частицы получили название фотонов. Фотоны обладают всеми свойствами частицы (корпускулы).
1. Энергия фотона
e=hv= 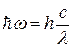 , (1)
, (1)
где h=6.6×10-34 Дж×с - постоянная Планка, 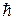 =h/2p=1.055×10-34 Дж×с также постоянная Планка, w=2pv - круговая частота.
=h/2p=1.055×10-34 Дж×с также постоянная Планка, w=2pv - круговая частота.
В механике есть имеющая размерность "энергия´время" величина, которая называется действием. Потому постоянную Планка иногда называют квантом действия. Размерность 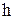 , совпадает, например, с размерностью момента импульса (L=r mv).
, совпадает, например, с размерностью момента импульса (L=r mv).
Как следует из (1) энергия фотона увеличивается с ростом частоты (или с уменьшением длины волны), и, например, фотон фиолетового света (l=0.38 мкм) имеет большую энергию, чем фотон красного света (l=0.77 мкм).
2. Масса фотона определяется исходя из закона о взаимосвязи массы и энергии (Е=mc2)
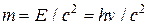 (2)
(2)
3.Импульс фотона. Для любой релятивиской частицы энергия ее 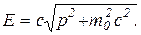 Поскольку у фотона m0=0, то импульс фотона
Поскольку у фотона m0=0, то импульс фотона
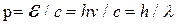 (3)
(3)
т.е. длина волны обратно пропорциональна импульсу.
8.2. Давление света
сdt Пусть на прощадку dS падает и поглощается свет. За время dt





 dS на площадку dS попадут все фотоны находящиеся в объеме dV=cdtdS. Их число N=ndV =n cdtdS, где n - oбъемная плотность
dS на площадку dS попадут все фотоны находящиеся в объеме dV=cdtdS. Их число N=ndV =n cdtdS, где n - oбъемная плотность
фотонов(число фотонов в единице объема). Эти фотоны
передадут площадке импульс dР=pN=(hv/c) n cdtdS и создадут давление
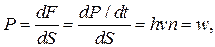 Па (5)
Па (5)
где w- объемная плотность падающей электромагнитной энергии, измеряется в Дж/м3 (Дж/м3=Н×м/м3=Н/м2=Па).
При полном отражении света давление удваивается Р=2w, при отражении с коэффициентом r =(1+ r)w. (6)
8.3.Внешний фотоэффект и его законы. Уравнение Эйнштейна для внешнего фотоэффекта
Испускание электронов веществом под действием света называется внешним фотоэффектом.

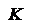 C А.Г. Столетов (1988 г.) экспериментально исследовал фотоэффект.
C А.Г. Столетов (1988 г.) экспериментально исследовал фотоэффект.
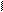




|




 Схема опыта представлена на рис.1. Плоский конденсатор, одной из пластин,которого служила медная сетка С, а в качестве второй
Схема опыта представлена на рис.1. Плоский конденсатор, одной из пластин,которого служила медная сетка С, а в качестве второй 

 цинковая пластина К, был включен через гальванометр G в цепь
цинковая пластина К, был включен через гальванометр G в цепь



 аккумуляторной батареи. Напряжение между пластинами
аккумуляторной батареи. Напряжение между пластинами
Рис.1. измерялось вольтметром. При освещении отрицательно заряженной пластины К светом, в цепи возникал электрический ток, называемый фототоком.
На рис. 2. приведены зависимости фототока I от напряжения U между электродами при различных интенсивностях света (энергетической освещенности E) .
Столетов установил следующие закономерности внешнего фотоэффекта:
 I 1. Максимальная начальная скорость фотоэлектронов
I 1. Максимальная начальная скорость фотоэлектронов

 Iнас1 E2 определяется частотой света и не зависит от его
Iнас1 E2 определяется частотой света и не зависит от его
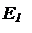 интенсивности.
интенсивности.



 Iнас2 2. Для каждого вещества (катода) cуществует красная
Iнас2 2. Для каждого вещества (катода) cуществует красная

 граница фотоэффекта, т.е. минимальная частота
граница фотоэффекта, т.е. минимальная частота
v0, при которой еще возможен фотоэффект.
-U0 Рис.2 U 3.Фототок насыщения пропорционален
энергетической освещенности Е катода.
Первые два закона не удается объяснить на основе классической теории, согласно которой вырывание электронов из катода является результатом их "раскачивания" электромагнитной волной, которое должно усиливаться при увеличении интенсивности света.
Внешний фотоэффект хорошо объясняется квантовой теорией. Согласно этой теории, электрон получает сразу целиком всю энергию фотона e=hv, которая расходуется на совершение работы выхода электрона из вещества (катода) и на сообщение электрону кинетической энергии:
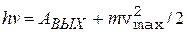 . (7)
. (7)
Это уравнение называется уравнением Эйнштейна для внешнего фотоэффекта.
Из (7) следуют все законы Столетова. В частности, максимальная начальная скорость электронов определяется из соотношения 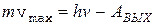 , т.е зависит только от частоты v и материала катода (АВЫХ).
, т.е зависит только от частоты v и материала катода (АВЫХ).
Красная граница v0 соответствует vmax=0
hv0=AВЫХ, v0=AВЫХ/h (8)
При v>v0 (или при l<l0) фотоэффект наблюдается, при v<v0 (или при l>l0) - фотоэффект не наблюдается.
8.4. Эффект Комптона
Заключается в увеличении длины волны рентгеновского излучения при его рассеянии веществом. Изменение длины волны
 Dl=lк(1-cosq)=2lкsin2(q/2), (9) l'
Dl=lк(1-cosq)=2lкsin2(q/2), (9) l'
|
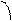



 где lк=h/(mc) - комптоновская длина волны,
где lк=h/(mc) - комптоновская длина волны, 


 m - масса покоя электрона. lк=2.43×10 -12 м= l
m - масса покоя электрона. lк=2.43×10 -12 м= l
 =0.0243
=0.0243 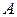 (1 A=10-10 м). Рис. 3
(1 A=10-10 м). Рис. 3
Все особенности эффекта Комптона удалось объяснить, рассматривая рассеяние как процесс упругого столкновения рентгеновских фотонов со свободными электронами, при котором соблюдается закон сохранения энергии и закон сохранения импульса.
Согласно (9) изменение длины волны Dl зависит только от угла рассеяния q и не зависит ни от длины волны l рентгеновского излучения, ни от вида вещества.
8.5. Корпускулярно- волновой дуализм электромагнитного излучения
Итак, изучение теплового излучения, фотоэффекта, эффекта Комптона показало, что электромагнитное излучение (в частности, свет), обладает всеми свойствами частицы (корпускулы). Однако большая группа оптических явлений - интерференция, дифракция, поляризация свидетельствует о волновых свойствах электромагнитного излучения, в частности, света.
Что же представляет собой свет - непрерывные электромагнитные волны, излучаемые источником или поток дискретных фотонов, беспорядочно испускаемых источником? Необходимость пользоваться при объяснении экспериментальных фактов различными и как будто исключающими друг друга представлениями кажется искусственной.
Одним из наиболее значительных достижений современной физики служит постепенное убеждение в ошибочности противопоставления волновых и квантовых свойств света (излучения). Свойства непрерывности, характерные для электромагнитной волны, не исключают свойств дискретности, характерных для фотонов.
Свет (электромагнитное излучение) одновременно обладает свойствами непрерывных электромагнитных волн и свойствами дискретных фотонов. В этом заключается корпускулярно-волновой дуализм (двойственность) электромагнитного излучения.
Ниже будет показано, что корпускулярно-волновыми свойствами обладают и элементарные частицы.
