Лекция 2. Электромагнитные волны
Во второй части курса физики изучались уравнения Максвелла, которые в дифференциальной форме (т.е. справедливые для бесконечно малого объема среды) имели вид:
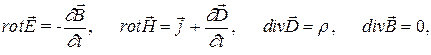 (1)
(1)
где  и
и 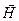 - векторы напряженности электрического и магнитного полей, которые измеряются соответственно в В/м и А/м;
- векторы напряженности электрического и магнитного полей, которые измеряются соответственно в В/м и А/м; 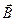 - вектор магнитной индукции (Тл),
- вектор магнитной индукции (Тл), 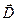 - вектор электрического смещения (Кл/м2),
- вектор электрического смещения (Кл/м2), 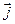 - вектор плотности тока проводимости (А/м2), r - объемная плотность заряда (Кл/м3).
- вектор плотности тока проводимости (А/м2), r - объемная плотность заряда (Кл/м3).
Кроме того, необходимо учитывать, что
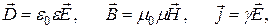 (2)
(2)
где e0=1/(4p×9×109) Ф/м, m0=4p×10-7Гн/м – электрическая и магнитная постоянные; ε, μ – диэлектрическая и магнитная проницаемости среды; g - удельная электропроводность среды ( величина, обратная удельному сопротивлению), а также, что
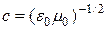 (3)
(3)
- скорость света в вакууме, с = 3×108 м/с.
Скорость распространения электромагнитных волн в среде
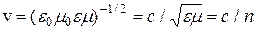 , (4)
, (4)
где 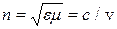 (5)
(5)
- абсолютный показатель преломления среды, он показывает во сколько раз скорость света v в среде меньше скорости света в вакууме с.
Из первого уравнения Максвелла следует, что переменное (изменяющееся во времени) магнитное поле вызывает переменное электрическое поле , а оно [согласно второму уравнению (1) ], изменяясь, вызывает магнитное поле и т.д. Нельзя создать только электрическое поле, не вызвав магнитного поля и наоборот. Т.е. электрическое и магнитное поля взаимосвязаны. Они образуют единое электромагнитное поле, которое распространяется в пространстве (среде) в виде электромагнитных волн.
2.1. Волновые уравнения
Электромагнитные волны удовлетворяют уравнениям аналогичным (1.9)* [* здесь и далее при ссылке на формулы из других лекций сначала дается номер лекции, а затем номер формулы в этой лекции, например (1.9) означает формулу (9) в 1-й лекции.], которые выводятся из уравнений Максвелла с применением векторного равенства
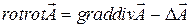
Для линейной однородной изотропной среды при отсутствии токов ( 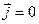 ) и зарядов (r=0) волновые уравнения для векторов
) и зарядов (r=0) волновые уравнения для векторов  и
и 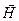 имеют вид
имеют вид
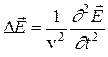 ,
, 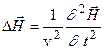 , (6)
, (6)
где 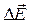 и
и 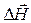 - операторы Лапласа, примененные к векторам
- операторы Лапласа, примененные к векторам  и
и  соответственно, они выражаются через операторы Лапласа от скалярных функций
соответственно, они выражаются через операторы Лапласа от скалярных функций
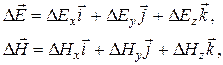 (7)
(7)
где 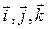 -единичные векторы (орты).
-единичные векторы (орты).
В (1.10) приведено выражение для оператора Лапласа, примененного к скалярной функции.
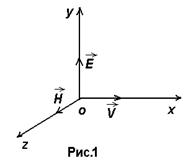 | Будем далее предполагать, что электромагнитная волна распространяется в направлении оси x (см. рис.1.) со скоростью 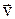 и при этом вектор и при этом вектор  колеблется в одной плоскости, например, в плоскости xoy (эту плоскость называют плоскостью поляризации). Тогда вектор колеблется в одной плоскости, например, в плоскости xoy (эту плоскость называют плоскостью поляризации). Тогда вектор  будет колебаться в перпендикулярной к ней плоскости xoz [это следует из двух первых уравнений (1)], т.е. в такой линейно поляризованной волне векторы будет колебаться в перпендикулярной к ней плоскости xoz [это следует из двух первых уравнений (1)], т.е. в такой линейно поляризованной волне векторы  и и  имеют только имеют только |
по одной составляющей, т.е. 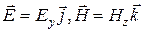 .
.
Следует заметить, что векторы  ,
,  и
и 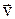 образуют правую тройку взаимноперпендикулярных векторов (т.е. направление вектора
образуют правую тройку взаимноперпендикулярных векторов (т.е. направление вектора 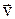 совпадает с направлением поступательного движения правого буравчика, рукоятка которого вращается от
совпадает с направлением поступательного движения правого буравчика, рукоятка которого вращается от  к
к  по наикратчайшему пути).
по наикратчайшему пути).
Для такой линейно поляризованной волны волновые уравнения (6) упростятся и примут вид
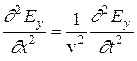 ,
, 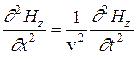 , (8)
, (8)
где индексы y и z при Е и Н подчеркивают лишь то, что векторы  и
и  направлены вдоль взаимно перпендикулярных осей y и z.
направлены вдоль взаимно перпендикулярных осей y и z.
2.2. Уравнение плоской гармонической волны
Уравнениям (8) удовлетворяют, в частности, плоские электромагнитные гармонические волны, описываемые уравнениями
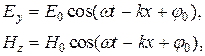 (9)
(9)
где Е0, Н0 – амплитуды напряженностей электрического и магнитного полей, w=2p/Т=2pn - круговая частота (с-1), Т – период колебаний (с) , n=1/Т – частота колебаний (Гц), k=w/v=2p/l - волновое число, v– скорость распространения волны, для нее скорость переноса энергии (групповая скорость) u равна фазовой скорости v этой волны [см.(1.14)]; l=vT – длина волны, для вакуума
l=сT=с/n, (10)
j0 – начальные фазы колебаний в точках с координатой x=0.
В уравнениях гармонической волны (9) j0 - одинаково, т.к. колебания электрического и магнитного векторов в электромагнитной волне происходят в одинаковой фазе [это следует из (1)].
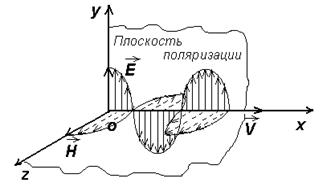 Рис.2 Рис.2 | На рис.2. показаны векторы  и и  поля плоской линейно поляризованной волны в различных точках луча (оси ох) в один и тот же момент времени. Плоскость, проходящая через электрический вектор поля плоской линейно поляризованной волны в различных точках луча (оси ох) в один и тот же момент времени. Плоскость, проходящая через электрический вектор  и луч (или вектор и луч (или вектор 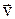 ), называется плоскостью поляризации. Электромагнитную гармоническую волну часто записывают в экспоненци- ), называется плоскостью поляризации. Электромагнитную гармоническую волну часто записывают в экспоненци- |
альной (комплексной) форме аналогично (1.6), где вместо s и А0 будет Е и Е0, Н и Н0 соответственно для электрического и магнитного векторов.
Электромагнитная волна так же, как упругая волна (см. параграф 1.3) характеризуется фронтом волны, волновой поверхностью. В отличие от упругих волн, которые распространяются только в среде (в вакууме упругие волны не могут распространяться, т.к. в нем нет частиц, которые совершали бы колебания), электромагнитные волны распространяются не только в среде, но и в вакууме, т.к. они представляют собой процесс распространения колебаний векторов  и
и  в пространстве.
в пространстве.
Как и в случае упругих волн по форме волновых поверхностей или волновому фронту различают плоские, сферические, цилиндрические и прочие электромагнитные волны.
Обычно в практике используются пучки электромагнитной энергии (света) конечного поперечного сечения. Конечный, но достаточно узкий пучок будем называть лучом. Луч всегда перпендикулярен волновому фронту.
Из уравнений Максвелла (1) следует, что электромагнитные волны являются поперечными волнами, т.к. векторы  и
и  колеблются перпендикулярно к направлению распространения волны (см. рис. 1 и 2).
колеблются перпендикулярно к направлению распространения волны (см. рис. 1 и 2).
Из (1) также следует, что
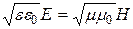 , (11)
, (11)
2.3. Энергия электромагнитной волны
Объемная плотность энергии электромагнитного поля в линейной изотропной среде равна сумме объемных плотностей энергии электрического и магнитного полей [см. Конспект лекций по физике, ч.II, формулы (5.17) и (11.17) соответственно], поэтому
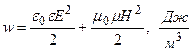 (12)
(12)
С учетом соотношений (11) и (4) из (12) следует, что
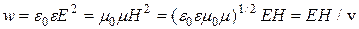 , (13)
, (13)
где v – скорость распространения электромагнитной волны в среде.
В случае плоской линейно поляризованной монохроматической волны (9) объемная плотность энергии волны
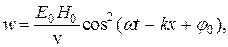 (14)
(14)
т.е значение w в каждой точке поля периодически изменяется от 0 до wмакс=Е0Н0/v за промежуток времени p¤w=T¤2.
Среднее значение объемной плотности энергии волны
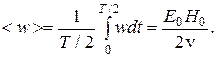 (15)
(15)
Умножив w [см.(13)] на v, получим величину плотности потока энергии
S=wv=EH . (16)
Т.к. векторы  ,
,  и
и 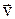 взаимно перпендикулярны и образуют правую тройку векторов, то направление вектора
взаимно перпендикулярны и образуют правую тройку векторов, то направление вектора  ´
´  совпадает с направлением переноса энергии – с направлением вектора
совпадает с направлением переноса энергии – с направлением вектора 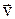 . Поэтому (16) можно записать в векторной форме
. Поэтому (16) можно записать в векторной форме
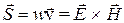 . (17)
. (17)
Вектор плотности потока энергии 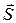 (иногда обозначают
(иногда обозначают 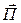 ) направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой волной за единицу времени, через единичную площадку, перпендикулярную направлению распространения волны [см. в параграфе 1.6 Рис.2 и формулы (17), (18)]. S измеряется в Дж/(с×м2)=Вт/м2.
) направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой волной за единицу времени, через единичную площадку, перпендикулярную направлению распространения волны [см. в параграфе 1.6 Рис.2 и формулы (17), (18)]. S измеряется в Дж/(с×м2)=Вт/м2.
Заметим, что в общем случае
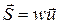 , (18)
, (18)
где u – скорость переноса энергии или групповая скорость.
Для гармонических волн u=v [см.(1.14)] и поэтому можно не различать их.
Интенсивность волны 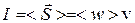 (19)
(19)
С учетом (15 ), (11) следует, что для вакуума (e=m=1)
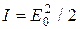 W0, (20)
W0, (20)
где W0=(m0 /e0)-1/2 =120p Ом.
2.4.Излучение электрического диполя
Согласно представлениям классической электродинамики, электромагнитные волны возбуждаются электрическими зарядами, движущимися с ускорением, в частности, электрической цепью (проводом), ток в которой изменяется.
Простейшей излучательной системой является электрический диполь, момент которого (см. параграф 1.5 в конспекте лекций, ч.II) 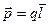 изменяется с течением времени по гармоническому закону p=p0coswt, (21)
изменяется с течением времени по гармоническому закону p=p0coswt, (21)
где р0=ql0 – амплитудное значение момента диполя.
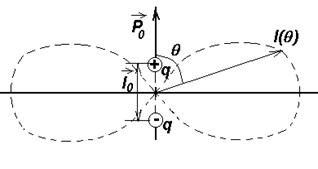 Рис.3 Рис.3 | Средняя мощность, излученная диполем за промежуток времени T=2p/w 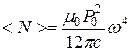 , (22) т.е. пропорциональна квадрату дипольного момента и четвертой степени круговой частоты. При этом диполь излучает не одинаково , (22) т.е. пропорциональна квадрату дипольного момента и четвертой степени круговой частоты. При этом диполь излучает не одинаково |
в различных направлениях. Интенсивность излучения в волновой зоне (т.е. при r>>l0 и r>>l)
I~ sin2q/r2. (23)
На рис. 3 приведена зависимость I(q ) при фиксированном расстоянии от диполя r. Эту зависимость называют диаграммой направленности излучения диполя. Из нее следует, что диполь всего сильнее излучает в направлениях q =p/2 и 3p/2, а вдоль оси диполя (q = 0, p) диполь не излучает совсем.
Рассмотренные выше результаты были использованы в приближенной классической теории излучения атомов, согласно которой это излучение обусловлено колебаниями электронов около их положения равновесия в атомах. В этом случае в формулах (21), (22) p0=еl0 .
Итак, движущийся ускоренно электрон в атоме обладает механической энергией W=mv2/2=mw2l02/2, которую он излучает. В связи с этим колебания электрона являются затухающими. Амплитуда колебаний электрона l0 c течением времени уменьшается по закону l0=l00 exp(-bt), где b - коэффициент затухания, обусловленного излучением энергии.
Промежуток времени t , за который амплитуда колебаний электрона l0 уменьшается в е раз (е = 2,72) называют иногда средним временем жизни излучающего атома. Можно показать, что t ~ l2 и, например, для l=5×10-7 м, соответствующей зеленому свету t = 2,25×10-8 с. (24)
2.5. Шкала электромагнитных волн
В зависимости от длины волны в вакууме l или частоты n=с/l, а также способа излучения и регистрации различают несколько видов электромагнитных волн: радиоволны, оптическое излучение, рентгеновское излучение и гамма-излучение.
Радиоволны образуются при ускоренном движении электронов, т.е. переменными токами. Для радиоволн 104 м > l > 5×10-5 м.
Оптическое излучение возникает при переходе электронов в атомах с верхних энергетических уровней на более низкие, за счет теплового излучения тел (за счет теплового движения зарядов). Для него 1 мм > l > 10 нм(1 нм=10-9 м).
К оптическому излучению относятся инфракрасное (1 мм > l > 770 нм), видимое (770 нм > l > 380 нм) и ультрафиолетовое излучение (380 нм > l > 10 нм).
Рентгеновское излучение возникает при торможении заряженных частиц в веществе, при переходе электронов в атоме с верхних на самые низкие энергетические уровни. Для него 2×10-9 м > l > 6×10-12 м.
Гамма-излучение возникает при ядерных реакциях, для него l< 0,1 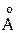 .
.
(1 ангстрем= 10-10 м).
