Расчет удельных сил, действующих в механизме движения

В расчетах динамики шатунно-кривошипного механизма (ШКМ) учитываются силы давления газов и силы инерции движущихся масс и порождаемые ими моменты. Остальные факторы (масса, силы трения) мало влияют на условия нагружения элементов ШКМ двигателя.

Схема сил, действующих в ШКМ, показана на рис. 4.1. Все силы приняты удельными, т. е. отнесены к 1 м² площади поршня.

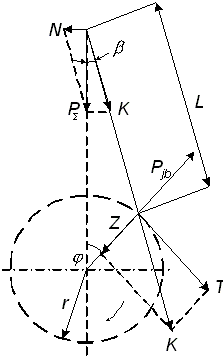
Рис. 4.1. Силы, действующие в
шатунно-кривошипном механизме

Здесь Р_Σ – суммарная удельная сила, приложенная в центре поршневого пальца

P_Σ = P_г + P_j , (4.1)

где Р_г – сила давления газов на поршень (определяется по индикаторной диаграмме); P_j – удельная сила инерции поступательно движущихся масс.

На рис. 4.2 изображена индикаторная диаграмма двс в системе координат PV. Для построения ее в развернутую диаграмму Рφ , где φ – угол в градусах поворота коленчатого вала (упкв), выполняют следующие операции: V_t – полный объем цилиндра; V_s = ad – рабочий объем цилиндра; V_c – объем камеры сжатия; 1–2–3–4–5–1 – индикаторная диаграмма. Пунктирная линия на индикаторной диаграмме – действительный процесс сгорания. Линия аО = Оd – радиус полуокружности;
Δ – поправка Брикса.

Рис. 4.2. Перестроение индикаторной диаграммы
из системы координат PV в развернутую диаграмму Pφ

Линия ad в масштабе равна ходу поршня S. Отрезок аО₁ равен перемещению поршня при повороте коленвала на 90^о от вмт. Отрезок an₂ равен перемещению поршня при повороте коленвала от вмт на угол 180 – φ₂. Отрезок an₁ равен перемещению поршня при повороте коленвала на угол 180 – φ₁. Отрезок an₃ равен перемещению поршня при повороте коленвала на угол 180 – φ₃. Pc₁, Pc₂, Pc₃ – это величины давления на линии сжатия при соответствующем положении поршня в цилиндре. Pp₁, Pp₂, Pp₃ – это величины давления на линии расширения при соответствующем положении поршня в цилиндре. На отрезке ad = V_s находят точку О, из которой радиусом Оа = O₁d описывают полуокружность. Далее определяют поправку Брикса по формуле

Δ = 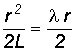, (4.1а)

где r – радиус кривошипа; L – длина шатуна; λ = r/L.

Величину Δ = ОО₁ откладывают в том же масштабе, что и величину отрезка ad. Из точки О₁ через каждые 15^о упкв (для дизелей 10Д100 – через 12^о упкв) откладывают радиусы до пересечения с полуокружностью.

Из точек пересечения радиусов с длиной полуокружности l_1, l_2, l₃ восстанавливаются перпендикуляры. Так как точка n₁ располагается на оси абсцисс, точка f₁ располагается на линии сжатия. Таким образом Pc₁ – это величина давления сжатия в тот момент, когда поршень не дошел расстояние an₁ до верхней мертвой точки (вмт), а коленчатый вал повернулся на угол φ₁ от нижней мертвой точки (нмт).

Точка l₁ находится на закругленной кривой линии расширения учитывающей реальный характер процесса сгорания. Рр₁ – величина давления газов при расширении, когда поршень отошел от вмт на расстояние an₁, а коленчатый вал повернулся от вмт на угол 180 – φ_1.

Аналогично определяют давление сжатия и расширения при других положениях поршня и соответствующем угле поворота коленчатого вала
Рс₂ и Рр₂ при φ₂ и т. д. Таким образом определяется давление газов Р_г в процессах сжатия и расширения. В процессе наполнения величину Р_г принимают равной Р_в (от 0 до 180^о угла поворота коленчатого вала). В процессе выпуска газов Р_г = Р_g1, т. е. равному давлению газов на выпуске в газовую турбину.

Развернутая индикаторная диаграмма, на которой показана сила давления газов Р_г = f (φ) для четырехтактного двс, показана на рис. 4.3.

Рис. 4.3. Зависимость удельных сил Р_г, Р_j , P_å
от угла j для четырехтактного двигателя

К поступательно движущимся массам M_Σn относится масса поршня (в том числе поршневого пальца, поршневых колец и др.) и примерно 0,3 массы шатуна. Остальная часть массы шатуна относится к вращающимся массам.

Силы инерции поступательно движущихся масс, МПа, определяются по уравнению

P_j = – (M_Σn / A) × j × 10^-6 , (4.2)

где А – площадь поршня, м²; j – ускорение поршня в зависимости от угла поворота коленчатого вала φ, м/с².

Поступательно движущаяся масса поршня M_Σп, кг, определиться из выражения:

M_Σn = M_n + 0,3 М_ш, (4.3)

где M_n – масса комплекта поршня; М_ш – масса шатуна.

В прил. 3 даны значения М_п и М_ш;

Ускорение поршня j, м/с², вычисляется по выражению

j = r × w² (cosφ + λ cos2φ), (4.4)

где r – радиус кривошипа, м; w – угловая скорость коленчатого вала, с^-1,

w = π n / 30. (4.5)

При разложении силы P_Σ получаем силу К, МПа, действующую вдоль шатуна и силу N, МПа, направленную нормально к оси, которые определяются по следующим формулам

N = P_Σ × tg β; (4.6)

К = P_Σ (1 / cos β). (4.7)

Далее, силу К переносим в центр шатунной шейки и раскладываем на тангенциальную силу Т, действующую перпендикулярно кривошипу и на силу Z, направленную по кривошипу, которые определяются по формулам

T = P_Σ [sin (φ + β)/ cos β]; (4.8)

Z = P_Σ [cos (φ + β)/ cos β]. (4.9)

Величины тригонометрических функций для различных значений λ = r/L приведены в прил. 6.

Расчет удельных сил удобно производить, сведя все вычисления в табличную форму (прил. 4). На основании вычислений строятся графики зависимостей К = f (φ); N = f (φ); Z = f (φ); Т = f (φ). На рис. 4.3, 4.4, 4.5 приведены соответствующие зависимости сил Р_г, Р_j, Р_Σ, К, N, Т и Z от угла поворота коленчатого вала для четырехтактного двигателя. Для двухтактных двигателей графики строятся для угла поворота в 360°.

Силы Р_г, Р_j, P_Σ, К, Z принимаются положительными, если действуют по направлению к оси коленчатого вала.

Сила N принимается положительной, если направлена против вращения коленчатого вала.

Сила Т положительна, если она направлена в сторону вращения коленчатого вала.

Рис. 4.4. Зависимость удельных сил К и N
от угла j для четырехтактного двигателя

Рис. 4.5. Зависимость удельных сил Т и Z
от угла j для четырехтактного двигателя