Момент инерции. Теорема Штейнера. Кинетическая энергия вращающегося тела.
Момент инерции тела – это мера инертности тела, совершающего вращательные движения.
Моментом инерции J материальной точки относительно оси называется скалярная физическая величина, равная произведению массы m на квадрат расстояния r до этой оси:
J = mr2
Момент инерции тела относительно данной оси – сумма произведений элементарных масс mi на квадраты их расстояний ri2 до рассматриваемой оси.
Момент инерции системы N материальных точек будет равен сумме моментов инерции отдельных точек:
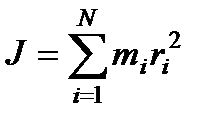
Теорема Штейнера: момент инерции тела J относительно произвольной оси равен моменту его инерции Jc относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния d между осями:
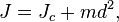
где m — полная масса тела.
Кинетическая энергия вращающегося тела
Определим кинетическую энергию твёрдого тела, вращающегося вокруг неподвижной оси. Разобьем это тело на n материальных точек. Каждая точка движется с линейной скоростью υi=ωri, тогда кинетическая энергия точки
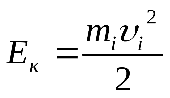 или
или 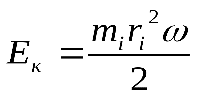
Полная кинетическая энергия вращающегося твердого тела равна сумме кинетических энергий всех его материальных точек:
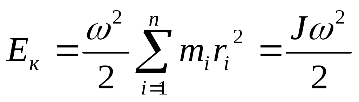 (3.22)
(3.22)
(J - момент инерции тела относительно оси вращения)
Если траектории всех точек лежат в параллельных плоскостях (как у цилиндра, скатывающегося с наклонной плоскости, каждая точка перемещается в своей плоскости), это плоское движение. Плоское движение всегда можно бесчисленным количеством способов разложить на поступательное и вращательное движение. Если шарик падает или скользит вдоль наклонной плоскости, он двигается только поступательно; когда же шарик катится – он ещё и вращается.
Если тело совершает поступательное и вращательное движения одновременно, то его полная кинетическая энергия равна
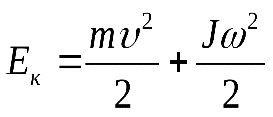
!!27.Основной закон динамики вращательного движения твердого тела.
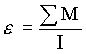
Это основное уравнение динамики вращательного движения тела: угловое ускорение вращающегося тела прямо пропорционально сумме моментов всех действующих на него сил относительно оси вращения тела и обратно пропорционально моменту инерции тела относительно этой оси вращения. Полученное уравнение аналогично по форме записи выражению второго закона Ньютона для поступательного движения тела.
второй закон Ньютона для вращательного движения 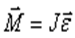 По определению угловое ускорение
По определению угловое ускорение 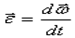 и тогда это уравнение можно переписать следующим образом
и тогда это уравнение можно переписать следующим образом 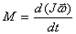 с учетом
с учетом 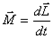 или
или 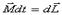
Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела 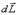 , равно импульсу момента
, равно импульсу момента 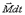 всех внешних сил, действующих на это тело.
всех внешних сил, действующих на это тело.
