Принцип относительности Галилея.

Принцип относительности Галилея: Всякое механическое явление при одних и тех же начальных условиях протекает одинаково в любой инерциальной системе отсчёта.

Т. е. математическая форма второго и третьего законов Ньютона не меняется при переходе от одной инерциальной системы отсчёта к другой.

Доказательство:

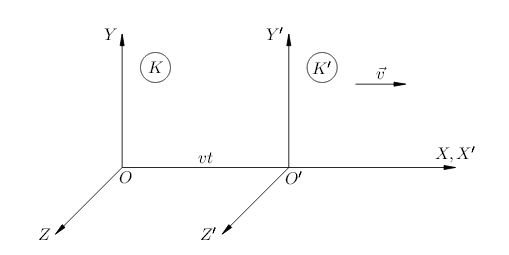
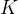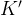Рассмотрим две системы отсчёта: и . Координатные оси этих систем сонаправлены. Систему 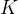будем считать неподвижной. Система 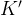движется относительно неё с постоянной скоростью 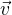вдоль общего направления осе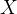й и .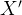

В тот момент, когда начала координат 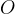и 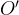совпадали, часы обеих систем были выставлены на ноль и запущены. Стало быть, часы в системах 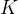и 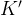идут синхронно, показывая одно и то же время 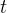. В момент времени 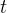расстояние 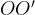равно .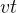

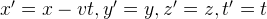
Или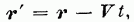

rиr’ – радиус-векторы движущейся точки в системах 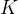и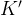

Формулы называются преобразованиями Галилея. Они связывают координаты и время одного и того же события, измеренные в разных инерциальных системах отсчёта: в движущейся системе 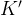и неподвижной системе .

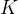Пусть наша частица имеет в системе 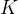скорость 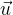, а в системе 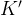— скорость .

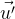Продифференцировав 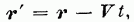по времени и учитывая, что время в двух системах одинаково, мы получим

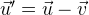
- Закон сложения скоростей в классической механике

Дифференцируем по времени ещё рази производная постоянной величины 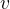обращается в нуль, и мы получаем равенство ускорений:

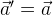
Т. е. ускорение материальной точки не изменяется при переходе от одной инерциальной системы к другой, следовательно, является инвариантом

Следовательно:

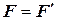(приняли во внимание, что масса в классической механике одинакова во всех системах)

22.Работа и энергия. !!Работа переменной силы. Мощность. Единицы измерения.

Энергия — универсальная мера всех форм движения и взаимодействия. В зависимости от вида движения энергию условно разделяют на: механическую, тепловую, электромагнитную, ядерную и др. В одних явлениях форма движения материи не изменяется (например, горячее тело нагревает холодное), в других — переходит в иную форму (например, в результате трения меха­ническое движение превращается в тепловое). Однако существенно, что во всех случаях энергия, отданная (в той или иной форме) одним телом другому телу, равна энергии, полученной последним телом.

Механическая работа – это физическая величина, численно равная произведению модуля силы, действующей на тело, на модуль перемещения, которое совершает тело под действием этой силы, и на косинус угла между направлением силы и направлением движения тела:

А=F_ss = Fs cos a.

Работа равна нулю, когда тело движется по инерции (F = 0), когда нет перемещения (s = 0) или когда угол между перемещением и силой равен 90° (cos а = 0). Единицей работы в СИ служит джоуль (Дж).

s- путь, пройденный телом

F_s = Fcos a – проекция силы на направление перемещения

Работа-скалярная величина:

При а < она положительна

При а > она отрицательна

При а = (сила перпендикулярна перемещению) равна нулю.

1 джоуль - это такая работа, которая совершается силой 1 Н при перемещении тела на 1 м по линии действия силы.

!!При выполнении этих требований работу, совершаемую при каждом малом перемещении, можно рассчитать по такой же формуле, как и для постоянной силы, т. е.

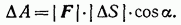
В формулу входят только модули силы и приращения длины пути. Так как |ΔS|= |Δr| то эта формула может быть переписана в следующем виде:

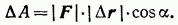
Так проявляется зависимость между работой и векторами перемещений тела. Можно сказать, что работа силы при малом перемещении равна произведению модуля силы на модуль вектора перемещения и на косинус угла между этими векторами. Таким образом, оказалось, что для расчета работы силы нужно произвести действие умножения двух векторов.

Мощность— физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени

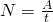
Из формулы следует, что в системе СИ единицей мощности является 1 Дж/с (джоуль в секунду). Эту единицу иначе называют ватт (Вт), 1 Вт= 1 Дж/с. Мощность показывает, какая работа совершается за единицу времени

Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:

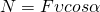
Формула показывает связь между мощностью и скоростью при равномерном движении. Так же формула справедлива и для переменного движения, если под N понимать мгновенную мощность, а под V — мгновенную скорость). Если направление силы совпадает с направлением перемещения, то 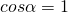и N=Fv. Отсюда:

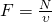
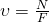
Из этих формул видно, что при постоянной мощности двигателя скорость движения обратно пропорциональна силе тяги и наоборот. На этом основан принцип действия коробки скоростей (коробки перемены передач) различных транспортных средств.

В формуле мы использовали :

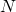— Мощность

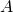— Выполненная работа

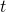— Время, за которое выполнялась работа

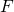— Сила, приложенная к телу

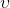— Скорость тела

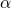— Угол между силой и скоростью