Основные физические свойства жидкости и газа.

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Ухтинский государственный технический университет»

(УГТУ)

Пятибрат В.П.

основы гидравлики

Учебное пособие

Ухта 2017

УДК [532+533.6](075.8)

П99

Пятибрат В. П. Основы гидравлики: Учебное пособие. – Ухта: УГТУ, 2017. – 100 с., ил.

ISBN 5-88179-097-9

Методические указания к выполнению контрольной работы для студентов специальностей ПГС, ВВ, ТГВ безотрывной формы обучения / В. П. Пятибрат. - Ухта: УГТУ, 2017. - ?? с., ил.

Учебное пособие предназначено для студентов дневной и безотрывной формы обучения специальностей: 270102 ²Промышленное и гражданское строительство², 270109 ²Теплогазоснабжение и вентиляция², 270112 “Водоснабжение и водоотведение”.

В учебном пособие приведены основы теории, варианты контрольных заданий, примеры расчетов и справочные материалы.

Содержание указаний соответствует рабочей учебной программе.

Учебное пособие рассмотрено и одобрены кафедрой “Разработка и эксплуатация нефтяных и газовых месторождений и подземная гидромеханика” ?? июня 2010 г. пр. N ?? и рекомендованы к изданию.

Рецензент Сорокин Н. А., к.т.н. доцент кафедры “Безопасности жизнедеятельности и вентиляции”.

Редактор

В методических указаниях учтены замечания рецензента и редактора.

План 2013 г., позиция ??. Подписано в печати ??.??.05 г.

Формат 60x84 1/16. Бумага офсетная. Печать трафаретная.

Объем ?? с. Тираж 50 экз. Заказ №??.

ISBN 5-88179-097-9

© Ухтинский государственный

технический университет, 2013

169300, г. Ухта, ул. Первомайская, 13.

Отдел оперативной полиграфии УГТУ.

169300, г. Ухта, ул. Октябрьская, 13.

содержание

ВВЕДЕНИЕ.. 5

1. Гидростатика. 7

1.1. Основные физические свойства жидкости и газа. 7

1.2. Вязкость жидкости. 10

1.3. Силы, действующие в жидкости. 12

1.4. Абсолютное давление и его свойства. 13

1.5. Дифференциальные уравнения равновесия жидкости. 14

1.6. Поверхность равного давления и ее свойства. 16

1.7. Основное уравнение гидростатики. 16

1.8. Приборы для измерения абсолютного, манометрического давлений и давления вакуума. 17

1.9. Сила давления жидкости на наклонную плоскую стенку. 18

1.10. Точка приложения силы давления жидкости на плоские стенки. 20

1.11. Сила давления жидкости на криволинейные поверхности. 22

1.12. Примеры и задачи. 24

2. Основы кинематики и динамики жидкости. 30

2.1. Основные понятия и определения гидродинамики. 30

2.2. Уравнение неразрывности потока. 33

2.3. Уравнение Бернулли для струйки идеальной жидкости. 36

2.4. Уравнение Бернулли для струйки и потока реальной жидкости. 37

2.5. Интерпритации уравнения Бернулли. 39

2.6. Примеры и задачи. 42

3. Гидравлические сопротивления. 46

3.1. Виды гидравлических сопротивлений. 46

3.2. Ламинарное и турбулентное движение жидкости. 48

3.3. Основное уравнение равномерного движения. 50

3.4. Ламинарный режим движения. 52

3.5. Турбулентный режим движения. 53

3.6. Экспериментальные исследования коэффициента гидравлического сопротивления 55

3.7. Примеры и задачи. 57

4. Гидравлический расчет трубопроводов. 59

4.1. Расчет коротких трубопроводов. 59

1.4.1. Уравнение простого трубопровода. 59

1.4.2. Первый тип расчета. 61

1.4.3. Второй тип расчета. 61

1.4.4. Третий тип расчета. 63

4.2. Расчет газопроводов при малых перепадах давлений. 65

4.3. Примеры и задачи. 66

4.4. Расчет газопроводов при больших перепадах давлений. 66

4.5. Гидравлический удар в трубах. 69

4.6. Примеры и задачи. 75

5. Гидравлический расчет истечения жидкостей. 79

5.1. Истечение жидкости из малого отверстия в тонкой стенке. 79

5.2. Истечение жидкости через внешний илиндрический насадок. 82

5.3. Примеры и задачи. 86

5.4. Примеры и задачи. 86

6. Равномерное движение жидкости в открытых руслах. 87

6.1. Предварительные замечания. 87

6.2. Гидравлические элементы живого сечения потока в канале. 88

6.3. Основные расчетные формулы для открытых русел. 89

6.4. Основные задачи при расчете трапецеидальных каналов на равномерное движение воды. 90

6.5. Примеры и задачи. 91

7. Литература. 92

ВВЕДЕНИЕ

Изучение курса «Гидравлика» в заочных вузах включает в себя работу с книгой, решение задач, выполнение контрольной работы.

В контрольную работу входят три задания. Каждое задание содержит две задачи и четыре вопроса.

Первое контрольное задание посвящено физическим свойствам жидкостей и гидростатике. Второе задание включает основные уравнения гидравлики и гидравлические сопротивления. Третье задание посвящено расчету трубопроводов для жидкостей, газов и истечению жидкостей из отверстий и насадков.

Задания, оформленные соответствующим образом, студент высылает в университет для проверки. Только после выполнения контрольной работы студент допускается к зачету по гидравлике.

В связи с инженерным характером курса большую роль играет решение расчетных примеров и задач. Приступая к самостоятельному решению задачи, студент должен предварительно обдумать схему решения, найти нужные формулы. Выполненная в масштабе расчетная схема оказывает, как правило, большую помощь. При решении задач чрезвычайно важно следить за соблюдением правильной размерности всех входящих величин. Недостаточное внимание к размерности является наиболее частой причиной ошибок. При выполнении работы следует пользоваться Международной системой единиц измерения (СИ).

ВВЕДЕНИЕ

Изучение курса «Гидравлика и аэродинамика» в заочных вузах включает в себя работу с книгой, решение задач, выполнение лабораторных работ и четырех контрольных заданий.

Первое контрольное задание выполняется на третьем курсе; оно посвящено физическим свойствам жидкостей и гидростатике. Второе, третье и четвертое задания выполняются на четвертом курсе. Второе задание включает основные уравнения гидравлики и гидравлические сопротивления. Третье задание посвящено расчету трубопроводов для жидкостей и газов и сопротивлению тел в потоке. Четвертое - охватывает материалы, относящиеся к истечению жидкостей и гидравлическому моделированию.

Каждое контрольное задание включает контрольные вопросы, на которые должны быть даны письменные ответы, а также контрольные задачи, решение которых следует представить. Контрольные задания рекомендуется выполнять по мере изучения соответствующих разделов курса и ознакомления с решением типовых задач.

Задания, оформленные соответствующим образом, студент высылает в институт для проверки. Только после получения зачета по всем четырем, заданиям, а также выполнения и защиты лабораторных работ студент допускается к экзамену по гидравлике и аэродинамике. При сдаче экзамена он должен предъявить экзаменатору четыре зачтенных контрольных задания и дополнительно их защитить.

В связи с инженерным характером курса большую роль играет решение расчетных примеров и задач. Приступая к самостоятельному решению задачи, студент должен предварительно обдумать схему решения, найти нужные формулы. Выполненная в масштабе расчетная схема оказывает, как правило, большую помощь. При решении задач чрезвычайно важно следить за соблюдением правильной размерности всех входящих величин. Недостаточное внимание к размерности является наиболее частой причиной ошибок. При выполнении работы следует пользоваться Международной системой единиц измерения (СИ).

Гидростатика

Вязкость жидкости.

Вязкостью называют свойство реальных жидкостей оказывать сопротивление движению слоёв жидкости друг относительно друга. Это свойство не может быть обнаружено при покое жидкости, так как оно проявляется лишь при ее движении.

Чтобы выяснить физическую сущность понятия вязкости, рассмотрим следующую схему. Пусть имеются слой жидкости толщиной y (рисунокрисунок 1.1). Нижний слой жидкости соприкасается с твердым телом и неподвижен. На верхнем слое находится твердая, невесомая пластина площадью w, к которой приложена сила T и поэтому она движется со скоростью u. При этом, как показывает опыт, промежуточные слои будут скользить один по другому со скоростью, пропорциональной их расстоянию до нижней пластинки.

Рисунок 1.1 – К определению вязкости жидкости - Пояснение свойства вязкости жидкости

Еще Ньютон высказал предположение, что силы сопротивления, возникающие при таком скольжении слоев, пропорциональны площади соприкосновения слоев и скорости скольжения. Тогда сила, которую нужно приложить к пластинке, чтобы она двигалась со скоростью u, равна:

(1.15)

где μ - – коэффициент динамическая вязкость жидкости, зависит от рода жидкости.

Таким образом, вязкостью жидкости называетсявязкость есть физическое свойство жидкости, оказывать сопротивление движению слоёв жидкости друг относительно другахарактеризующее ее сопротивляемость скольжению или сдвигу.

Единицей измерения динамической вязкости является паскаль на секунду (Па·с) или мПа·с = 10^-3 Па·с. В справочниках встречаются старые единицы измерения динамической вязкости 1 пуаз = 1 г/см·с = 0,1 Па·с.

Динамическая вязкость воды зависит от температуры и может быть рассчитана по формуле:

(1.16)

где μ - – кинематическая вязкость, Па·с;

t - – температура, °С.

Коэффициентом кинематической вязкости жидкости n называется отношение коэффициента динамической вязкости жидкости к плотности:

(1.17)

Единицей кинематической вязкости является квадратный метр на секунду (м²/с).

Вязкость различных сортов жидкости одного названия, например, нефти, в зависимости от химического состава и молекулярного строения может иметь различные значения.

Температурная зависимость вязкости нефти хорошо описывается формулой:

(1.18)

где n₁ - кинематическая вязкость нефти при температуре t₁,

u - коэффициент, который определяетсяустанавливаемый по экспериментальным данным.

Для определения коэффициента u необходимо знать вязкость нефти ν₁ и ν₂ при температуре t₁ и t₂:

(1.19)

Вязкость жидкостей, как показывают опыты, зависят также от давления. При возрастании давления она обычно увеличивается.

Коэффициенты динамической и кинематической вязкости газов с повышением температуры увеличиваются.

Касательным напряжением t называется отношение силы действующей к поверхности касательно к величине площади этой поверхности w:

.

(1.20)

Касательные напряжения имеют размерность давления (Па). Тогда закон Ньютона внутреннего трения в жидкости запишется:

.

(1.21)

Для линейной зависимости скорости координатой y касательные напряжения везде в потоке одинаковые. Если зависимость нелинейная, то формулу (2.15) необходимо записать для двух бесконечно близких пластинок:

.

(1.22)

Жидкость называется идеальной, если обладает следующими свойствами:

· абсолютно подвижна, μ = 0;

· абсолютно несжимаема, β_p = 0;

· не изменяет свой объём при изменении температуры β_t = 0,

Идеальной жидкости в природе нет, но есть типы движения жидкости, когда её можно считать идеальной.

Примеры и задачи

Пример 1.1.

Плотность и объем первой жидкости равны 1000 кг/м³ и 6 см³. Плотность и объем второй жидкости 800 кг/м³ и 4 см³. Определить плотность смеси этих жидкостей.

Решение:

По определению плотности масса первой и второй жидкости равны:

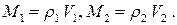
Плотность смеси находим по определению:

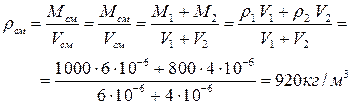
Ответ: плотность смеси равна 920 кг/м³

Пример 1.2.

Проводятся гидравлические испытания водопровода длиной 5 км и диаметром 2 м. Необходимо повысить давление в нём до 4 МПа. Какой объём воды необходимо дополнительно закачать в водопровод? Коэффициенты объёмного сжатия принять равными 5 10^-10 1/Па.

Решение:

Из определения коэффициента объёмного сжатия жидкости следует, что изменение объёма воды равно 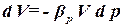. Объём жидкости в трубе – это объём цилиндра диаметром D и длиной ℓ. Поэтому

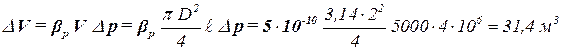
Ответ: необходимо закачать 31,4 м³ воды.

Пример 1.3.

Определить плотность воды при температуре 44 Сº, если при температуре 4 Сº плотность воды 1000 кг/м³. Коэффициент температурного расширения воды принять равными 4,8 10^-4 1/Сº.

Решение:

Обозначим величины при температуре 4 Сº индексом 1, а при температуре плотность 44 Сº индексом 2. Тогда плотность жидкости при температуре 44 Сº равна:

.

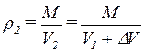Изменение объёма воды при изменении температуры найдём из определения коэффициента температурного расширения: .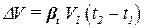

Тогда плотность воды будет равна:

.

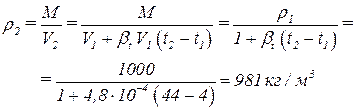Ответ: плотность воды при температуре 44 Сº равна 981 кг/м³.

Пример 1.4.

В баке компрессора воздух находится при давлении 0,2 МПа и температуре 20 Сº. В баке образовалось отверстие, через которое происходит истечение воздуха в атмосферу (p_ат = 0,1 МПа). Определить температуру вытекающего воздуха.

Указание: процесс истечения считать адиабатическим (k = 1,5).

Решение:

Обозначим величины в баке компрессора индексом 1, а истекающего воздуха индексом 2. Запишем уравнения состояния и уравнение процесса:

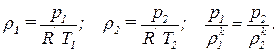
Из этих уравнений исключаем плотности:

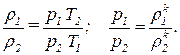
Откуда:

.

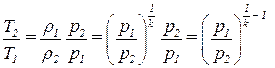Тогда температура воздуха при истечении равна

.

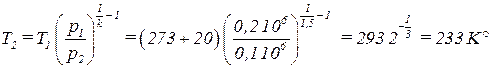Или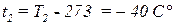

Ответ: температура истекающего воздуха равна - 40 .

Пример 1.5.

Вертикальная стенка длиной ℓ=3 м (в направлении, перпендикулярном плоскости чертежа), шириной b = 0,7 м и высотой Н₀ = 2,5 м разделяет бассейн с водой на две части. В левой части поддерживается уровень воды H₁ =2 м, в правой - H₂ = 0,8 м.

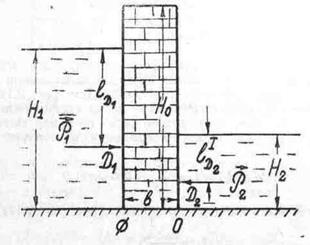Рисунок 1.10 - - Схема к примеру 1.5

Найти величину опрокидывающего момента, действующего на стенку, а также определить, будет ли стенка устойчива против опрокидывания, если плотность материала стенки ρ = 2500 кг/м³.

Решение:

Найдем силу давления воды на стенку слева. Так как на поверхности давление атмосферное, то пьезометрическая плоскость совпадает с поверхностью жидкости,

.

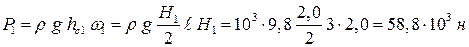Стенка вертикальная, поэтому расстояние от линии уреза до центра тяжести равно глубине погружения центра тяжести ℓ_c1 = h_c1 = H₁/2. Момент инерции поверхности относительно линии, параллельной линии уреза и проходящей через центр тяжести равен .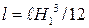

Тогда координата центра давления:

.

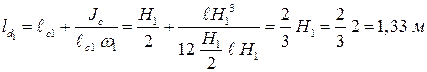Точно также справа

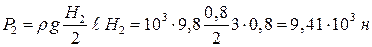kH,

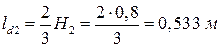M.

Опрокидывающий момент, то есть момент сил давления жидкости относительно точки О (см. рисунок 2.9), равен:

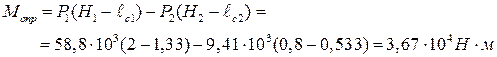
Устойчивость против опрокидывания сообщает стенке момент ее силы тяжести относительно точки О, равный:

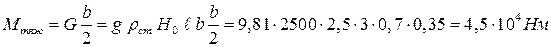
Так как M_тяж > M_опр, то стенка устойчива.

Пример 1.6.

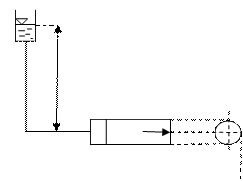Рисунок 1.11 - Схема к примеру 2.6

Определить давление жидкости на плоские боковые стенки цилиндрического резервуара, если его диаметр D=3 м (рисунок 2.10).

Решение:

Для этого сначала найдем силу давления Р (для избыточного давления).

Давление в центре тяжести площади стенки p = r g h = 9,81×1000×15 = 1,47×10⁴, откуда:

P = p_c w = p_c p×d²/4 = 1,47×10⁴×p×d²/4 = 1,03×10⁵ Н.

Пример 1.7.

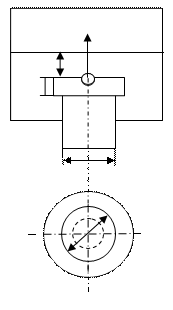Рисунок 1.12 - - Схема к задаче 1.7

Определить усилие U, необходимое для того, чтобы поднять клапан (рисунок 2.11), если диаметр головки D = 0,5 м, диаметр цилиндрического ствола d = 0,3 м, высота головки а = 0,25 м и глубина погружения клапана h=1,25 м. Вес клапана G=29,4 H.

Решение. Необходимое усилие U находим из условия предельного равновесия

,

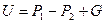где 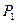и 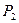- силы давления жидкости на верхнюю и нижнюю (кольцевую)

поверхности головки клапана. Вычисляем последовательно:

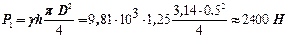
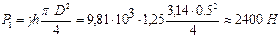
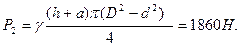
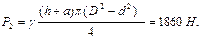
Искомое усилие 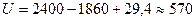Н.

Пример 1.8.

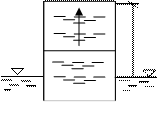Рисунок 1.13 - К задаче 1.8

Определить силу R давления жидкости на горизонтальное дно резервуара (внутреннее давление снизу вверх) в соответствии с рисуно 2.12, если 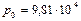Па; d=2 м.

Решение:

Искомая сила R = p ω, где p - гидростатическое давление в центре тяжести площади ω (в точке М).

По формуле:

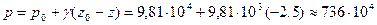
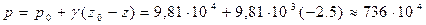Па, откуда

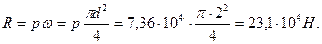
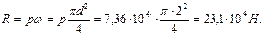
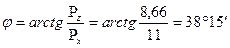
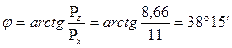
Задача 1.1

Стальная труба с внутренним диаметром D = 600 мм. работает под давлением р = 3 МПа. Найти : а) необходимую толщину стенок трубы , если допустимое напряжение для стали 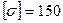МПа ; б) максимально допустимое давление при толщине стенки трубы 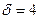мм.

Ответ: а) 6 мм.; б) 2 МПа (20,4 кгс/см²).

Задача 1.2

Найти силу давления воды на дно сосуда диаметром D = 1 м , если глубина H=0,7м, вес поршня G = 300 Н, d=0,5 м.

Ответ: 6,59 кН.

Задача 1.3

Наклонный прямоугольный щит плотины шарнирно закреплен на оси О. При каком уровне воды Н щит опрокинется, если угол наклона щита a=60°, а расстояние от его нижней кромки до оси шарнира d=1,3 м. Вес щита не учитывать.

Ответ: Н=3,38м.

Задача 1.4

Определить силу давления жидкости на торцевую плоскую стенку горизонтальной цилиндрической цистерны диаметром d=2,4 м, заполненной бензином плотностью r=760кг/м³, если уровень бензина в горловине находится на расстоянии H=2,7 м от дна. Цистерна герметически закрыта и избыточное давление на поверхности жидкости составляет 40 кПа. Найти также положение центра тяжести стенки..

Ответ: P=231 кН, Dl= 0,052 м.

Задача 1.5

Резервуар заполнен нефтью плотностью ρ=850 кг/м³ До высоты H=4 м . Избыточное давление на поверхности pн= 14,7 кПа. Определить реакции шарнира A и стяжного болта В крышки люка, если диаметр патрубка d=1м и его центр расположен на расстояниях H=1,5 м от дна резервуара, а=0,7 м и b=0,8 м. Вес крышки не учитывать.

Ответ: ra = 14.7 кН, rB = 13,4 кН.

Примеры и задачи

Пример 2.1.

Идеальный газ движется в сужающейся трубе. Во сколько раз скорость газа в узком сечении больше, чем в широком, если: D₁ = 1,5 D₂, P₁ = 1,2 P₂. Движение газа изотермическое.

Решение:

При установившемся движении сжимаемой жидкости сохраняется массовый расход:

.

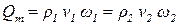Найдем отношение скорости в узком (втором) поперечном сечении к скорости в широком поперечном сечении:

.

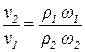Так, как движение изотермическое, то плотности газа зависят от давления линейно:

,

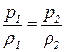Откуда

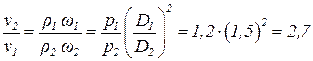
Ответ: скорость газа во втором сечении в 1,8 раза больше, чем в первом.

Пример 2.2.

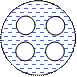В водо - -водяном теплообменнике жидкость движется в межтрубном пространстве. ВнутреннийВнитренний диаметр корпуса D = 0,2 м, а внешний диаметр каждой из четырёх (n = 4) латунных трубок d = 0,05 м. Определить эквивалентный диаметр для потока и скорость движения жидкости в поперечном сечении (затемненная область), если за 100 секунд прокачивается 1,57 м³ воды.

Решение:

Площадь поперечного сечения потока равна разности площадейплошадей корпуса и всех латунных трубок:

.

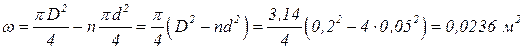Смоченный периметр равен сумме периметра корпуса и периметра всех латунных трубок

.

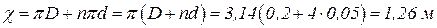
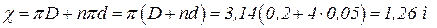Тогда эквивалентный диаметр равен четырём гидравлическим радиусам:

.

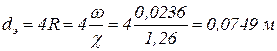
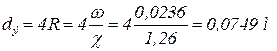СкоростьСкороть воды в межтрубном пространстве равна:

.

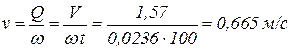
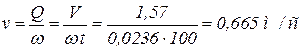Ответ: v = 0,665 м/c; d_э = 0,0749 м.

Пример 2.3.

По трубе диаметром d₁ = 0,2 м движется вода. В трех точках производится отбор воды с расходами Q₁ = 0,01 м³/с, Q₂ = 0,03 м³/с, Q₃ = 0,02 м³/с. Определить скорости на участках трубопровода.

Решение:

Расход на участке от входа в трубопровод до первой точки отбора равен сумме расходов которые отбираются после этого участка:

Q_вх-1 = Q₁ + Q₂ + Q₃ = 0,01 + 0,03 +0,02 = 0,06 м³/с.

Тогда скорость на этом участке равна:

.

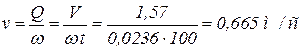
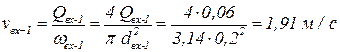На участке между первой и второй точками отбора расход равен сумме расходов которые отбираются после этого участка:

Q_1-2 = Q₂ + Q₃ = 0,03 +0,02 = 0,05 м³/с.

Тогда скорость на этом участке равна:

.

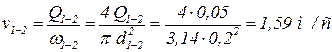На участке между второй и третьей точками отбора расход равен:

Q_2-3 = Q₃ = 0,02 = 0,02 м³/с.

Тогда скорость на этом участке равна:

.

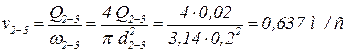Ответ: v_вх-1 = 1,91 м/c; v_1-2 = 1,59 м/c; v_2-3 = 0,657 м/c.

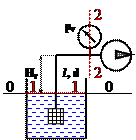Пример 2.4.

Насос за 10 минут перекачивает 6 м³ воды, по трубе диаметром 100 мм. Высота подъёма жидкости H_г = 4 метра. Потери напора рассчитать по формуле h_1-2 = 3 v²/2g, где v – скорость в тубе.

Рассчитать показание вакуумметра.

Решение:

Выберем два поперечных сечения там, где известны давления или где одно из давлений необходимо найти – одно по свободной поверхности жидкости, а второе где стоит вакуумметр.вакууметр. Нумеруем поперечные сечения по направлению движения жидкости в начале потока 1 – 1 в конце 2 – 2 (см. рисунок).

Выбираем плоскость сравнения 0 – 0 проходящую через центр тяжести нижнего поперечного сечения.

Находим значения z и абсолютные давления p в поперечных сечениях:

z₁ = 0; p₁ = p_aт; z₂ = Н_г; p₂ = p_aт – p_v.

Расписывают скорости в поперечных сечениях. Площадь поперечного сечения бака большая, поэтому скорость в первом поперечном сечении можно считать равным нулю, а площадь второго поперечного сечения равна площади поперечноготоперечного сечения трубы, поэтомутоэтому скорость во втором сечении равно скорости в трубе:

v₁ » 0; v₂ = v.

Полученные значения z, p, v подставляют в уравнение Бернулли:

.

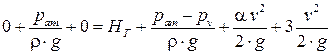Упрощая полученное уравнение, найдем показание вакуумметра:

.

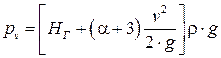Найдём расход жидкости в трубе:

.

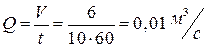Находим скорость в трубе:

.

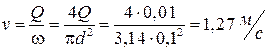Находим давление:

.

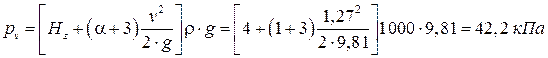Ответ: p_v = 42,2 кПа.

Задача 2.1

По тройнику движется жидкость. Определить скорости движения жидкости в сечениях, если Q1 = 0,0314 м3/с, Q2 = 0,0157 м3/с, а диаметры сечений равны d2 = 0,2 м, d1 = d3 = 0,1 м

Задача 2.2

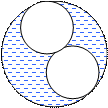Определить эквивалентный диаметр для потока и скорость движения жидкости в поперечном сечении (затемненная область), если за 100 секунд прокачивается 3,14 м3 воды, а диаметры равны D = 0,2 м, d = 0,1 м.

Задача 2.3

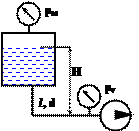Вода из бака перекачивается насосом с расходом 2 л/с по трубопроводу диаметром 30 мм. Высота уровня воды в баке H = 10 м. Давление вакуума на входе в насос pv = 0,03 МПа. Потери напора h1-2 = 7 V2/2g. Рассчитать давление в баке pм.

Задача 2.4

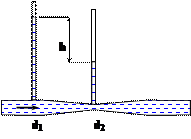В водомере Вентури разность уровней пьезометров равна h = 0,5 м. Определить расход, если диаметры равны d1 = 0,3 м. d2 = 0,2 м. Потери напора считать равными h1-2 =0,06 V22/2g.

Турбулентный режим движения

Турбулентный режим движения существует в трубах, если число Рейнольдса больше критического числа Рейнольдса Re > Re_кр = 2000¸2320. Турбулентный режим движения по своей природе нестационарный режим, поэтому и давления и скорости в любой точке меняются с течением времени. На рисунке 3рисунок.5 приведено изменение составляющей местной скорости вдоль оси x с течением времени u_x(t). Среднее значение этой скорости за достаточно большой промежуток времени называется осреднённой скоростью

(3.23)

Разность местной скорости и осреднённой скорости называется пульсацией скорости u¢_x(t)

(3.24)

Пульсации скорости происходят как вдоль оси трубы, так и по радиусу трубы. Поэтому частицы жидкости, находящиеся у стенки трубы и имеющие маленькую скорость вдоль оси трубы могут оказаться на оси трубы, где большие скорости и будут тормозить эти слои. А частицы жидкости, находящиеся на оси трубы и имеющие большую скорость вдоль оси трубы могут оказаться у стенки трубы, где маленькие скорости и будут ускорять эти слои.

Рисунок 3.5 - Пульсации– пульсации местной скорости в турбулентном потоке.

Поэтому за счет пульсаций скоростей эпюра скорости при турбулентном режиме у стенки быстро возрастает, чем при ламинарном режиме, а на оси трубы эпюра более пологая.

РисунокРисунок 3.6 - Эпюры– эпюры скоростей при ламинарном и турбулентном режиме

Рисунок 3.7 - Структура– структура потока при турбулентном режиме

Рисунок 3.8 - Гидравлически гладкие a – гидравлически гладкая труба,и шероховатые трубы b – гидравлически шероховатая труба

Примеры и задачи

Пример 3.1.

Дано:

Определить пределы изменения гидравлического радиуса К для канализационных самотечных трубопроводов, если диаметр их D изменяется от 150 до 3500 мм. Расчетное (наибольшее) наполнение: а=h/D=0,6 для труб D=150 мм; а=h/D = 0,8 для труб D=3500 мм.

Решение:

Гидравлический радиус определяем по формуле:

R = w/c-X

R=8,22/7,7=1’07м. Таким образом, гидравлический радиус изменяется от 0,04 до 1,07 м.

Пример 3.2.

Определить напор, необходимый для пропуска расхода воды Q=0,=0.01 м3/с через трубопровод диаметром D=0,3 м и длиной 1=1200 м. Трубы стальные новые. Температура 20 градусов С.

Решение:

По таблице находим эквивалентную шероховатость новых стальных труб k_э = 0,22 мм. Для найденной шероховатости и заданного диаметра определяем значение удельного сопротивления трубопровода при работе его в квадратичной области: А_кв=0,504 с²/м⁶

Требуемый напор (в первом приближении) при условии работы трубопровода в квадратичной области

h_кв=А_кв l Q²=0.5*1200*0.07²=3 м.

Задача 3.1

Определить расход воды р в трубе диаметром D = 250 мм, имеющей плавное сужение до диаметра d = 125 мм, если показания пьезометров до сужения: h₁ = 50см; в сужении h₂ = 30 см. Температура воды 20 градусов С.

Задача 3.2

Определить, на какую высоту поднимается вода в трубке, один конец которой присоединен к суженному сечению трубопровода, а другой конец опущен в воду. Расход воды в трубе Q = 0,025 м3/с, манометрическое давление р_м = 49*10³ Па, диаметры D = 100мм и d = 50мм.

Задача 3.3

Выход воды из горизонтальной песколовки выполнен в виде сужения с плавно закругленными стенками. Ширина песколовки В=3м. Расход сточной воды Q = 0,9 м³/с при скорости движения воды V=0,3 м/с. Определить глубину воды в отводящем канале h, если ширина его B = 0,8м.

Задача 3.4

Стальной новый водовод диаметром D = 0,25 м, с абсолютной эквивалентной шероховатостью k₁ = 0,0001м имеет пропускную способность Q ⁼ 0,052м³/с. Вода в источнике слабоминерализованная, некорозионная. Исследования, проведенные через два года после начала эксплуатации, показали, что абсолютная шероховатость трубопровода возросла до k₂ = 0,2мм. Требуется определить, какая будет пропускная способность водовода Q₁ через 15 лет эксплуатации.

Задача 3.5

Потеря давления в стальной водопроводной трубе диаметром D = 0,45 м и длиной 1=3000м, бывшей в эксплуатации в течение 12 лет, составляет р₁ = 10⁵Па при расходе воды Q = 0,2 м³/с. Температура воды 20 градусов С. Требуется определить потери давления р₂ в этой же трубе через 20 лет эксплуатации при расходе воды Q₂ = 0,3 м /с.

Задача 3.6

Определить величину повышения давления в стальной водопроводной трубе, если скорость воды в трубе до удара была V = 1 м/с, диаметр трубы D = 0,5 м, и толщина стенок d = 0,0005.

Первый тип расчета

Пусть по известным данным необходимо рассчитать давление вакуума p_v. В этом случае из уравнения простого трубопровода выразим определяемую величину:

(4.5)

Дальнейший порядок расчета следующий:

Рассчитываем объёмный расход Q = V/t;

Рассчитываем скорость в трубе v = Q/w = 4 Q/(p d²);

Рассчитываем число Рейнольдса Re = v d r/m = v d/n и определяем режим движения жидкости в трубопроводе. Если число Рейнольдса меньше критического Re_кр = 2000¸2320, то режим движения ламинарный, если больше то турбулентный.

Рассчитываем коэффициент гидравлического сопротивления трения

(4.6)

Подставляя полученные значения в уравнение (5.5), найдем неизвестную величину.

Второй тип расчета

Пусть по известным данным необходимо рассчитать скорость или расход в трубопроводе. В этом случае уравнения простого трубопровода будет транцентдентным, то есть его нельзя разрешит относительно скорости так, как скорость входит в это уравнение в явном виде, но и в неявном виде при определении коэффициента гидравлического сопротивления трения l. В этом случае возможны два метода расчета: метод подбора и метод итераций.

Метод подбора.

В уравнения простого трубопровода все известные слагаемые перенесём в левую часть, а неизвестные в правую:

(4.7)

Рассчитываем численное значение левой части.

Дальнейший порядок расчета следующий:

Задаемся произвольным значением скорости в трубопроводе v₀ (скорость в трубопроводе обычно меньше 5 м/с);

Рассчитываем число Рейнольдса и определяем режим движения жидкости в трубопроводе;

Рассчитываем коэффициент гидравлического сопротивления трения l;

Рассчитываем правую часть уравнения;

Сравниваем рассчитанную правую часть уравнения и левую. Если правая часть уравнения меньше левой H_прав < H_лев то задаёмся большим значением новой скорости v₁ > v₀, если же правая часть уравнения больше левой H_прав > H_лев то задаёмся меньшим значением новой скорости v₁ < v₀.

Результаты расчетов удобно поместить в таблицу:

Таблица 4.1 – Подбор скоростей
Скорость, м/с	Re	Режим	l	Hправ
V0	Re0		l0	Hправ0
V1	Re1		l1	Hправ1
V2	Re2		l2	Hправ2

По полученным значениям строим график зависимости правой части уравнения от скорости. Для построения графика необходимо, как минимум три точки. По известной левой части по графику находим необходимую скорость и рассчитываем расход.

Метод итераций

Уравнения простого трубопровода разрешаем относительно скорости:

(4.8)

Индекс i – номер итерации.

Дальнейший порядок расчета следующий:

Задаемся начальным произвольным значением скорости в трубопроводе v₀ с индексом i = 0;

1. Рассчитываем число Рейнольдса и определяем режим движения жидкости в трубопроводе;

2. Рассчитываем коэффициент гидравлического сопротивления трения l₀;

3. По уравнению (5.8) рассчитываем новое значение скорости с индексом i = 1.

Далее пункты 1-3 повторяются с новой начальной скоростью. Итерации проводятся до тех пор, пока первые три значащие цифры скорости не совпадут. Для турбулентного режима движения обычно необходимо провести две - три итерации, для ламинарного режима движения итераций необходимо больше.

Третий тип расчета

Пусть по известным данным необходимо рассчитать диаметр трубопровода. В этом случае уравнения простого трубопровода будет транцентдентным, то есть его нельзя разрешит относительн