Основные свойства жидкости и газа. Гидростатика

I. Курс лекций

Основные свойства жидкости и газа. Гидростатика

Основные свойства жидкости

Система материальных точек, непрерывно заполняющая некоторую часть пространства, называется сплошной средой. Сплошная среда представляет собой модель реально существующих материалов, т.е. яв­ляется определенной идеализацией, полезной для решения многих прак­тических задач. Моделью сплошной среды пользуются для описания жид­ких тел (воды, нефти, нефтепродуктов и т.д.), твердых деформируемых тел (металлов, горных пород), а также газообразных веществ (воздуха, природного газа). Жидкость в гидромеханике рассматривается как сплошная среда, что очень удобно при использовании математического аппарата непрерывных функций.

Плотность характеризует массу сплошной среды (в том числе и жидкости), содержащуюся в единице объема.

Средняя плотность среды в достаточно малом объеме DV, содержа­щем точку М(х, у, z), определяется по формуле

r_ср = Dm/DV, (1.1)

где D m — масса сплошной среды, заключенная в объеме DV.

В точке М плотность равна

r (х, у, z, t) = 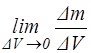. (1.1¢)

Если r не зависит от координат х, у, z, т.е. плотность одна и та же во всех точках среды, то последняя называется однородной.

Наряду с плотностью среды вводится ее удельный вес

g = rg, (1.2)

где g — ускорение свободного падения.

Размерности и единицы измерения для величин r и g приведены ниже.

Величина ………………………. Плотность Удельный вес

Размерность …………………. M/L³ M/(L²T²)

Единица измерения в СИ …….. кг/м³ кг/(м²× с²) или Н/м²

Силы, действующие на частицы сплошной среды, делятся на два вида: массовые и поверхностные.

Силы, распределенные по объему V, называются массовыми силами. Примером таких сил может служить сила тяжести, сила инер­ции, электромагнитные силы.

Массовые силы характеризуются плотностью массовых сил (напряжением массовых сил). Если Dm — масса элементарного объема DV, содержащего точку М(х, у, z), а D 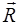— сила, действующая со стороны внешних тел на частицы, входящие в объем DV, то плотность массовых сил 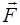точке М(х, у, z) определяется из выражения

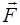(x,y,z,) = 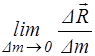. (1.3.)

Плотность массовых сил 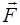— векторная величина и имеет размер­ность ускорения

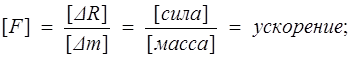
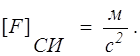
Поверхностные силы представляют собой силы, распределенные по поверхности, ограничивающей рассматриваемый объем. На внешней поверхности тела поверхностные силы отражают взаимодействие тела с окружающей средой. К поверхностным силам относят силы давления, силы реакции тела на поток, силы внутреннего трения в среде.

Поверхностные силы в сплошной среде характеризуются вектором напряжений

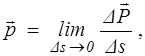(1.4)

где D 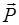— главный вектор сил, приложенных с одной стороны к некото­рой малой площадке Ds.

Напряжение — размерная величина. Размерность напряжения опреде­ляется на основе формулы (1.4) :

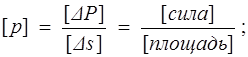
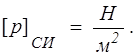
В каждой точке М (х, у, z) сплошной среды можно построить бесконечное число векторов напряжений, определяемых ориентацией выбранной площадки. Каждый из этих векторов может иметь нормаль­ную по отношению к площадке и касательную составляющие.

В покоящейся жидкости отсутствуют касательные напряжения, а нормальные напряжения являются сжимающими. Растяжения в среде, называемой жидкостью, невозможны, а бесконечно малые сдвигающие усилия сразу же вызывают начало течения. Поэтому жидкость принимает форму того сосуда, в который она налита.

Основной характерный параметр для жидкости — давление р. В по­коящейся жидкости модули нормальных напряжений на всех площад­ках, проходящих через данную точку, равны между собой и называются давлением в данной точке.

Давление — это скалярная величина, имеющая размерность напряжения

.

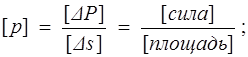
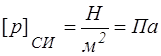Различают давление абсолютное, избыточное и вакуум. Давление р, определенное выше, называют абсолютным. Если за начало отсчета принимается атмосферное давление р_а , то избыток абсолютного давле­ния р над атмосферным называется избыточным давлением p_и= р — р_а. При этом может быть два случая:

1) абсолютное давление р больше р_а, тогда Р_и= р — р_а > 0 и изме­ряется манометрами, поэтому оно называется еще манометричес­ким;

2) абсолютное давление р меньше р_а, тогда р_и =р — р_а < 0, и взя­тая с обратным знаком эта разность определяет вакуум: Р_в = — р — = р_а — р. Вакуум показывает, насколько абсолютное давление меньше атмосферного. Величина р_визмеряется вакуумметрами.

Пар называется насыщенным, когда число молекул, переходящих из жидкости в пар, равно числу молекул, совершающих обратный переход. В этом случае в паре устанавливается вполне определенное при данной температуре давление, называемое давлением насыщенного пара р_п.

Давление насыщенного пара р_п зависит от рода жидкости и от темпе­ратуры. Давления насыщенных паров воды, легкой нефти, бензина и глинистого раствора при разных температурах приведены в табл. 1.1.

Кипение в жидкости наступает, когда температура становится выше, чем температура кипения при данном давлении, или вследствие понижения давления до значений, меньших давления насыщенного пара при данной температуре. Кипение, возникающее в движущейся жидкости вследствие местных понижений давления до давления насыщенного пара, называется кавитацией.

Жидкость называется несжимаемой, если ее плотность не зависит от

давления, т.е. dr /dp = 0.

Если плотность жидкости изменяется в зависимости от давления, то величина

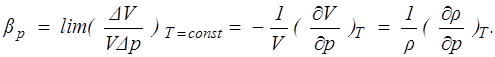(1.5)

называется коэффициентом сжимаемости. Он равен относительно­му изменению объема жидкости при изменении давления на одну едини­цу. Коэффициент сжимаемости имеет размерность, обратную давлению:

[b_p]_СИ= Па^-1 .

Таблица 1.1.

Давления насыщенных паров (Па) некоторых жидкостей

Жидкость	Температура, °С
Вода
Легкая нефть		—		—		—
Бензин
Глинистый раствор	—

Продолжение табл. 1.1

Жидкость	Температура, °С
Вода
Легкая нефть		—		—	—
Бензин	—	—	—	—	—
Глинистый раствор	—	—	—	—	—

Величина обратная коэффициенту сжимаемости, называется модулем объемной упругости жидкости

К= 1/b_r . (1.6)

Для воды среднее значение модуля объемной упругости К=2 ×10⁹ Па; Для керосина К=1,7 ×10⁹ Па ; для дизельного топлива К=1,6 ×10⁹ Па; для других нефтепродуктов К=1,3 ×10⁹ Па.

Плотность жидкости может изменяться при изменении температуры. В этом случае изменение плотности характеризуется коэффициентом теплового объемного расширения b_Т , определяемым по формуле

b_Т = lim­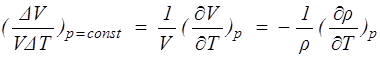 ,(1.7)

Коэфициент теплового объемного расширения b_Т равен относительному изменению объема жидкости при изменении температуры на один градус. Размерность b_Т обратна температуре

[b_Т] _СИ = градус^-1 .

Если известна плотность нефтепродуктов при 15 °С (r₁₅) , то величину r при другой температуре можно определить по формуле Менделеева:

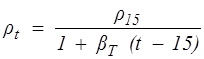, (1.8)

где t – температура нефтепродуктов, °С ; b_Т – коэффициент, зависящий от r₁₅ .

Значения коэффициента b_Т в формуле Менделеева приведены ниже:

r₁₅ , кг/м³ ……………… 700 800 850 900 920

b_Т × 10 ^–4,°С ……………… 8,2 7,7 7,2 6,4 6,0

В общем случае

.

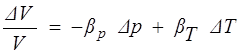Идеальная и вязкая жидкости. Существуют две распространенные модели жидкости. Первая из них предполагает, что в жидкости и при движении нет касательных напряжений. Это модель идеальной жидкости. Вторая модель учитывает при движении касательные напряжения. Это модель вязкой жидкости.

В простейшем случае прямолинейного слоистого течения связь между касательным напряжениям t и производной скорости u по нормали определяется законом вязкого трения Ньютона

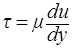. (1.9)

Коэффициент пропорциональности m в этой формуле называется динамическим коэффициентом вязкости. Этот коэффициент определяется свойствами жидкости и зависит от давления и температуры. Размерность динамического коэффициента вязкости

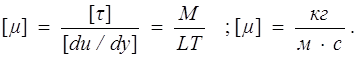
Для характеристики вязких жидкостей вводят еще один коэффициент – кинематический коэффициент вязкости v :

v=m /r

Физические свойства газа

Состояние однородного газа определяется тремя параметрами — абсолютным давлением р, плотностью r и абсолютной температурой Т, из которых только два являются независимыми. Уравнение Ф (р, r, Т) = 0, связывающее эти величины, называется уравнением сос­тояния.

Уравнение Клапейрона для массы газа т, занимающей объем V, имеет вид

pV= mRT, (1.10)

где R — газовая постоянная, измеряемая в СИ в Дж/ (кг • К). Уравнение (1.10) можно записать также в виде

p/r = RT. (1.11)

Уравнение Клапейрона для одного киломоля газа m записывается в виде

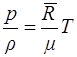, (1.12)

где 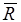— универсальная газовая постоянная, величина постоянная для всех газов и равная 8314 Дж/ (кмоль • К).

Для воздуха газовая постоянная равна

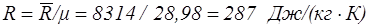. (1.13)

Удельный объем газа u и его плотность r связаны соотношением:

.

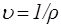Газ называется совершенным, если давление р, плотность r и абсолютная температура Т удовлетворяют уравнению Клапейрона (1.11) или (1.12) и удельную внутреннюю энергию газа U можно предс­тавить в виде

,

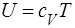где c_V — теплоемкость газа при постоянном объеме.

Для реальных углеводородных газов уравнение состояния представляется следующим образом:

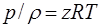(1.14)

или

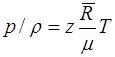. (1.15)

Здесь 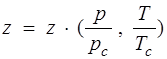; (1.16)

z — коэффициент сжимаемости; р_с, Т_с — критические давление и температура, т.е. давление и температура в критической точке.

Критической точкой называется точка на карте изотерм (диаг­рамме состояния р — V — Т) , в которой исчезает различие между насы­щенным паром и жидкостью. При температуре выше критической не существует двухфазных состояний. Вещество находится в однофазном состоянии.

Для природных углеводородных газов коэффициент сжимаемости определяется по экспериментальным кривым.

Система находится в термодинамическом равновесии, если пара­метры, определяющие ее состояние, остаются постоянными.

Обратимым процессом называется процесс изменения состояния системы, который, будучи проведен в обратном направлении, возвра­щает ее в исходное состояние через те же промежуточные состояния, и при этом в окружающей среде никаких изменений не происходит.

Обратимый процесс можно представить как непрерывную последо­вательность равновесных состояний, т.е. как квазистатический процесс. Только в том случае, когда реальный процесс может рассматриваться как квазистатический, при выводе формул, описывающих его, можно пользоваться уравнениями равновесного состояния (1.10) — (1.16).

Первое начало термодинамики выражает закон сохранения энер­гии в применении к преобразованиям механической энергии в тепло­вую и обратно. Для квазистатических процессов его можно сформули­ровать следующим образом: подведенное к единице массы газа элемен­тарное количество теплоты dQ расходуется на повышение внутренней энергии газа dU ина выполнение работы расширения pdu :

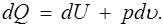(1.17)

Количество теплоты dQ, сообщенное газу, не является полным дифференциалом, так как зависит не только от начального и конечного состояния газа, но и от самого процесса изменения состояния. Если уравнение (1.17) умножить на интегрирующий множитель 1/Т, то по­лучим полный дифференциал некоторой функции, называемой энтро­пией:

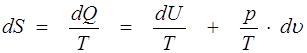. (1.18)

При переходе газа из состояния 1 в состояние 2 изменение энтропии S₂ — S₁ не зависит от процесса перехода, а определяется только началь­ным и конечным состояниями.

Для совершенного газа

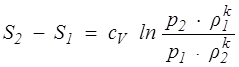, (1.19)

где k – с_p / c_V — показатель адиабаты Пуассона; с_р и с_V – теплоемкости газа при постоянном давлении и при постоянном объеме соответственно, отнесенные к единице массы. Они измеряются в СИ в Дж/(кг • К). Определенное по формуле (1.19) приращение энтропии тоже отнесено к единице массы.

Процесс, происходящий без теплообмена системы с окружающей средой, называется адиабатическим, а процесс, происходящий при постоянной энтропии, — изоэнтропическим. Изоэнтропический процесс описывается уравнением адиабаты Пуассона, которое получается из уравнения (1.19), если положить S₂ = S_l , т.е.

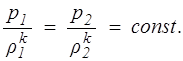(1.20)

Процесс, происходящий при постоянной температуре, называется изотермическим. Он описывается уравнением Бойля — Мариотта

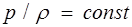. (1.21)

Энтальпией, отнесенной к единице массы (или теплосодержание при постоянном давлении), называется функция

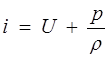, (1.22)

которая определяется только состоянием газа, например, его темпера­турой и давлением.

При адиабатическом течении реального газа через дроссель (вентиль, диафрагму и т.д.) из области большего давления p_i в область меньше­го давления p₂ наблюдается изменение температуры, вызванное изме­нением давления. Это явление называется эффектом Джоуля —Том­сона. Если за дросселем восстанавливается начальная скорость тече­ния газа, то энтальпия сохраняется неизменной:

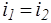(1.23)

или

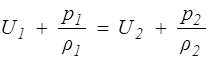. (1.24)

Температура в процессе Джоуля — Томсона может как повышаться, так и понижаться, в зависимости от характера сил взаимодействия между молекулами газа. Один и тот же газ при разных температурах может вести себя различно. Температура, при которой эффект меняет свой знак, называется точкой инверсии.

Дифференциальный эффект Джоуля — Томсона характеризуется коэффициентом Джоуля —Томсона

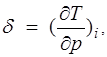(1.25)

зависящим от температуры и давления.

При дросселировании от высокого давления р₁ до значительно более низкого р₂ температура газа меняется на конечную величину T₁ — Т₂. Этот процесс принято называть интегральным эффектом Джоуля — Томсона. Для его характеристики вводится среднее значение коэффи­циента Джоуля — Томсона

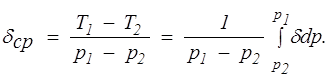
(1.26)

Для многих реальных газов составлены таблицы и построены графи­ки зависимости энтальпии от температуры и давления, диаг­рамма i — Т для метана. Эти графики могут служить для расчета эффек­та Джоуля — Томсона.

Для совершенного газа

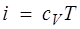, (1.27)

и изменение температуры за счет эффекта Джоуля — Томсона равно нулю.

Вопросы по теме 1.2.

1. Какой газ называется совершенным?

2. Какой процесс называется изоэнтропическим?

3. Как изменяется плотность совершенного газа при увеличении давления, если процесс изотермический?

4. Как зависит внутренняя энергия совершенного газа от темпе­ратуры?

5. Как записывается уравнение состояния реального газа?

Вопросы по теме 1.3.

1. Какие виды давления Вы знаете и какими приборами они изме­ряются?

2. Каково численное соотношение между единицами давления "паскаль" и "техническая атмосфера"?

3. Как запишется основное уравнение гидростатики, если известно р_И на свободной поверхности жидкости и требуется определить абсолют­ное давление в нижерасположенной точке?

4. Какой вид давления обязательно используется в формулах баро­метрической и барометрического нивелирования?

5. Где расположена пьезометрическая поверхность для открытого сосуда с жидкостью?

Вопросы по теме 1.4.

1. Как определяется равнодействующая сил давления на твердую поверхность и что понимается под символом р_T?

2. Может ли равнодействующая сил давления действовать с внешней стороны твердой поверхности, где жидкости нет?

3. Что такое центр давления?

4. Может ли центр давления располагаться выше центра тяжести смо­ченной части плоской поверхности?

Вопросы по теме 1.5.

1. В чем сходство и различие формул для определения горизонталь­ной составляющей силы давления жидкости на криволинейную поверх­ность и силы давления на плоскую поверхность?

2. Что называется "телом давления"?

3. Если в нижней точке криволинейной поверхности в жидкости, на­ходящейся над ней, вакуум, то как по отношению к этой поверхности располагается "тело давления" и каково направление вертикальной составляющей силы давления?

4. Если тело тонет, то куда направлена Архимедова сила?

Вопросы по теме 1.6.

1 . Какие силы действуют на жидкость при ее относительном покое?

2. Каковы форма изобарических поверхностей в жидкости и описы­вающее их уравнение при прямолинейном движении сосуда с постоян­ным ускорением?

3. Каковы форма изобарических поверхностей в жидкости и описы­вающее их уравнение при вращении сосуда с постоянной угловой ско­ростью и вертикальной осью вращения?

3. Каков закон распределения давления в жидкости по вертикали при ее относительном покое?

Основные понятия кинематики и динамики жидкости

Скорость частицы жидкости 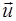зависит от координат х, у, z этой частицы и времени t, т.е.

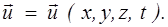
Плотность r и давление р также являются функциями координат и времени

r = r (x, y, z, t); p = p (x, у, z, t).

Если характеристики течения не зависят от времени, т.е. могут изме­няться лишь от точки к точке, то течение называется установившимся. Если в данной точке пространства характеристики течения изменяются со временем, то течение называется неустановившимся.

Линией тока называется линия, в каждой точке которой вектор скорости 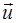направлен по касательной к этой линии. Уравнения для линий тока имеют вид

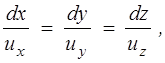(2.1)

где и_х, и_y , u_z — составляющие вектора скорости .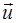

Совокупность линий тока, проходящих через замкнутый контур L, образует трубчатую поверхность — трубку тока. Жидкость, находя­щаяся внутри трубки тока, образует струйку. Если контур L мал, то трубка тока и струйка называются элементарными.

Сечение струйки s, нормальное в каждой своей точке к линиям то­ка, называется живым сечением.

Область пространства конечных размеров, занятая движущейся жидкостью, называется потоком. Поток обычно рассматривается как совокупность элементарных струек. Живое сечение потока определяется так же, как в случае элементарной струйки.

Гидравлический радиус R_г живого сечения определяется как отношение площади живого сечения s к смоченному периметру c, т.е.

R_г = s/c. (2.2)

Под смоченным периметром c понимается та часть геометри­ческого живого сечения, по которой жидкость соприкасается с твердыми стенками.

Если форма и площадь живого сечения по длине потока не изменяют­ся, то поток называется равномерным. В противном случае поток на­зывается неравномерным. В том случае, когда живое сечение плавно изменяется по длине, течение называется плавно изменяющимся.

В живом сечении 1 — 1 (рис. 2.1) равномерного потока выполняется гидростатический закон распределения давления, т.е.

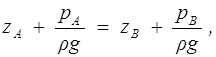(2.3)

где р_А, р_B — соответственно давления в произвольных точках А и В (с вертикальными координатами z_a, z_b) этого сечения; g — ускоре­ние свободного падения. В случае плавно изменяющегося течения ра­венство (2.3) выполняется приближенно.

Расходом жидкости через поверхность s называется количество жидкости, протекающей через эту поверхность _в единицу времени. Объемный расход Q, массовый расход Q_М > весовой расход q_G определяются по формулам

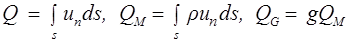, (2.4)

где и_n — проекция скорости 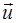на нормаль 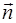к поверхности s.

Если s — живое сечение, то и_п = u. Для однородной жидкости

Q_m = rQ (2.5)

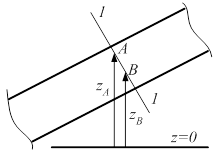Рис. 2.1. Живое сечение равномерного потока

Средняя скорость u определяется из равенства

u=Q/s. (2.6)

Уравнение неразрывности для потока несжимаемой жидкости имеет вид

Q = u ₁ s₁ = u₂s₂, (2.7)

где u ₁ , u₂ — средние скорости в сечениях 1 - 1 и 2 - 2.

Уравнение Бернулли для элементарной струйки вязкой несжимае­мой жидкости при установившемся движении в поле силы тяжести имеет вид

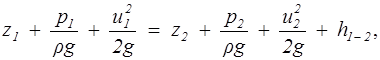(2.8)

где z₁, z₂ - расстояния от центров выбранных живых сечений 1 — 1 и 2 — 2 до некоторой произвольной горизонтальной плоскости z = 0 (рис. 2.2); u₁, u₂ - скорости; P₁,P₂ -давления в этих сечениях; h_1-2 — потери напора на участке между выбранными сечениями.

Уравнение Бернулли выражает собой закон сохранения механичес­кой энергии. Величина

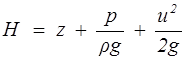(2.9)

называется полным напором и представляет собой удельную (прихо­дящуюся на единицу силы тяжести) механическую энергию жидкости в рассматриваемом сечении; z — геометрический напор или удельная потенциальная энергия положения; p/(rg) — пьезометрический напор или удельная потенциальная энергия давления; u²/(2g) - скоростной напор или удельная кинетическая энергия; h_1-2 — потери напора, т.е. часть удельной механической энергии, израсходованной на работу сил трения на участке между сечениями 1 — 1 и 2 — 2 (см. рис. 2.2).

В случае идеальной жидкости h_1-2 =0.

Для плавно изменяющегося потока при установившемся движении вязкой несжимаемой жидкости в поле силы тяжести уравнение Бернул­ли имеет вид

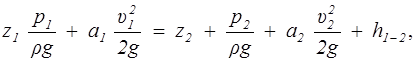(2.10)

где p₁, p₂ — давления в произвольно взятых точках сечений 1 — 1 и 2 — 2 скоординатами z₁ и z₂ соответственно (обычно берутся точки на оси потока); u ₁ , u₂ — средние скорости в этих сечениях; а₁ , а₂ — коэффи­циенты Кориолиса, учитывающие неравномерность распределения ско­ростей частиц жидкости в сечениях; при течении по круглой цилиндри­ческой трубке a = 2 для ламинарного режима течения и a » 1,1 — для турбулентного; при решении практических задач обычно принимается a = 1.

При использовании уравнения Бернулли (2.8) или (2.10) необходи­мо иметь в виду, что номера сечений возрастают в направлении течения жидкости. В качестве расчетных выбираются такие сечения (струйки) , в которых известны какие-либо из величин u ₁ , u₂ (u₁, u₂) и р₁, р₂ .

Плоскость z = 0 бывает удобно располагать таким образом, чтобы центр одного из выбранных сечений потока лежал в этой плоскости.

Потери напора h_1-2 , отнесенные к единице длины трубопровода, называются гидравлическим уклоном:

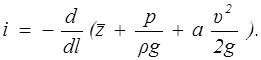(2.11)

В случае равномерного движения несжимаемой жидкости

i = h_l-2 / l, (2.12)

где l — расстояние между выбранными сечениями.

При движении жидкости по трубопроводу различают два вида потерь напора: потери по длине трубопровода h_д и потери в местных сопротив­лениях h_м . К потерям по длине относят потери на прямолинейных участ­ках трубопровода, а к потерям на местных сопротивлениях — потери на таких участках трубопровода, где нарушается нормальная конфигурация потока (внезапное расширение, поворот, запорная арматура и т.д.) .

Вопросы по теме 2.

1. Что называется линией тока?

2. Может ли жидкость протекать сквозь боковую поверхность труб­ки тока?

3. Что называется живым сечением потока?

4. Чем отличается уравнение Бернулли для струйки тока от уравне­ния Бернулли для потока?

5. Что такое гидравлический уклон?

6. Как определяется средняя скорость потока?

7. Какая связь между объемным, массовым и весовым расходами?

8. Как изменяются по длине неравномерного потока несжимаемой жидкости расход и средняя скорость?

Вопросы по теме 3.

1 . Что такое параметры с независимыми размерностями?

2. Чему равно максимально возможное число параметров с незави­симыми размерностями?

3. В чем заключаются условия подобия двух явлений?

4. Какой вид примет формула (3.3) при n = k?

5. Как вычислить число Рейнольдса для некруглой трубы?

Вопросы по теме 4.

1. Как записать закон сохранения массы при установившемся тече­нии газа в трубке тока?

2. Что понимается под параметрами торможения газа?

3. Как изменяются параметры торможения по длине потока при адиабатическом, изэнтропическом течении газа в трубке тока?

4. Что происходит с температурой идеального совершенного газа с ростом скорости при установившемся адиабатическом течении в трубке тока?

Вопросы по теме 5.

1 . По каким формулам определяются потери напора в трубах по длине и в местных сопротивлениях?

2. От каких безразмерных величин может зависеть коэффициент гидравлического сопротивления?

3. Каковы границы зон сопротивления при турбулентном течении?

4. Что такое эквивалентная и приведенная длины и когда они упот­ребляются?

Рис. 6.2. Гидравлическая характеристика простого трубопровода

При решении задачи любого типа может оказаться, что в каком-либо сечении трубопровода давление в жидкости окажется меньше (или равным) давления насыщенных ее паров p_п при данной температуре. В этом случае жидкость вскипает и образуются полости, заполненные парами. Сплошность потока нарушается. Такое явление называется кавитацией. Для его предотвращения в трубопроводах, работающих или при давлении ниже атмосферного (сифонные сливы, всасывающие линии насосных установок), или транспортирующих сжиженные газы, необходимо поддерживать условие р > р_пдля любого живого сечения, где под р понимается абсолютное давление. Проверка выполнения это­го условия обычно проводится для "опасного" сечения, т.е. сечения, в котором давление наименьшее.

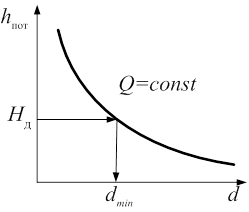
Рис. 6.3. Графическая зависимость потерь напора в простом трубопроводе от диаметра

Вопросы по теме 6.

1. Какие три основные задачи рассматриваются при расчете трубо­проводов?

2. В чем заключается сущность графоаналитического метода расчета трубопроводов и какие задачи им решаются?

3. Какие признаки позволяют предположить ламинарное движение жидкости или квадратичную зону гидравлического сопротивления?

4. Что называется гидравлической характеристикой трубопроводов и каков принцип ее построения?

5. Каково дополнительное условие работы трубопроводов, если они работают при давлении ниже атмосферного?

6. Какое живое сечение трубопровода называется опасным?

Вопросы по теме 7.

1.Какие трубопроводы называются сложными?

2.Как связаны между собой расходы и потери напора на участках с общими расходами и потерями напора на всем трубопроводе при после­довательном и параллельном соединении участков?

3.Как строятся гидравлические характеристики для всего трубо­провода, если его участки соединены или последовательно, или парал­лельно?

4.Как влияет на потери напора в трубопроводе подсоединенный к нему лупинг?

5.В чем заключается метод определения диаметров участков раз­ветвленного трубопровода, если известны требуемые в ветвях расходы?

Рис. 8.2. Схема истечения жидкости через затопленное малое отверстие

При истечении через большое прямоугольное отверстие (рис. 8.3), размеры которого а х b имеют тот же порядок, что и глубина погру­жения его центра Н, расход определяется по формуле

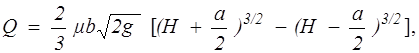(8.13)

где b —ширина отверстия.

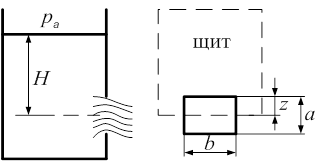
Рис. 8.6. Схема истечения жидкости из резервуара при переменном уровне

Если площадь сечения резервуара S_p переменна по высоте, то время снижения уровня от Н₁ до Н₂ можно найти из соотношения

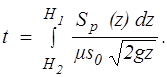(8.19)

Для цилиндрического резервуара (S_P = const)

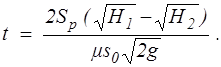(8.20)

Время полного опорожнения горизонтальной цилиндрической цис­терны, в начальный момент доверху заполненной жидкостью, опреде­ляется по формуле

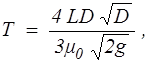(8.21)

где L - длина цистерны; D - ее внутренний диаметр,

Вопросы по теме 8.

1. В каком случае отверстие в стенке бака, из которого происходит истечение, называется малым?

2. Как определяются коэффициенты истечения (сжатия струи, скорости, расхода) ?

3. Как найти среднюю скорость в сжатом сечении струи и расход при истечении жидкости через малое отверстие при постоянном напоре?

4. Как определяется расход жидкости при истечении через затоплен­ное отверстие?

5. Что называется насадками?

6. Каковы простейшие типы насадков и их характеристики?

7. Какое давление возникает внутри цилиндрического насадка при истечении в атмосферу? Каково условие нормальной работы насадка?

8. Как найти время полного опорожнения вертикального цилиндри­ческого резервуара?

Вопросы по теме 9.

1. Чему равна скорость распространения волны гидравлического удара в случае недеформируемых стенок трубопровода (Е = ¥ ) ?

2. Как надо закрывать задвижку в трубопроводе, чтобы уменьшить давление, возникающее при гидравлическом ударе, — быстро или мед­ленно?

3. Ударное повышение давления больше при прямом или непрямом гидравлическом ударе?

4. Что будет происходить с ударным давлением при увеличении упру­гости стенок трубопровода?

5. Как будет изменяться ударное давление при увеличении диаметра трубы и сохранении толщины ее стенки?

Рис. 10.1. Кривые течения неньютоновских вязких жидкостей

На рис. 10.1 приведены кривые течения неньютоновских вязких жидкостей. Кривая 1 соответствует вязкопластичной жидкости, кривая 2 —псевдопластичной, кривая 4 —дилатантной; кривая 3 соответствует случаю п = 1, т.е. представляет собой кривую течения для вязкой жид­кости.

Для неньютоновских вязких жидкостей вводится понятие кажу­щейся вязкости

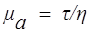(10.5)

и текучести

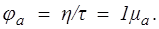(10.6)

В отличие от ньютоновской жидкости величины m_а и j_а — не конс­танты, а функции касательного напряжения.

При движении неньютоновской вязкой жидкости по трубе радиусом а и длиной l под действием перепада давления Dp распределение каса­тельного напряжения по радиусу, как и в случае ньютоновской жидкос­ти, имеет вид

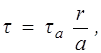(10.7)

где t_а — касательное напряжение на стенке трубы, определяемое из соотношения:

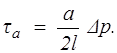
Распределение скорости по сечению трубы определяется по формуле

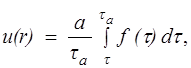(10.8)

где f(t) определяется по формуле (10.3).

Расход неньютоновской вязкой жидкости определяется при любом виде функции f(t) из соотношения

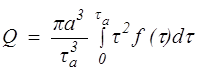. (10.9)

Формулы (10.6) и (10.7) справедливы при отсутствии пристенного скольжения. При вращательном течении неньютоновской вязкой жид­кости между двумя соосными цилиндрами распределение касательного напряжения по радиусу имеет вид

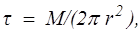(10.10)

где М — момент сил трения, действующих на единицу длины цилиндра.

Угловая скорость наружного цилиндра W при отсутствии пристен­ного скольжения и неподвижном внутреннем цилиндре определяется по формуле

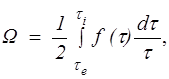(10.11)

где t_i , t_e — напряжения сил трения на поверхностях внутреннего и наружного цилиндра соответственно.

Вопросы по теме 10.

1. Как определяется неньютоновская жидк