Описание прибора и практическая часть работы.

Цель работы.

Изучение колебательных движений маятников. Измерение ускорения свободного падения.

Оборудование.

1. Универсальный маятник FPM-04

Темы для изучения.

В лабораторной работе рассмотрены основные понятия и законы, на которых основан принцип действия математического и оборотного маятников, получена рабочая формула для определения ускорения си­лы тяжести при помощи математического и оборотного маятников, проведено описание экспериментальной установки и порядка работы на ней.

Лабораторная работа предназначена для студентов, выполняющих общий физический практикум в лаборатории механики кафедры экспе­риментальной физики ТГУ.

Краткая теория.

Ускорение свободного падения относительно Земли в разных точках земного шара различно. Это обусловлено неинерциальностью системы отсчета, связанной с Землей, и изменением силы гравитационного вза­имодействия рассматриваемого тела с Землей в различных ее точках.

Поэтому измерение ускорения свободного падения в различных точках Земли с одной стороны дает указания о форме Земли, а с дру­гой стороны позволяет обнаруживать различные местные неоднороднос­ти в строении земного шара.

Одним из методов достаточно точного определения ускорения сво­бодного падения является исследование колебательного движения маят­ников.

В физике под маятником понимают твердое тело, совершающее под действием силы тяжести колебательное движение относительно непод­вижной оси. Различают математический и физический маятники.

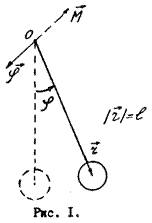
Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке. Достаточно хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити (рис.1).

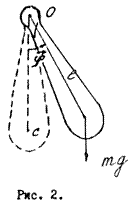
Физическим маятником называют твердое те­ло, закрепленное на горизонтальной оси, проходящей через точку О расположенную выше его центра тяжести С (рис. 2).

Рассмотрим динамику движения этих маятников.

При отклонении маятников на угол 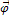из

положения равновесия возникает вращательный момент 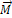относительно точки О. В дан­ном случае на тело действуют только моменты силы тяжести, так как момент силы реакции оси равен нулю. Известно, что сумма моментов сил тяжести равна моменту равнодействующей силы 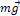, при усло­вии, что она приложена к центру тяжести, В однородном поле центр тяже­сти совпадает с центром масс тела.

По определению момент силы 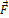относительно точки O: 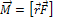, где 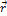- радиус-вектор точки приложены силы относительно точки О.

Уравнением движения тела, закрепленного на неподвижной оси, явля­ется основное уравнение динамики вращательного движения, имеющее вид:

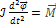(1)

где ℐ - момент инерции тела относительно оси; 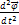- угловое ускорение. .

Под вектором угла 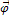понимается вектор, по модулю равный 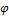и направленный вдоль оси вращения таким образом, чтобы с его начала

ЛАБОРАТОРНАЯ РАБОТА. ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ ПРИ ПОМОЩИ МАТЕМАТИЧЕСКОГО И ОБОРОТНОГО МАЯТНИКОВ

поворот наблюдался происходящим по часовой стрелке.

По определению векторного произведения момент силы тяжести будет в данном случае направлен противоположно направлению .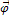

Для решения дифференциального уравнения (1) перейдем от век­торной формы к скалярной. Рассмотрим проекции векторов 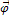и 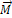на ось координат, совпадающую с осью вращения и направленную по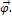

Составляющая момента силы 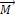относительно точки О вдоль оси, проходящей через эту точку, называется моментом силы относительно оси.

Вектор 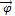можно записать следующим образом:

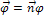, где 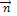- единичный вектор, направленный вдоль 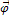, а 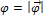, тогда угловое ускорение 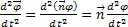, так как направление вектора 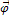не меняется со временем.

Таким образом, уравнение (1) в проекции на выбранную коорди­натную ось запишется:

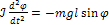(2)

Поскольку 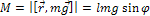, где .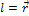
Знак (-)_, как уже говорилось, учитывает то обстоятельство, что 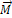направлен противоположно . •

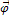Если ограничиться случаем малых отклонений из положения рав­новесия, то можно считать .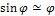

Уравнение (2) при этом переходит в уравнение:

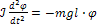(3)

или

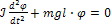(4)

Поделив обе части уравнения (4) на ℐ, подучим уравнение, опи­сывающее гармонические колебания:

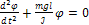(5)

Общим решением уравнения (5) будет функция вида:

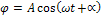(6) (б)

где A и ∝ - произвольные постоянные, определяемые на началь­ных условий, a

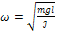- циклическая частота колебаний.

Поскольку период колебаний и циклическая частота связаны со­отношением 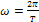можем определить период рассматриваемых гармонических колебаний:

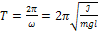(7)

Из (7) получаем непосредственно выражение для ускорения сво­бодного падения

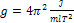(8)

Таким образом, зная период колебаний маятника и его момент инерции» можно определить ускорение свободного падения. Для математического маятника момент инерции .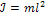

Следовательно, ускорение свободного падения при помощи коле­баний математического маятника можно определить по формуле:

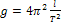(9)

Формула (9) является формулой для расчета ускорения свободного па­дения при колебаниях математичес­кого маятника.

Для физического маятника появляются трудности с определением момента инерции ℐ, который трудно вычислить с большой степенью точности. Поэтому для измерения g описанным способом использу­ются маятники особой конструкции, которые позволяют либо легко вы­числять момент инерция, либо исключить его из рассмотрения.

В данной работе используется так называемый оборотный маят­ник, конструкция которого позволяет исключить момент инерции на рассмотрения.

Получение рабочей формулы для определения g с помощью оборотного маятника.

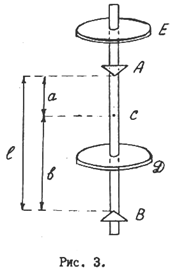
Оборотный маятник (рис. 3) состоит из длинного цилиндрического стержня, на котором закрепляются две подвижные призмы A и B и два подвижных тяжелых диска E и D.

Колебания маятника осуществляют­ся поочередно вокруг осей, про­ходящих через

ЛАБОРАТОРНАЯ РАБОТА. ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ ПРИ ПОМОЩИ МАТЕМАТИЧЕСКОГО И ОБОРОТНОГО МАЯТНИКОВ

ребра призм A и B. Обозначим расстояние от ребра призмы A до центра масс С через a; расстояние от ребра призмы В до центра масс С - через b ; расстояние между ребрами призм - l.

Пусть 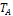и 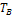периоды колебаний маятника относительно осей, проходящих соответственно через ребра призм A и В.

В соответствии с формулой (7) можно записать:

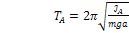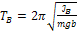; , (10)

где 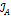и 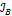- моменты инерции маятника относительно осей, проходящих через соответствующие ребра призм.

Возведем каждое из выражений (10) в квадрат, домножим первое на a, второе - на b и вычтем друг из друга:

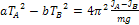(11)

Моменты инерци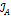и и 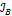можно определить, воспользовав­шись теоремой Штейнера: момент инерции тела относительно оси, не проходящей через центр масс, равен сумме двух слагаемых: момента инерции относительно параллельной ей оси, проходящей через центр масс JЈ и произведе­ния кассы тела на квадрат расстояния между центром масс и рассмат­риваемой осью.

Таким образом:

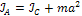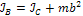; (12)

Подставив соотношения (12) в (11), получим:

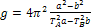(13)

Если подобрать положения дисков E и D таким образом, чтобы выполнялось соотношение 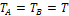, то формула (13) значительно упрощается и мы получим рабочую фор­мулу для определения ускорения си­лы тяжести при помощи оборотного маятника.

,

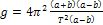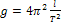, (14)

где l - расстояние между ребрами призм в случае равенства пе­риодов колебаний относительно каждого из ребер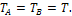

Правила безопасности.

Эксплуатация прибора допускается только при наличии заземления.

Выполнение работы.

Цель работы.

Изучение колебательных движений маятников. Измерение ускорения свободного падения.

Оборудование.

1. Универсальный маятник FPM-04

Темы для изучения.

В лабораторной работе рассмотрены основные понятия и законы, на которых основан принцип действия математического и оборотного маятников, получена рабочая формула для определения ускорения си­лы тяжести при помощи математического и оборотного маятников, проведено описание экспериментальной установки и порядка работы на ней.

Лабораторная работа предназначена для студентов, выполняющих общий физический практикум в лаборатории механики кафедры экспе­риментальной физики ТГУ.

Краткая теория.

Ускорение свободного падения относительно Земли в разных точках земного шара различно. Это обусловлено неинерциальностью системы отсчета, связанной с Землей, и изменением силы гравитационного вза­имодействия рассматриваемого тела с Землей в различных ее точках.

Поэтому измерение ускорения свободного падения в различных точках Земли с одной стороны дает указания о форме Земли, а с дру­гой стороны позволяет обнаруживать различные местные неоднороднос­ти в строении земного шара.

Одним из методов достаточно точного определения ускорения сво­бодного падения является исследование колебательного движения маят­ников.

В физике под маятником понимают твердое тело, совершающее под действием силы тяжести колебательное движение относительно непод­вижной оси. Различают математический и физический маятники.

Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке. Достаточно хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити (рис.1).

Физическим маятником называют твердое те­ло, закрепленное на горизонтальной оси, проходящей через точку О расположенную выше его центра тяжести С (рис. 2).

Рассмотрим динамику движения этих маятников.

При отклонении маятников на угол 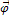из

положения равновесия возникает вращательный момент 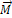относительно точки О. В дан­ном случае на тело действуют только моменты силы тяжести, так как момент силы реакции оси равен нулю. Известно, что сумма моментов сил тяжести равна моменту равнодействующей силы 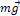, при усло­вии, что она приложена к центру тяжести, В однородном поле центр тяже­сти совпадает с центром масс тела.

По определению момент силы 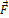относительно точки O: 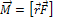, где 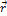- радиус-вектор точки приложены силы относительно точки О.

Уравнением движения тела, закрепленного на неподвижной оси, явля­ется основное уравнение динамики вращательного движения, имеющее вид:

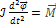(1)

где ℐ - момент инерции тела относительно оси; 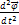- угловое ускорение. .

Под вектором угла 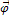понимается вектор, по модулю равный 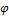и направленный вдоль оси вращения таким образом, чтобы с его начала

ЛАБОРАТОРНАЯ РАБОТА. ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ ПРИ ПОМОЩИ МАТЕМАТИЧЕСКОГО И ОБОРОТНОГО МАЯТНИКОВ

поворот наблюдался происходящим по часовой стрелке.

По определению векторного произведения момент силы тяжести будет в данном случае направлен противоположно направлению .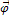

Для решения дифференциального уравнения (1) перейдем от век­торной формы к скалярной. Рассмотрим проекции векторов 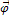и 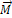на ось координат, совпадающую с осью вращения и направленную по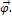

Составляющая момента силы 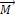относительно точки О вдоль оси, проходящей через эту точку, называется моментом силы относительно оси.

Вектор 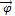можно записать следующим образом:

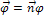, где 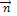- единичный вектор, направленный вдоль 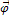, а 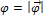, тогда угловое ускорение 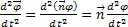, так как направление вектора 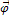не меняется со временем.

Таким образом, уравнение (1) в проекции на выбранную коорди­натную ось запишется:

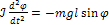(2)

Поскольку 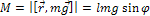, где .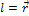
Знак (-)_, как уже говорилось, учитывает то обстоятельство, что 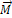направлен противоположно . •

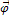Если ограничиться случаем малых отклонений из положения рав­новесия, то можно считать .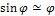

Уравнение (2) при этом переходит в уравнение:

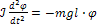(3)

или

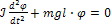(4)

Поделив обе части уравнения (4) на ℐ, подучим уравнение, опи­сывающее гармонические колебания:

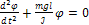(5)

Общим решением уравнения (5) будет функция вида:

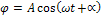(6) (б)

где A и ∝ - произвольные постоянные, определяемые на началь­ных условий, a

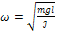- циклическая частота колебаний.

Поскольку период колебаний и циклическая частота связаны со­отношением 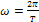можем определить период рассматриваемых гармонических колебаний:

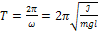(7)

Из (7) получаем непосредственно выражение для ускорения сво­бодного падения

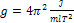(8)

Таким образом, зная период колебаний маятника и его момент инерции» можно определить ускорение свободного падения. Для математического маятника момент инерции .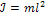

Следовательно, ускорение свободного падения при помощи коле­баний математического маятника можно определить по формуле:

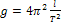(9)

Формула (9) является формулой для расчета ускорения свободного па­дения при колебаниях математичес­кого маятника.

Для физического маятника появляются трудности с определением момента инерции ℐ, который трудно вычислить с большой степенью точности. Поэтому для измерения g описанным способом использу­ются маятники особой конструкции, которые позволяют либо легко вы­числять момент инерция, либо исключить его из рассмотрения.

В данной работе используется так называемый оборотный маят­ник, конструкция которого позволяет исключить момент инерции на рассмотрения.

Получение рабочей формулы для определения g с помощью оборотного маятника.

Оборотный маятник (рис. 3) состоит из длинного цилиндрического стержня, на котором закрепляются две подвижные призмы A и B и два подвижных тяжелых диска E и D.

Колебания маятника осуществляют­ся поочередно вокруг осей, про­ходящих через

ЛАБОРАТОРНАЯ РАБОТА. ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ ПРИ ПОМОЩИ МАТЕМАТИЧЕСКОГО И ОБОРОТНОГО МАЯТНИКОВ

ребра призм A и B. Обозначим расстояние от ребра призмы A до центра масс С через a; расстояние от ребра призмы В до центра масс С - через b ; расстояние между ребрами призм - l.

Пусть 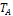и 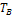периоды колебаний маятника относительно осей, проходящих соответственно через ребра призм A и В.

В соответствии с формулой (7) можно записать:

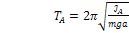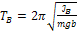; , (10)

где 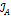и 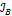- моменты инерции маятника относительно осей, проходящих через соответствующие ребра призм.

Возведем каждое из выражений (10) в квадрат, домножим первое на a, второе - на b и вычтем друг из друга:

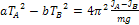(11)

Моменты инерци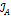и и 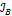можно определить, воспользовав­шись теоремой Штейнера: момент инерции тела относительно оси, не проходящей через центр масс, равен сумме двух слагаемых: момента инерции относительно параллельной ей оси, проходящей через центр масс JЈ и произведе­ния кассы тела на квадрат расстояния между центром масс и рассмат­риваемой осью.

Таким образом:

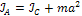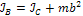; (12)

Подставив соотношения (12) в (11), получим:

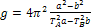(13)

Если подобрать положения дисков E и D таким образом, чтобы выполнялось соотношение 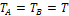, то формула (13) значительно упрощается и мы получим рабочую фор­мулу для определения ускорения си­лы тяжести при помощи оборотного маятника.

,

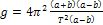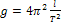, (14)

где l - расстояние между ребрами призм в случае равенства пе­риодов колебаний относительно каждого из ребер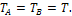

Описание прибора и практическая часть работы.

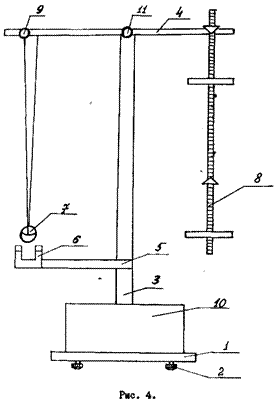
Общий вид универсального маятника FPM-04 представлен на рис. 4. Основание (1) оснащено регулируемыми ножками (2), которые позволя­ют произвести выравнивание прибора.

В основании закреплена колонка (3), на которой фиксируются верхний кронштейн (4) и нижний кронштейн (5) с фотоэлектрическим датчиком (6). После отвинчивания воротка (11)

верхний кронштейн мож­но поворачивать вокруг колонки. Закрепление воротка (11) фиксирует кронштейн в любом произвольно избранном положении. С одной сторо­ны кронштейна (4) находится математический маятник (7), с другой на вмонтированных вкладышах - оборотный маятник (8).

Длину математического маятника можно регулировать при помощи воротка (9), а ее величину можно определить при помощи шкалы на колонке (3).

Оборотный маятник выполнен в виде стального стержня, на кото­ром фиксируются два повернутые друг к другу лезвиями ножа и два тяжелых диска. На стержне через 10 мм выполнены кольцевые нарезки, служащие для точного определения длины оборотного маятника (расстояния между лезвиями ножей). Ножи и диски можно перемещать таким образом, что их размер вдоль стержня является кратным 10 мм, а фиксирующие воротки размещены так, чтобы при помощи кольцевых на­резок можно было их наглухо блокировать.

Нижний кронштейн вместе с фотоэлектрическим датчиком можно перемещать вдоль колонки и фиксировать в произвольно избранном по­ложении.

Фотоэлектрический датчик соединен с привинченным к основанию миллисекундомером FPM-I4 (10). На рис. 5

ЛАБОРАТОРНАЯ РАБОТА. ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ ПРИ ПОМОЩИ МАТЕМАТИЧЕСКОГО И ОБОРОТНОГО МАЯТНИКОВ

изображена лицевая панель миллисекундомера. На табло (12) в процессе работы высвечивается число периодов, а на табло (13) - полное время. В нижней части па­нели расположены клавиши; "сеть" (14); "сброс" (15) и "стоп"(16).

Прибор готов к работе непосредственно после включения в сеть и не нуждается в прогреве.

Правила безопасности.

Эксплуатация прибора допускается только при наличии заземления.

Выполнение работы.