Раздел 5. «Квантовая механика»

5.1. Квантовые свойства света.Проблема теплового излучения. Формула Планка. Фотоэффект. Эффект Комптона. Световое давление. Опыт Лебедева. Корпускулярно-волновой дуализм электромагнитного излучения.

5.2. Волновые свойства вещества.Дифракция электронов. Корпускулярно-волновой дуализм свойств вещества. Формула де Бройля. Принцип и соотношение неопределенностей Гейзенберга.

5.3. Квантово-механическое описание.Волна де Бройля. Квантовые состояния. Принцип суперпозиции. Уравнение Шредингера. Стационарные решения. Частица в потенциальной яме. Квантовый осциллятор. Операторы физических величин. Опыт Штерна – Герлаха. Момент импульса. Магнитный момент. Спин.

5.4. Атомы и молекулы в квантовой механике. Описание состояния атома. Энергетический спектр. Квантовые числа. Принцип запрета Паули. Таблица Менделеева. Молекулы. Природа химической связи.

5.5. Элементарные частицы и фундаментальные взаимодействия.Ядерная модель атома. Протоны, нейтроны и кварки. Адроны и
лептоны. Фундаментальные взаимодействия. Частицы – переносчики взаимодействий.

Раздел 6. «Термодинамика»

6.1. Термодинамическое описание состояния системы. Термодинамическая система. Параметры состояния. Уравнение состояния. Изопроцессы.

6.2. Первое начало термодинамики. Работа. Внутренняя энергия. Теплота. Первое начало термодинамики. Адиабатный процесс. Политропный процесс.

6.3. Второе начало термодинамики.Тепловые машины. Цикл Карно. Формула Карно. Второе начало термодинамики по Кельвину и по Клаузиусу. Приведенная теплота. Интеграл Клаузиуса. Энтропия. Неравновесные системы. Необратимость. Неравенство Клаузиуса. Энтропия и второе начало термодинамики. Третье начало термодинамики. Термодинамические функции состояния. Фазовые превращения и фазовое равновесие. Элементы неравновесной термодинамики.

6.4. Реальные газы.Уравнение Ван-дер-Ваальса. Изотермы Эндрюса. Пары. Влажность.

Раздел 7. «Статистическая физика»

7.1. Молекулярно-кинетическая теория. Основное уравнение МКТ. Связь энергии и температуры. Закон равнораспределения энергии по степеням свободы. Явления переноса. Диффузия. Вязкость. Теплопроводность.

7.2. Распределения Больцмана и Максвелла. Барометрическая формула. Распределение Больцмана. Распределение молекул по скоростям. Функция распределения. Распределение Максвелла. Наиболее вероятная скорость. Среднеарифметическая скорость.

7.3. Квантовые и классические распределения.Постановка задачи в классической статистике. Микро- и макросостояния. Термодинамическая вероятность. Статистическое истолкование энтропии. Формула Больцмана. Распределение Больцмана. Квантовая статистика. Распределение Ферми – Дирака. Распределение Бозе – Эйнштейна.

Раздел 8. «Физика конденсированного состояния»

8.1. Тепловые свойства твердых тел. Классическая теория теплоемкостей. Закон Дюлонга-Пти. Теория Эйнштейна. Теория Дебая. Формула Дебая.

8.2. Электрические свойства твердых тел. Классическая теория электропроводности. Зонная теория. Проводники, диэлектрики и полупроводники с точки зрения зонной теории. Проводимость полупроводников. Р-n переход. Полупроводниковый диод. Понятие о нанотехнологиях.

2. Пример оформления контрольной работы

ВАРИАНТ 1

Задача № 1

В подвешенный на нити длиной 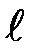= 1,8 м деревянный шар массой m = 8 кг попадает горизонтально летящая пуля массой m₁ = 4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в ней пулей отклонилась от вертикали на угол a = 3°? Размером шара пренебречь. Удар пули считать прямым центральным.

Дано: 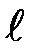= 1,8 м m2 = 8 кг m1 = 4 г = 0,004 кг a = 3° g = 9,8 м/с2	Решение:
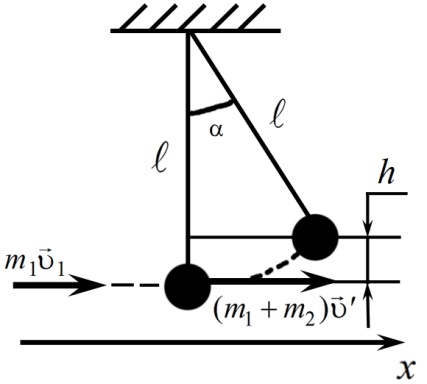u1 – ?

Запишем закон сохранения импульса для системы тел «Пуля и шар»:

,

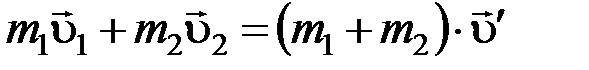где 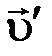– общая скорость шара и пули после неупругого удара.

В проекции на ось x имеем:

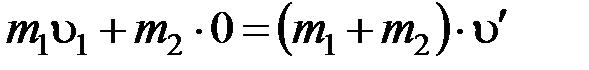. (1)

Из уравнения (1) выразим u₁:

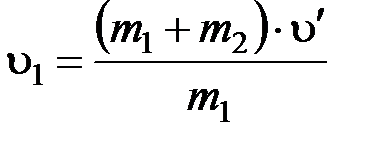. (2)

Запишем закон сохранения энергии для системы тел после неупругого соударения (полная механическая энергия остается величиной постоянной):

.

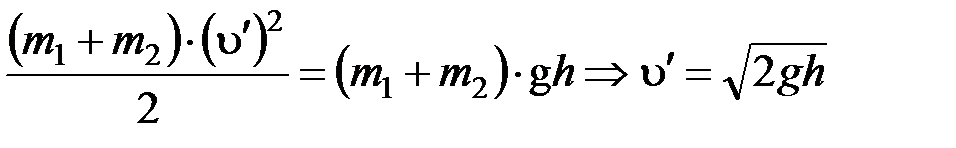Из рисунка видно, что:

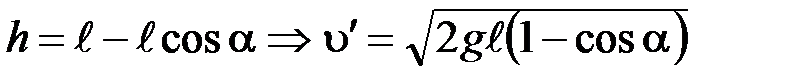. (3)

Подставляя (3) в (2), получаем:

.

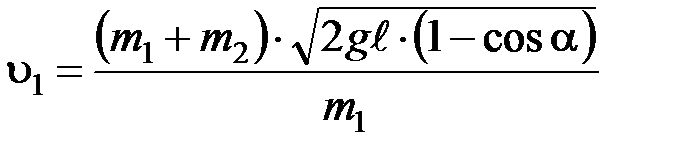Проверка размерности:

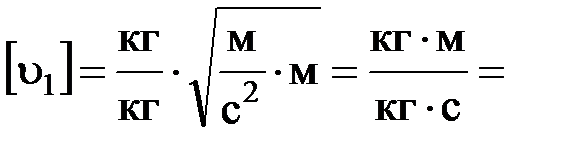м/с.

Расчет:

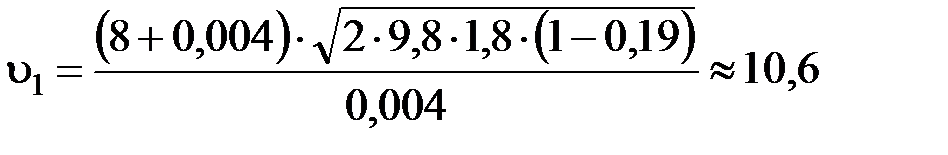(м/с)

Ответ: u₁ » 10,6 м/с.

Задача № 2

Смесь водорода и азота общей массой m = 290 г при температуре T =600 К и давлении p = 2,46 МПа занимает объем V = 30 л. Определить массу m₁ водорода и массу m₂ азота.

Дано: m = 290 г = 0,29 кг T =600 К = 6×102 К p = 2,46 МПа = 2,46×106 Па V = 30 л = 3×10 – 2 м3 m1 = 2×10 – 3 кг/моль m2 = 28×10 – 3 кг/моль

m1 (H2) – ? m2 (N2) – ?

Решение:

Согласно Закону Дальтона, давление смеси газов равно сумме парциальных давлений компонентов:

p = p₁ + p₂. (1)

Для определения парциальных давлений запишем уравнение Менделеева – Клапейрона для каждого компонента:

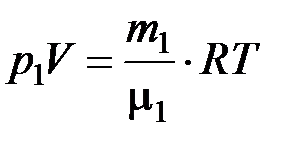, (2)

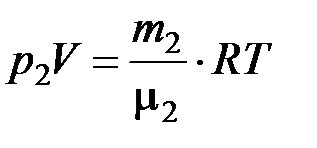, (3)

где индексом «1» отмечены характеристики, относящиеся к водороду, а индексом «2» – к азоту. Выразим p₁ и p₂ из уравнений (2) и (3) и подставим в закон Дальтона (1):

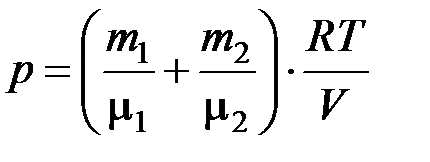; (4)

при этом m₁ + m₂ = m. (5)

Из (4) и (5) следует

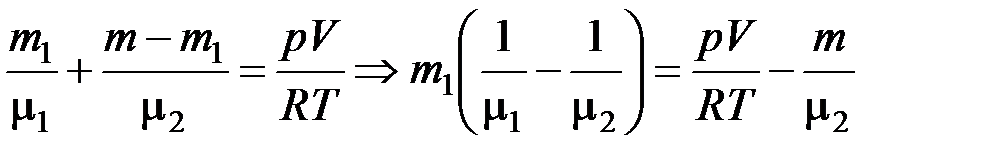. (6)

Из (6) получаем

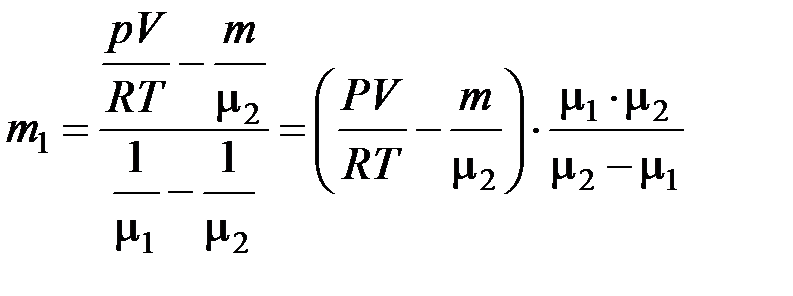. (7)

И далее находим массу азота:

m₂ = m - m₁.

Проверка размерности:

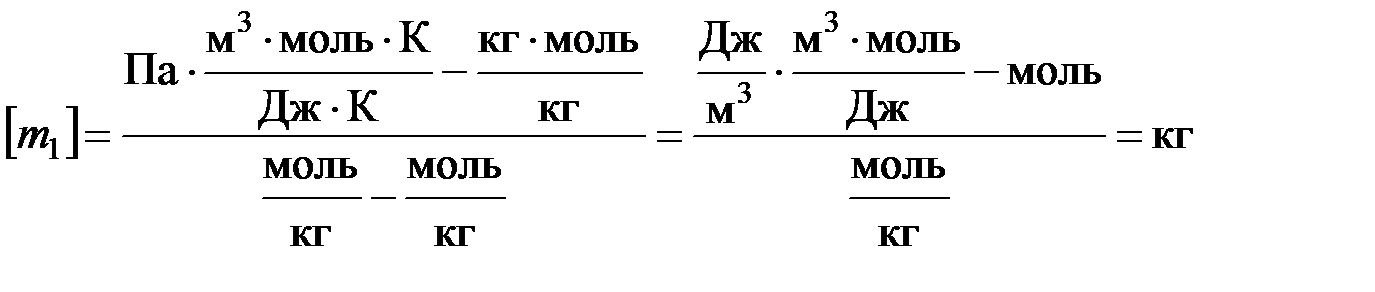
Расчет:

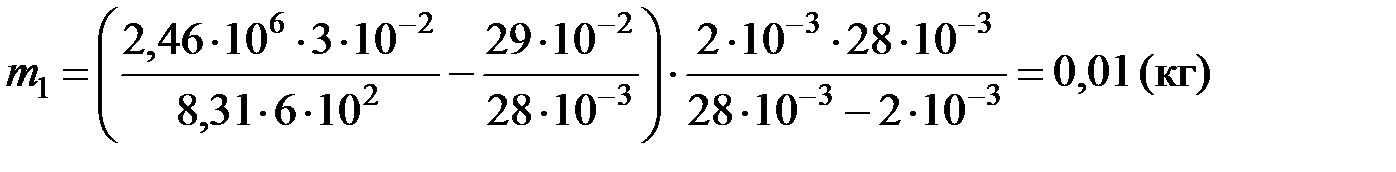
m₂ = 29×10 ^{– 2} - 1×10 ^{– 2} = 0,28 (кг)

Ответ:m₁ = 0,01 кг, m₂ = 0,28 кг.

Задача № 3

Две a-частицы, находясь первоначально достаточно далеко друг от друга, движутся по одной прямой навстречу одна другой со скоростями u и 2 u соответственно. На какое наименьшее расстояние они могут сблизиться?

Дано: m1 = m2 = m = 6,8×10 – 27 кг q1 = q2 = q = 3,2×10 – 19 Кл u1 = u u2 = 2 u

rmin – ?

Решение:

Расстояние между частицами будет минимальным, когда их относительные скорости, т. е. скорости сближения, станут равны нулю. В этом случае они будут двигаться с одинаковыми скоростями.

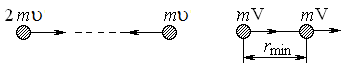
По закону сохранения импульса

2×m u - m u = 2 m V,

V = u / 2.

По закону сохранения энергии полная механическая энергия частиц сохраняется:

,

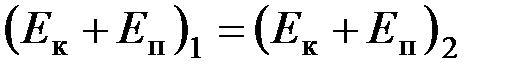где

, ;

,

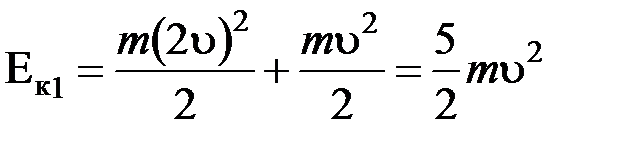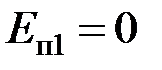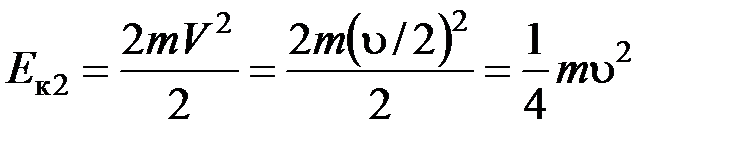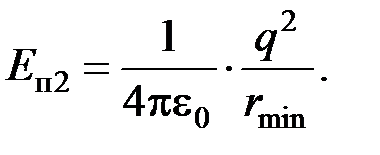
Тогда получим

,

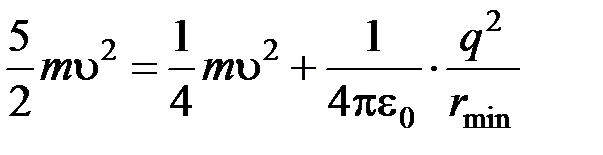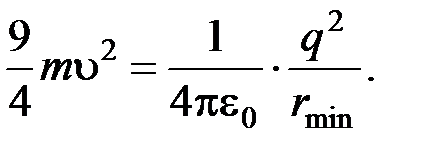
Отсюда

,

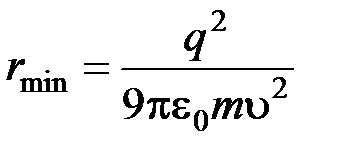где e₀ = 8,85 10 ^{– 12} Ф/м – электрическая постоянная.

Проверка размерности:

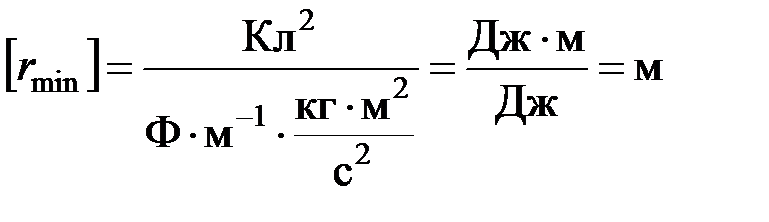
Ответ: .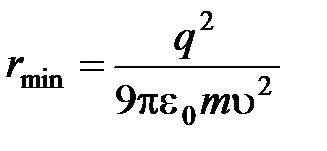

Задача № 4

Тонкий провод в виде кольца массой m = 5 г свободно подвешен на неупругой нити в однородном магнитном поле. По кольцу течет ток силой i = 6 А. Период Т малых крутильных колебаний относительно вертикальной оси равен 2,2 с. Найти индукцию В магнитного поля.

Дано: m = 5 г = 5×10 – 3 кг i = 6 А B = const T = 2,2 с

B – ?

Решение:

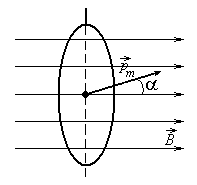
На контур с током в магнитном поле 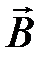действует момент силы N = B × p_m sin a, где p_m = i × S – магнитный момент кольца; S – площадь кольца.

Запишем уравнение динамики вращательного движения:

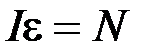, (1)

где 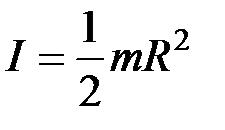– момент инерции кольца относительности оси, лежащей в плоскости кольца и проходящей через его центр; 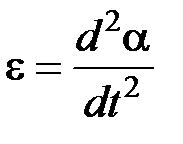– угловое ускорение (вторая производная угла поворота по времени); N – возвращающий механический момент, равный N = - B × i × S × a (при малых углах sin a » a); S = p R² – площадь кольца. Тогда уравнение (1) примет вид:

;

.

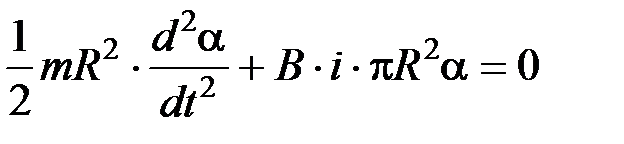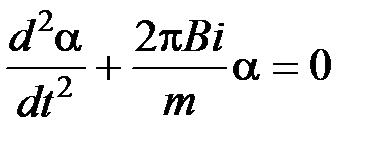Таким образом, мы получаем дифференциальное уравнение динамики гармонических колебаний, для которых циклическая частота .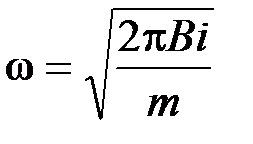

Учитывая связь периода колебаний и частоты, имеем:

.

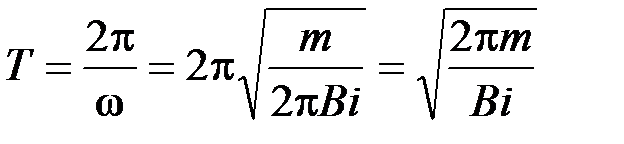Отсюда

,

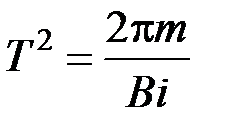следовательно,

.

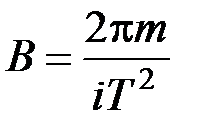Проверка размерности:

.

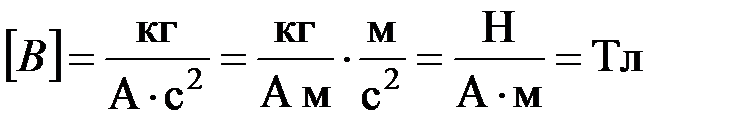Расчет:

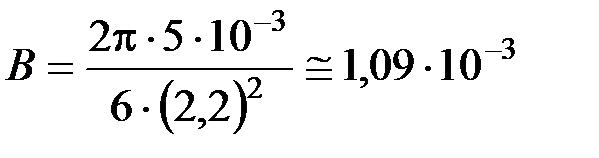(Тл).

Ответ: B = 1,09 мТл.

Задача № 5

На дифракционную решетку нормально к ее поверхности падает монохроматический свет. Постоянная дифракционной решетки в n = 4,6 раза больше длины световой волны. Найти общее число m дифракционных максимумов, которое теоретически возможно наблюдать в данном случае.

Дано: d = 4,6 l

m – ?

Решение:

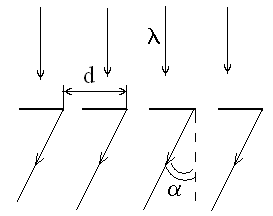
По условию максимумов для дифракционной решетки

d sin j = k l, (1)

где k = 0, 1, 2,…

Модуль sin j не может превысить единицу. Поэтому из формулы (1) вытекает, что наибольший порядок наблюдаемого максимума k_max должен быть меньше отношения периода решетки d к длине волны l, т. е.:

.

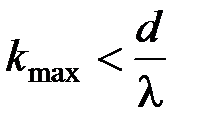Проверим размерность:

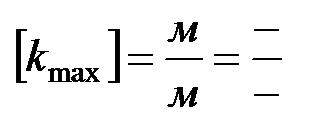
Расчет:

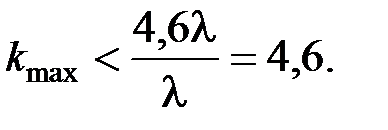
Округляем до ближайшего слева целого числа, тогда k_max = 4.

Общее количество максимумов будет равно сумме центрального максимума и числа максимумов справа и слева от центрального:

m = 4 + 4 + 1 = 9.

Ответ: 9 максимумов.

Задача № 6

Параллельный пучок электронов, ускоренный напряжением 30 В, падает нормально на экран, в котором имеется щель шириной 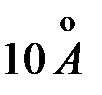. За
экраном на расстоянии 0,1 м от него параллельно щели перемещается
детектор очень малых размеров. Какова примерно ширина области, в которой детектор зарегистрирует электроны?

Дано: a = 10 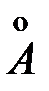= 10 – 9 м U = 30 B e = 1,6×10 – 19 Кл me = 9,1×10 – 31 кг L = 0,1 м h = 6,62×10 – 34

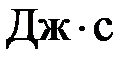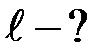Решение:

Электрическое поле, совершая работу, равную e × U, сообщает электрону кинетическую энергию E_к = e × U. Энергия покоя электрона E₀ = 0,5 МэВ. Так как E_к << E₀, для
кинетической энергии электрона можно использовать классическую формулу 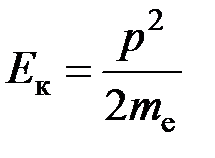, где p – импульс электрона. Отсюда:

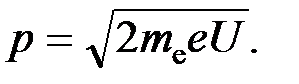
Движущийся электрон, как и любая другая микрочастица, обладает волновыми свойствами. Длина волны де Бройля для электрона имеет вид

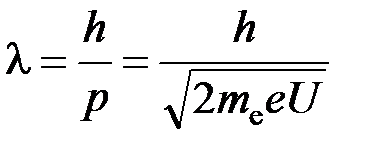, (1)

где h – постоянная Планка.

Пучок электронов испытывает дифракцию на щели. Наиболее вероятная область локализации электрона может быть отнесена к центральному максимуму дифракционной картины, граница которого определится условием минимума первого порядка:

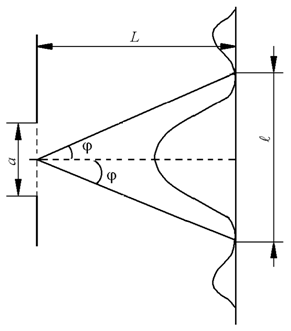a sin j = l. (2)

Подставим (1) в (2) и выразим sin j:

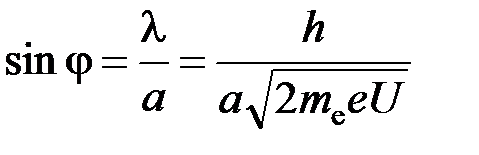. (3)

Из рисунка видно, что

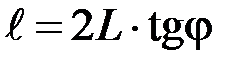. (4)

Полагая ввиду малости углов sin j @ tg j и подставляя (3) в (4), получим:

.

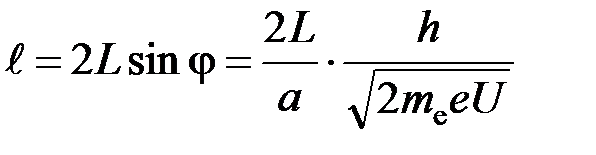Проверка размерности:

.

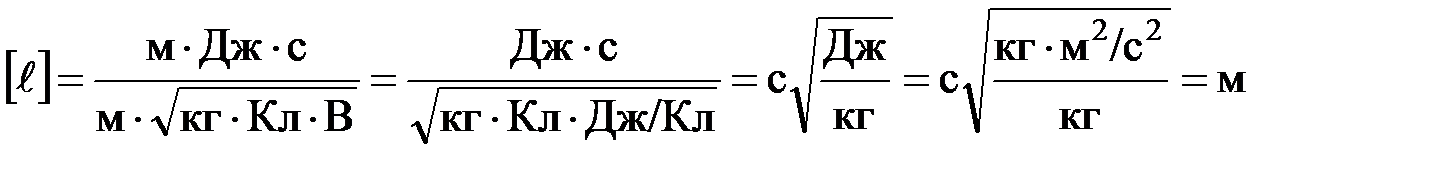Расчет:

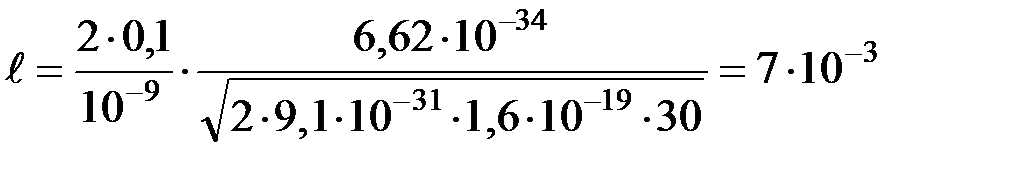(м) = 7 (мм).

Ответ: 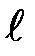= 7 мм.

Используемая литература

1. Савельев, И. В. Курс общей физики. В 3 т. Т. 1. Механика. Молекулярная физика [Текст] / И. В. Савельев. – 5-е изд., стереотип. – СПб.: Лань, 2006. – 432 с.

2. Савельев, И. В. Курс общей физики. В 3 т. Т. 2. Электричество и магнетизм. Волны. Оптика [Текст] / И. В. Савельев. – 5-е изд., стереотип. – СПб.: Лань, 2006. – 496 с.

3. Савельев, И. В. Курс общей физики. В 3 т. Т. 3. Квантовая оптика. Атомная физика. Физика твердого тела. Физика атомного ядра и элементарных частиц [Текст] / И. В. Савельев. – 4-е изд., стереотип. – СПб.: Лань, 2005. – 320 с.

4. Пиралишвили, Ш. А. Механика. Электромагнетизм. [Текст] / Ш. А. Пиралишвили, Н. А. Мочалова, З. В. Суворова, Е. В. Шалагина, В. В. Шувалов. – М.: Машиностроение, 2006. – 336 с.