Определение коэффициента поверхностного натяжения жидкости капельным методом

Выполнил студент _________________, группа____________ дата _________.

Допуск ______________

Выполнение __________

Зачет ________________

Цели работы:

3. Определить коэффициент поверхностного натяжения жидкости.

Приборы и материалы

№ п\п	Наименование прибора	Цена деления	Предел измерения (хmax)	Точность отсчета (Δхпр)
	сосуд с дистиллированной водой
	пипетка
	бюретка	-	-	-
	штатив с муфтой и лапкой
	емкость для сбора капель
	сосуд с неизвестной жидкостью

Теоретические сведения

Основные понятия и законы

Наиболее характерным свойством жидкости, отличающим ее от газа, является то, что на границе с газом жидкость образует свободную поверхность, наличие которой приводит к возникновению явлений особого рода, называемых поверхностными. Своим возникновением они обязаны особым физическим условиям, в которых находятся молекулы вблизи свободной поверхности.

На каждую молекулу жидкости действуют силы притяжения со стороны окружающих ее молекул, расположенных от нее на расстоянии порядка 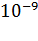м (радиус молекулярного действия). На молекулу 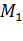, расположенную внутри жидкости (рис. 1), действуют силы со стороны таких же молекул, и равнодействующая этих сил близка к нулю.

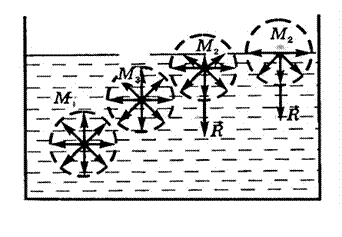Для молекул 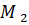равнодействующие сил отличны от нуля и направлены внутрь жидкости, перпендикулярно к ее поверхности. Таким образом, все молекулы жидкости, находящиеся в поверхностном слое, втягиваются внутрь жидкости. Но пространство внутри жидкости занято другими молекулами, поэтому поверхностный слой создает давление на жидкость (молекулярное давление).

Чтобы переместить молекулу 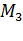, расположенную непосредственно под поверхностным слоем, на поверхность, необходимо совершить работу против сил молекулярного давления. Следовательно, молекулы поверхностного слоя жидкости обладают дополнительной потенциальной энергией по сравнению с молекулами внутри жидкости. Эту энергию называют поверхностной энергией.

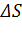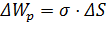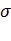Очевидно, что величина поверхностной энергии тем больше, чем больше площадь свободной поверхности. Пусть площадь свободной поверхности изменилась на , при этом поверхностная энергия изменилась на , где – коэффициент поверхностного натяжения. Отсюда,

.

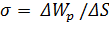Так как, для этого изменения необходимо совершить работу 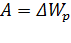, то 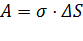. Единицей коэффициента поверхностного натяжения в СИ является джоуль на квадратный метр .

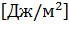Коэффициент поверхностного натяжения – величина, численно равная работе, совершенной молекулярными силами при изменении площади свободной поверхности жидкости на 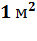при постоянной температуре.

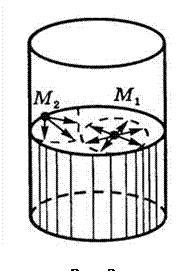Так как, любая система, предоставленная сама себе, стремится занять такое положение, в котором ее потенциальная энергия наименьшая, то жидкость обнаруживает стремление к сокращению свободной поверхности. Поверхностный слой жидкости ведет себя подобно растянутой резиновой пленке, т.е. все время стремится сократить площадь своей поверхности до минимальных размеров, возможных при данном объеме. Например, капля жидкости в состоянии невесомости имеет сферическую форму. Свойство поверхности жидкости сокращаться, можно истолковать как существование сил, стремящихся сократить эту поверхность. Молекула 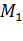(рис. 2), расположенная на поверхности жидкости, взаимодействует не только с молекулами, находящимися внутри жидкости, но и с молекулами, находящимися на поверхности жидкости, расположенными в пределах сферы молекулярного действия. Для молекулы 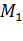равнодействующая 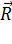молекулярных сил, направленных вдоль свободной поверхности жидкости, равна нулю, а для молекулы 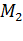, расположенной у границы поверхности жидкост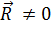и, и 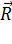направлена по нормали к границам свободной поверхности и по касательной к самой поверхности жидкости.

Равнодействующая сил, действующих на все молекулы, находящиеся на границе свободной поверхности, и есть силаповерхностного натяжения. В целом она действует так, что стремится сократить поверхность жидкости.

Можно предположить, что сила поверхностного натяжения 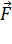прямо пропорциональна длине границы поверхностного слоя жидкости, ведь на всех участках поверхностного слоя жидкости молекулы находятся в одинаковых условиях: .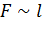

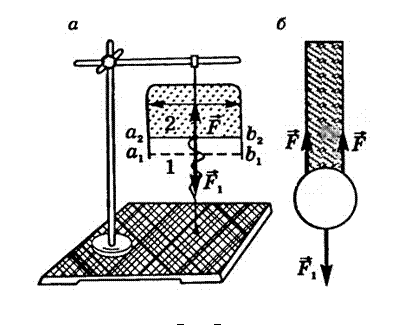Действительно, рассмотрим вертикальный прямоугольный каркас (рис. 3, а, б), подвижная сторона которого уравновешена. После извлечения рамки из раствора мыльной пленки подвижная часть перемещается из положения 1 в положение 2. Учитывая, что пленка представляет собой тонкий слой жидкости и имеет две свободные поверхности, найдем работу, совершаемую при перемещении поперечины на расстояни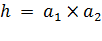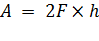е : , где 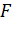– сила, действующая на каркас со стороны каждого поверхностного слоя. С другой стороны, .

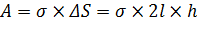Следовательно, 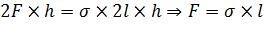, откуда

.

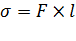Согласно этой формуле единицей коэффициента поверхностного натяжения в СИ является ньютон на метр .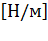

Коэффициент поверхностного натяжения 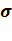численно равен силе поверхностного натяжения, действующей на единицу длины границы свободной поверхности жидкости. Коэффициент поверхностного натяжения зависит от природы жидкости, от температуры и от наличия примесей. При увеличении температуры он уменьшается.

В случае соприкосновения с твердым телом силы сцепления молекул жидкости с молекулами твердого тела начинают играть существенную роль. Поведение жидкости будет зависеть от того, что больше: сцепление между молекулами жидкости или сцепление молекул жидкости с молекулами твердого тела.

Смачивание – явление, возникающее вследствие взаимодействия молекул жидкости с молекулами твердых тел. Если силы притяжения между молекулами жидкости и твердого тела больше сил притяжения между молекулами жидкости, то жидкость называют смачивающей; если силы притяжения жидкости и твердого тела меньше сил притяжения между молекулами жидкости, то жидкость называют несмачивающей это тело.

Одна и та же жидкость может быть смачивающей и несмачивающей по отношению к разным телам. Так, вода смачивает стекло и не смачивает жирную поверхность, ртуть не смачивает стекло, а смачивает медь.

Смачивание или несмачивание жидкостью стенок сосуда, в котором она находится, влияет на форму свободной поверхности жидкости в сосуде. Если большое количество жидкости налито в сосуд, то форма ее поверхности определяется силой тяжести, которая обеспечивает плоскую и горизонтальную поверхность. Однако у самых стенок явление смачивания и несмачивания приводят к искривлению поверхности жидкости, так называемые краевые эффекты.

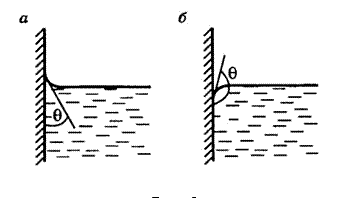
Количественной характеристикой краевых эффектов служит краевой угол 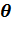– угол между плоскостью касательной к поверхности жидкости и поверхностью твердого тела. Внутри краевого угла всегда находится жидкость (рис. 4, а, б). При смачивании он будет острым (рис. 4, а), а при несмачивании – тупым (рис. 4, б). В школьном курсе физики рассматривают только полное смачивание 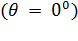или полное несмачивание .

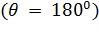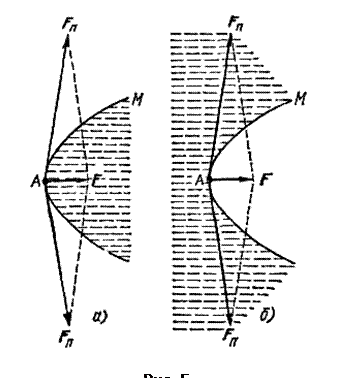
Силы, связанные с наличием поверхностного натяжения и направленные по касательной к поверхности жидкости, в случае выпуклой поверхности дают результирующую, направленную внутрь жидкости (рис. 5, а). В случае вогнутой поверхности результирующая сила направлена, наоборот, в сторону газа, граничащего с жидкостью (рис. 5, б).

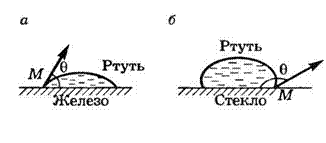
Если смачивающая жидкость находится на открытой поверхности твердого тела (рис. 6, а), то происходит ее растекание по этой поверхности. Если на открытой поверхности твердого тела находится несмачивающая жидкость, то она принимает форму, близкую к шаровой (рис. 6, б).

Смачивание имеет важное значение как в быту, так и в промышленности. Хорошее смачивание необходимо при крашении, стирке, обработке фотоматериалов, нанесении лакокрасочных покрытий, при склеивании материалов, при пайке, во флотационных процессах (обогащение руд ценной породой). И, наоборот, при сооружении гидроизоляционных устройств необходимы материалы, не смачиваемые водой.

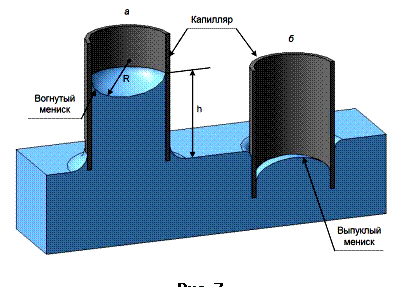
Искривление поверхности жидкости у краев сосуда особенно отчетливо видно в узких трубках, где искривляется вся свободная поверхность жидкости. В трубках с узким сечением эта поверхность представляет собой часть сферы, ее называют мениском. У смачивающей жидкости образуется вогнутый мениск (рис. 7, а), а у несмачивающей – выпуклый (рис. 7, б). Так как площадь поверхности мениска больше, чем площадь поперечного сечения трубки, то под действием молекулярных сил искривленная поверхность жидкости стремится выпрямиться.

Силы поверхностного натяжения создают дополнительное (лапласово)давление под искривленной поверхностью жидкости. Искривление поверхностного слоя приводит к появлению дополнительного давления на жидкость 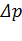, зависящего от поверхностного натяжения 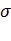и кривизны поверхности:

,

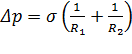где 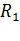и 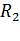– радиусы кривизны двух взаимоперпендикулярных сечений поверхности (если поверхность сферическая, то 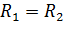). . 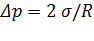Для цилиндрической поверхности 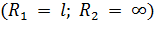избыточное давление .

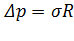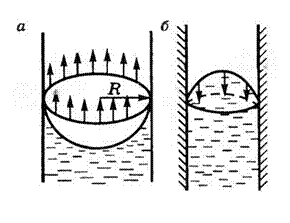
Если поверхность жидкости вогнутая, то сила поверхностного натяжения направлена из жидкости (рис. 8, а), и давление под вогнутой поверхностью жидкости меньше, чем под плоской, на 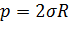. Если поверхность жидкости выпуклая, то сила поверхностного натяжения направлена внутрь жидкости (рис. 8, б), и давление под выпуклой поверхностью жидкости больше, чем под плоской, на ту же величину.

Если поместить узкую трубку (капилляр) одним концом в жидкость, налитую в широкий сосуд, то вследствие наличия силы лапласова давления жидкость в капилляре поднимается (если жидкость смачивающая) или опускается (если жидкость несмачивающая) (рис. 9), так как под плоской поверхностью жидкости в широком сосуде избыточного давления нет.

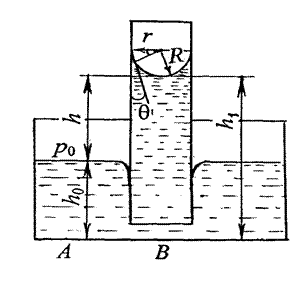Явления изменения высоты уровня жидкости в капиллярах по сравнению с уровнем жидкости в широких сосудах называютсякапиллярными явлениями. Жидкость в капилляре поднимается или опускается на такую высоту 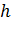, при которой сила гидростатического давления столба жидкости уравновешивается силой избыточного давления, т.е. 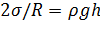. Откуда:

.

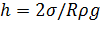Если смачивание не полное 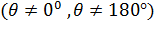, то радиусы капилляра и мениска не равны и связаны соотношением 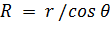, тогда: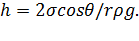

Теория лабораторной работы

Коэффициент поверхностного натяжения жидкости определяется методом капель. Исследуемая жидкость налита в стеклянную трубку, заканчивающуюся капилляром малого радиуса 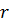, из которого вытекает жидкость в виде капель.

Рассмотрим процесс образования капель. Вытеканию жидкости из капилляра препятствует поверхностная пленка, состоящая из молекул жидкости. Под воздействием силы тяжести пленка прогибается, растягивается, увеличивается, стремясь приобрести сферическую форму . В некоторый момент у капли появляется перетяжка («шейка»), радиус которой можно приблизительно считать равным радиусу капилляра 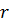(рис 9).

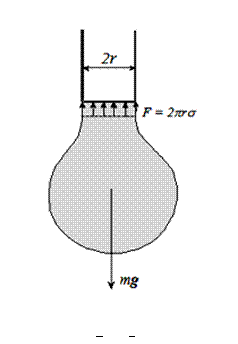По окружности этой перетяжки действуют силы поверхностного натяжения, препятствующие отрыву капли. Силу поверхностного натяжения 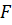при отрыве капли можно подсчитать, зная радиус шейки :

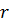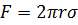(1)

В момент отрыва капли ее вес 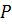равен силе поверхностного натяжения 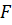, т.е.

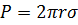(2)

Отсюда легко получить

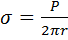. (3)

На практике вес одной капли определяют через объём нескольких капель и плотность жидкости.

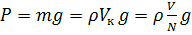, (4)

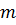где и 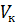– масса и объем одной капли исследуемой жидкости, 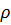– плотность исследуемой жидкости; 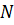– количество капель исследуемой жидкости, содержащихся в объеме 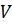. Тогда:

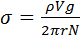(5)

Измерения и обработка результатов:

1. Налейте в бюретку исследуемую жидкость (1 – дистиллированная вода, 2 – технический спирт);

2. Отрегулируйте с помощью крана скорость истечения жидкости: число капель, отрывающихся в минуту, должно быть порядка .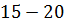

3. Определите 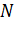– количество капель воды, занимающих некоторый объем 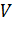между соседними метками на трубке. Для этого, когда уровень воды сравняется с одной из верхних меток, начните считать капли. Счет прекратите, когда уровень жидкости сравняется с соседней нижней меткой.

4. Повторите эксперимент не менее 3 раз, изменяя объём вытекающей жидкости (измениться число капель ).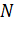

5. Занесите данные в таблицу и предъявите преподавателю.

№ опыта	Темпера- тура жидкости 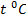.	Радиус капилляра 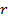.	Число капель	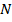Обьём капель	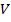Плотность жидкости	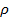Коэфициент поверхностного натяжения	Доверитель-ный интервал

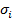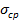Контрольные вопросы

17. Опишите механизм возникновения поверхностного натяжения жидкостей.

18. Дайте определение коэффициента поверхностного натяжения. Каков его физический смысл?

19. Чем обусловлено поверхностное натяжение жидкостей?

20. Выведите выражение для работы, которую нужно совершить, чтобы изменить площадь поверхности жидкости.

21. От чего зависит коэффициент поверхностного натяжения?

22. В чем заключаются явления смачивания и несмачивания?

23. Опишите причины капиллярных явлений.

24. Выведите рабочие формулы для определения коэффициента поверхностного натяжения жидкости для метода капель.

25. Дайте описание установки для измерений и порядок проведения эксперимента.

ЛИТЕРАТУРА

6. Физический практикум: Механика и молекулярная физика / под ред. проф. В.И. Ивероновой. – М.: Наука, 1967.

7. Сивухин Д.В. Общий курс физики. Т.2. Термодинамика и молекулярная физика. – М: Физматлит, 2005-544.

8. Савельев И.В. Курс общей физики. Т.3. Термодинамика и молекулярная физика. – Спб; M; Краснодар: Лань. 2005.

9. Трофимова Т.И. Курс физики. М.: Высш. Школа, 2005.

10. Яворский Б.М., Детлаф А.А. Справочник по физике. М.: Наука, 1985.

[1] О классе точности приборов см.: Указания к выполнению лабораторных работ, ч. 2 «Электричество и магнетизм».

[2] ГОСТ 8.207-76 устанавливает, что если Dx_сист < 0,8, то следует пренебречь систематической составляющей погрешности и учитывать только случайную погрешность результата в виде . Если Dx_сист > 0,8, то, наоборот, следует пренебречь случайной составляющей и результат измерений характеризовать его систематической погрешностью

[3] Строго говоря, погрешность результата измерения Δх следует выражать одной или двумя значащими цифрами. Две цифры оставляют при наиболее точных измерениях, а также в тех случаях, когда цифра старшего разряда числа, выражающего погрешность, меньше или равна 3.

1 e - греч. «эпсилон»

[4] Аксиальные векторы не связаны с определенной линией действия. Их можно перемещать в пространстве параллельно самим себе (свободные векторы).

1 За одно полное колебание тело проходит расстояние S =4A.

2 Момент инерции - скалярная величина, характеризующая распределения масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении.

Момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния а между осями: J = J_c + ma².

1 Аксиальные векторы не связаны с определенной линией действия. Их можно перемещать в пространстве параллельно самим себе (свободные векторы).

2 См. лабораторную работу № 12.

1 Период простого колебания равен половине периода полного колебания.

1 Аксиальные векторы не связаны с определенной линией действия. Их можно перемещать в пространстве параллельно самим себе (свободные векторы).

[6] Градиент - мера возрастания или убывания в пространстве какой-л. физической величины при перемещении на единицу длины. Многие физические величины могут не только изменяться с течением времени, но и быть различными в разных точках пространства в один и тот же момент времени. Под «скоростью» понимают темп изменения физической величины во времени, а под «градиентом» — степень её изменения в пространстве.

1 Гомогенный - однородный по своему составу или происхождению.

2 Гетерогенный - состоящий из различных по составу, свойствам, происхождению частей.

1 Градиент – мера возрастания или убывания в пространстве какой-либо физической величины на единицу длины.

2 Триботехника – наука о контактном взаимодействии твердых тел при их относительном движении.

1 Другое определение: фаза — гомогенная часть гетерогенной системы.

1 Необходимо обратить внимание на слова “единственным результатом»; запреты второго начала снимаются, если процессы, о которых идет речь, не является единственными.

2 то есть каждому состоянию соответствует определённое значение энтропии.

3 Знаком dQ обозначено то, что количество теплоты не является полным дифференциалом, так как зависит не только от начального и конечного состояния системы, но и от пути перехода.

4 Флуктуация – случайное отклонение величины, характеризующей систему из большого числа частиц, от её среднего значения.