Вращение плоскости поляризации

Оптическая активность. Естественную оптическую активность вещества можно наблюдать с помощью следующей установки. Параллельный пучок света направляется на систему, изображённую на рис.5.1.

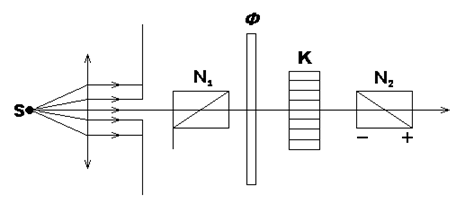Рис. 5.1 Наблюдение оптической активности вещества

Между скрещёнными николями N₁ и N₂ расположены светофильтр Ф (для монохроматизации света) и пластинка из кристаллического кварца K, оптическая ось которой совпадает с направлением луча. Так как вдоль оптической оси не происходит двойного лучепреломления, то при скрещённом положении николей свет не должен проходить через систему. Однако, как показал опыт, наблюдается прохождение света через систему. Это может произойти только в том случае, если пластинка кварца поворачивает плоскость поляризации на некоторый угол. Если это так, то вращением николя N₂ вокруг оси луча на тот же угол в противоположном направлении можно скомпенсировать поворот плоскости поляризации и добиться тем самым полного затемнения поля на экране. Описанный опыт полностью подтверждает это предположение.

Явление вращения плоскости поляризации впервые было обнаружено Араго в 1811 г. при изучении двойного лучепреломления в кварце. Вещества, способные вращать плоскость поляризации в отсутствие внешних воздействий, называются оптически активными. Оптическая активность, существующая в отсутствие какого-либо внешнего воздействия, называется естественной. Существует множество кристаллов и аморфных тел, обладающих оптической активностью. В качестве примера оптически активных веществ можно привести скипидар, камфару, никотин, раствор сахара, киноварь, биологические макромолекулы.

Принято определять направление вращения плоскости поляризации относительно наблюдателя, смотрящего навстречу падающему лучу. Вращение называется правым (положительным), если плоскость поляризации поворачивается вправо (по часовой стрелке) для наблюдателя, и левым (отрицательным), если она поворачивается влево (против часовой стрелки).

На основе экспериментальных данных было установлено, что существуют две модификации кварца, одна из которых является правовращающей, а другая – левовращающей. Значение угла вращения в обоих случаях одинаково по абсолютной величине.

Опыты, проведённые с помощью установки, изображённой на рис. 5.1, при разных светофильтрах (разных длинах волн) и прочих равных условиях показали, что величина угла вращения плоскости поляризации зависит от длины волны, т. е. имеет место дисперсия вращательной способности.

Определение угла вращения. Опыты с пластинками кварца разной толщины показали, что для данной длины волны величина угла поворота плоскости поляризации прямо пропорциональна длине пути луча в оптически активной среде, т.е.

j = al, (5.1)

где j – угол поворота плоскости поляризации;

l – толщина пластинки;

a – постоянная вращения, показывающая чему равен угол поворота при толщине пластинки 1 мм.

Коэффициент a зависит от рода вещества, температуры и от длины волны прошедшего через него света.

В результате экспериментальных исследований, проведенных Био в 1831 г. с жидкими оптически активными растворами, была установлена зависимость угла поворота от концентрации

j = [a] Сl , (5.2)

где C – концентрация растворённого вещества, кг/м³;

[a] – удельное вращение, численно равное углу поворота плоскости поляризации при прохождении в растворе 1 метра при концентрации, равной 1 кг/м³.

Величина [a] зависит, как и a, от длины волны используемого монохроматического света, а так же от температуры.

Био установил также следующую приближённую зависимость постоянной вращения a и удельным вращением [a] от длины волны l

a ~1/l² и [a] ~1/l² . (5.3)

Позже Друде установил, что

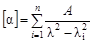, (5.4)

где A – постоянная величина;

λ_i – длина волн, соответствующих собственным колебаниям системы.

Гипотеза Френеля. Объяснение вращения плоскости поляризации впервые было дано Френелем (1817г.). Согласно гипотезе Френеля, вращение плоскости поляризации обусловлено особым типом лучепреломления, при котором волны, поляризованные вправо и влево по кругу, распространяются с разной скоростью в оптически активном веществе. Знак угла вращения плоскости поляризации определяется соотношением скоростей циркулярно поляризованных волн V_л (для левокруговой волны) и V_пр (для правокруговой волны). При V_пр > V_л отически активное вещество, по Френелю, называется правовращающим (или просто “правым”) если же V_пр < V_л, то левовращающим (или просто “левым”).

Можно показать, что гипотеза Френеля формально объясняет явление вращения плоскости поляризации. Линейно-поляризованную волну (E), как известно, можно разложить на две волны, поляризованные по правому (E_пр) и по левому (E_л) кругам (рис 5.2). При V_пр = V_л число оборотов электрических векторовE_пр и E_л в слое вещества толщиной l, будет одинаковым и результирующее (исходное) колебание будет происходить вдоль E, т.е. среда не обладает свойством оптической активности.

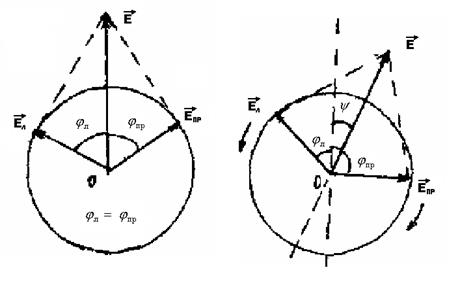
Рис 5.2. Объяснение вращения Рис. 5.3 Вычисление угла

плоскости поляризации поворота плоскости поляризации

Если же V_пр ≠ V_л, то число оборотов векторов E_пр и E_л различно и в итоге они повернутся на различные углы j_пр и j_л, что приведёт к повороту результирующего вектора E на некоторый угол ψ. Исходя из предположения, что V_пр > V_л, можно вычислить угол ψ (рис.5.3). После прохождения циркулярно-поляризованными волнами оптически активной среды толщиной l электрический вектор правой волны повернется вправо на бόльший угол, чем вектор левой волны, так как правая волна распространяется с большей скоростью. В итоге плоскость симметрии, разделяющая пополам сумму углов j_пр и j_л, будет повёрнута вправо на угол ψ, определяемый из условия j_пр -y = j_л + y . Отсюда

y = (j_пр - j_л)/2 , (5.5)

Выразив j_пр и j_л через время t и длину пути волн в оптически активной среде l

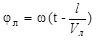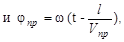получим окончательное выражение для ψ

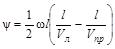. (5.6)

Если фазовые скорости распространения левой и правой волн V_л и V_пр выразить через соответствующие коэффициенты преломления n_л и n_пр (V_пр = с/n_пр и V_л = с/n_л) и принять во внимание что, 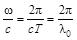, где λ₀ - длина волны в вакууме, то получим

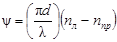. (5.7)

Как следует из формулы (5.7), при п_л > п_пр ( V_л < V_пр) ψ является положительным, т.е. вращение плоскости поляризации происходит вправо, а при п_л < п_пр ( V_л >V_пр) ψ становится отрицательным, т.е. вращение происходит влево.

Описание поляриметров

Поляриметры применяются в научно-исследовательской работе, в ряде отраслей промышленности (химической, пищевой и др.) и в медицине для определения степени оптической активности вещества и связанных с нею физико-химических свойств этого вещества.

На рис. 5.4 приведена схема кругового поляриметра. Измерительной частью кругового поляриметра является головка анализатора, состоящая из неподвижного лимба 1, диска 2 с двумя нониусами и анализатора 3 -они вращаются совместно, а также зрительной трубки 4, служащей для рассматривания поля зрения, разделенного на три части. Перемещением муфты 5 производится установка окуляра на резкое изображение границы и линий раздела поля зрения. С помощью той же муфты можно поворачивать анализатор и диск с нониусами.

В головку поляризатора 8, повернутую в сторону источника света 12, входят поляризатор 9, кварцевая пластинка 10 и конденсор 11. Обе головки соединены трубкой 6 с длинной прорезью, которая закрывается вращающейся вокруг продольной оси ширмой; в соединительную трубку вкладывается кювета в виде узкой трубки, заполняемая водным раствором сахара.

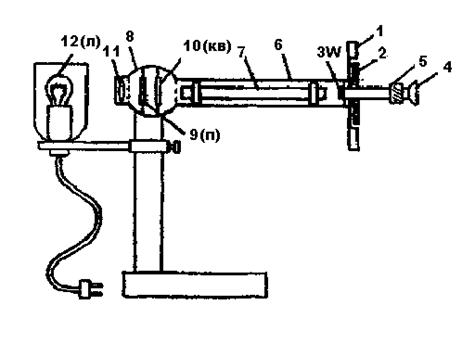
Рис. 5.4. Круговой поляриметр

В поляриметрах указанных выше разновидностей используется принцип уравнивания освещенности разделенного на три (или две) части поля зрения. Его разделение осуществляется в круговом поляриметре благодаря введению в оптическую систему кварцевой пластинки, которая занимает среднюю часть поля зрения. Пластинка эта может быть вырезана перпендикулярно оптической оси кристалла кварца, тогда в ней не будет происходить двойного лучепреломления, а будет иметь место вращение плоскости поляризации (кварц - оптически активное вещество). Толщина пластинки берется такой, чтобы плоскость поляризации входящего в нее света поворачивалась на 5-7°. Уравнивание освещенности частей поля зрения нужно проводить вблизи полного затемнения крайних и средней частей поля зрения, т.е. вблизи положения скрещивания поляризатора и анализатора (j= 86-87°), -такое положение анализатора называется чувствительным. Уравнивания освещенности частей поля зрения (фотометрического равновесия) можно достигать и при почти параллельном положении плоскостей пропускания поляризатора и анализатора (j = 3-4°),но при этом точность измерений уменьшается примерно на порядок.

Свет от лампы накаливания, пройдя через конденсор 11 и поляризатор 9, затем средней частью выделенного пучка проходит через кварцевую пластинку 10, защитное стекло (оно является также светофильтром) и анализатор 3. Крайние части пучка проходят только через защитное стекло и анализатор (см. рис.5.4; рисунок выполнен при условии, что кювета с раствором сахара в приборе отсутствует).

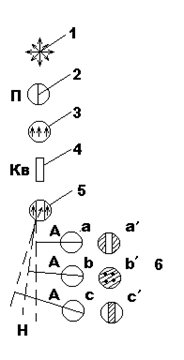
1. Естественный свет

2. Плоскость пропускания поляризатора

3. Положение векторов Е в пучке света, вышедшем из поляризатора.

4. Кварцевая пластинка

5. Положение векторов Е в свете после кварцевой пластинки

6. Положения плоскостей пропускания анализатора (a, b, c) и соответствующие им поля зрения (а', b', с').

Рис. 5.5. Объяснение возникновения тройного (или двойного)

поля зрения в поляриметре

Если плоскость пропускания анализатора перпендикулярна плоскости пропускания поляризатора, то крайние части поля зрения максимально затемнены, а средняя является светлой. Если же плоскость пропускания анализатора перпендикулярна направлению вектора Ев средней части пучка, в которой свет проходит через кварцевую пластинку, то темной является средняя часть поля зрения. Но если плоскость пропускания анализатора перпендикулярна к биссектрисе угла между направлениями вектора Е в средней и в крайних частях светового пучка (F, H), то все части поля зрения будут иметь одинаковую (малую) яркость, и границы между ними почти не будут видны. Вводя между анализатором и поляризатором кювету с оптически активным раствором сахара, мы нарушаем фотометрическое равновесие. Восстановить его можно, повернув анализатор на угол, равный углу поворота плоскости поляризации света раствором сахара, Определив угол между начальным ("нулевым") и новым положения анализатора, мы можем узнать угол поворота поляризации оптически активным веществом. На лимбе I (рис. 5.4) нанесена по часовой стрелке градусная шкала от 0° до 360°. Внутри лимба на подвижном диске, связанном с анализатором, нанесены два нониуса, расположенные диаметрально противоположно; нониусы имеют по двадцать делений и позволяют измерять углы с точностью 0,05. Если нуль нониуса не совпадает с каким-либо штрихом на шкале лимба, то, заметив какой штрих нониуса совпадает с градусным штрихом лимба, можно определить, сколько десятых и сотых долей градуса надо прибавить к целому числу градусов, показываемых нулевым штрихом нониуса. Например, нулевой штрих нониуса находится между 33°и 34°,а совпадает с некоторым штрихом лимба девятый штрих нониуса (первый после штриха с цифрой 4). Тогда "нулевое" положение анализатора будет таким: 33° + 9 • 0,05° = 33,45°.

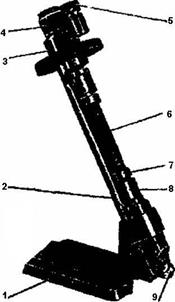
Рис.5.6. Портативный поляриметр

1.Кронштейн

2.Соединительная трубка

3.Головка анализатора

4.Оправа

5.Отсчётная лупа

6.Трубка для растворов

7.Втулка

8.Раковина

9.Зеркало

На рис. 5.6 приведен портативный поляриметр. Головка анализатора 3 портативного поляриметра состоит из зрительной трубки, неподвижного лимба с градусной шкалой и совместно вращающихся анализатора, нониуса и отсчётной лупы 5. Головка анализатора связана с поляризационным устройством соединительной трубкой 2, в широкий разрез которой вставляется трубка с раствором 6.

На соединительной трубке внизу крепится зеркало в оправе. Как анализатор, так и поляризатор представляют собой поляроидные пленки, заключенные между двумя защитными стеклами. В поляризационное устройство входят также оранжевый светофильтр и кварцевая пластинка, имеющая вид полукруга; она занимает половину поля зрения. Кварцевая пластинка поворачивает плоскость поляризации вступающего в неё света на 4-5° и тем самым делит поле зрение на две различно освещенные части. На неподвижном лимбе вправо и влево от нуля нанесены 20 делений; цена деления лимба 1°. В плоскости лимба на подвижной втулке имеются два нониуса - левый и правый; каждый нониус разделен на 10 делений. Максимальное значение величины отсчёта по нониусу – 0,1^о .

Порядок выполнение работы

1. Включить в сеть осветитель. Перемещением осветителя или прибора добиться равномерного освещения поля зрения (его частей) при удалённой из кюветного отделения трубки с раствором. Перемещением муфты (или оправы окуляра) установить окуляр на резкое изображение границы поля зрения. После этого вращением той же муфты (или кольца) повернуть анализатор до установления фотометрического равновесия в чувствительном положении (т.е. при минимальной общей освещенности поля зрения).

1. Установку прибора на фотометрическое равновесие произвести не менее 5 раз. Отсчеты по лимбу и нониусу занести в таблицу. Средняя величина j₀ и является нулевым отсчетом прибора. Если нулевой штрих нониуса при достижении фотометрического равновесия оказывается при использовании портативного поляриметра смещенным относительно нулевого штриха лимба по часовой стрелке, то нулевому отсчету приписывается знак "плюс", если же против часовой стрелки, то знак "минус". Знак нулевого отсчета затем учитывается при определении угла поворота плоскости поляризации.

3. Определить среднее значение нулевого отсчета и среднее
значение абсолютной погрешности.

4. Поместить трубку с раствором сахара в кюветное отделение
соединительной трубки, закрыть шторку (при использовании кругового поляриметра). При этом происходит нарушение фотометрического равновесия. Установить окуляр по глазу на резкое изображение границ.

5. Поворотом анализатора восстановить фотометрическое равновесие. Пять раз произвести отсчет угла j'; рассчитать его среднее значение, а затем абсолютные погрешности и их среднее значение.

6. Определить угол поворота плоскости поляризации:

j=`j¢-`j ₀

7. Оценить абсолютную погрешность определения этого угла:

Dj=`Dj¢ +`Dj ₀

1. Вычислить концентрацию С сахара в растворе по формуле закона Био

j= [a]Сl

9. Рассчитать относительную и абсолютную погрешности определения концентрации сахара в растворе:

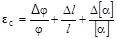и DС = e_С`С

Для сахара [a] =0,665 град×м²/кг при 293 К; D[a] = 0,001 град×м²/кг; длина трубки с раствором в круговом поляриметре 200 мм, в портативном поляриметре - 95 мм; Δl = 1 мм.

Таблица

№	Знак поправки	Число делений лимба/ нониуса	φ0	Δφ0	φ/	Δφ/	φ	Δφ	ε0	`С	ΔC

Средние значения	j0	Δj0	j/	Δj/

Окончательный результат: C =`C ± DC =

Вопросы для допуска к работе

1. Цель работы.

2. Что выражает формула j = [α]Cl? Каков физический смысл
удельного вращения [α]?

3. Как можно определить абсолютную и относительную
погрешности измерения концентрации сахара с помощью
поляриметра?

4. Что такое фотометрическое равновесие и как оно достигается?

Контрольные вопросы

1. Чем отличаются друг от друга естественный и плоско -
поляризованный свет?

2. Что такое оптическая активность вещества? Сформулируйте законы
Био для явления вращения плоскости поляризации.

3. Сформулируйте и запишите закон Малюса. Для объяснения каких
фактов этот закон используется в работе?

4. Перечислите основные части поляриметра, укажите их назначение.

5. Каково назначение кварцевой пластинки в поляриметре? Объясните,
как надо установить анализатор для получения фотометрического
равновесия.

Литература

1. Савельев И.В. Курс общей физики. Т. 2.- М.: Наука, 1972. гл. 19, §134, 141.

2. Ландсберг Г. С. Оптика. - М.: Наука, 1976. Гл. 16, §101, 104, 105; гл. 30, §168, 169.

3. Сивухин Д.В. Общий курс физики. Оптика. Т.4. - М.: Наука, 1980. гл. 8, §94.

4. Детлаф А.А., Яворский Б.М. Курс физики.- М.: Высш. шк., 2002. Гл. 34.

5. Гаджаев Н. М. Оптика. - М.: Высш. шк., 1977 г., гл. 12, §§5, 6.

Лабораторная работа № 6

Экспериментальная проверка закона Стефана- Больцмана

Цель работы: ознакомление с законами теплового излучения; экспериментальное определение показателя степени температуры в формуле закона Стефана- Больцмана.

Приборы и принадлежности: электрическая лампа на 220 В, трансформатор, вольтметр на 250 В, амперметр 0,5 или 1А, провода.

Краткая теория

Тепловым (температурным) излучением называется электромагнитное излучение, которое возникает при возбуждении атомов и молекул вследствие их участия в тепловом движении. Из этого определения следует, что все тела являются источниками теплового излучения. Раcкалённые (и вообще нагретые) твердые и жидкие тела дают сплошной спектр излучения; в этом спектре присутствуют волны всех длин. Доля энергии, приходящейся на различные участки спектра, зависит от температуры излучающего тела: от температуры зависит и общее количество испускаемой телом энергии. Так, при температуре 600-700°С наибольшая энергия излучения приходится на инфракрасную и красную части спектра (красное каление). При дальнейшем нагревании тела доля энергии, приходящейся на видимые лучи, возрастает, и свечение тела становиться сначала оранжево- жёлтым, а затем и белым (белое каление). В общем, в спектре излучения имеет место неравномерное распределение энергии по длинам волн.

Если на тело падает поток энергии, то часть этого потока поглощается телом. В состоянии теплового равновесия температура тела не меняется, поскольку энергия, поглощаемая телом, теряется им путём излучения.

Интенсивность теплового излучения и его спектральный состав зависят от температуры, химической природы тела, агрегатного состояния его вещества.

Спектральными характеристиками теплового излучения являются: спектральная плотность энергетической светимости (иначе: монохроматическая излучательная способность) и спектральный коэффициент поглощения (монохроматическая поглощательная способность).

Спектральной плотностью энергетической светимости называется величина, измеряемая энергией электромагнитного излучения, испускаемого за единицу времени с единичной площади поверхности излучающего тела в единичном интервале длин волн (при данной температуре):

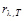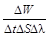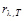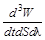= , или = (6.1)

Энергетической светимостью (интегральной излучательной способностью) тела называется величина, численно равная энергии излучения всех длин волн с единицы поверхности тела за единицу времени (также при данной определённой температуре):

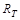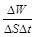= , или 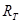= 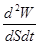. (6.2)

Интегральная излучательная способность связана с монохроматической следующим образом:

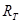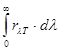= (6.3)

Спектральный коэффициент поглощения а_l,Т выражается отношением поглощенной телом энергии dW к полной энергии dW_l падающего на него излучения в интервале длин волн от l до l+dl при температуре Т:

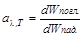. (6.4)

Функции r_l,T и a_l,T специфичны для каждого тела, они зависят не только от λ и Т, но и от химического состава, формы и состояния поверхности тела. Для всех тел a_l,T < 1. Как показывает теория теплового излучения, наиболее простой вид функция a_l,T имела бы для тела, спектральный коэффициент поглощения которого был бы равен единице для всех длин волн и при любых температурах. Теоретическая модель тела, которое поглощает всю падающую на него энергию при температуре в диапазоне длин волн от 0 до 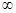, называется абсолютно чёрным телом. Модель абсолютно чёрного тела можно реализовать, если изготовить зачерненный изнутри ящик (полый цилиндр или полый шар) с узким отверстием (рис. 6.1).

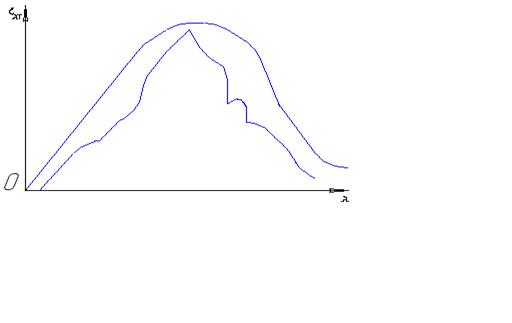
Согласно закону Кирхгофа, излучательная способность абсолютно чёрного тела r_l,T ( её обычно обозначают e_T ) в любом интервале длин волн и в любом участке спектра больше, чем излучательная способность любого тела, взятого при температуре абсолютно чёрного тела Т. На рис. 6.2 представлены графики распределения энергии абсолютно чёрного тела (рассчитанного по формуле Планка ) и нечёрного тела с a_l,T < 1.

Рис. 6.1 Модель абсолютно чёрного тела.

el,T rl,T

Рис.6.2. Распределение энергии в спектре абсолютного черного и нечерного (серого) тел

Одним из основных законов излучения абсолютно чёрного тела является закон Стефана- Больцмана: энергетическая светимость абсолютно чёрного тела пропорциональна четвертой степени его абсолютной температуры:

R_э = sТ⁴ , (6.5)

где σ =5,673·10^-8 Вт/(м²×К⁴)-постоянная Стефана- Больцмана.

Интегральную излучательную способность (энергетическую светимость) нечёрного тела можно выразить формулой:

R_э = asТ⁴ . (6.6)

Здесь a<1- коэффициент излучения тела (коэффициент черноты или степень черноты тела).

В данной лабораторной работе используется обычная лампа накаливания с вольфрамовой нитью. Мощность излучения лампы получим, умножая интегральную излучательную способность на площадь нити накаливания:

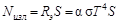. (6.7)

Полагая (с достаточной степенью точности ), что вся подводимая к лампе мощность электрического тока расходуется на излучение лампы, т.е. N_{эл.тока}=N_изл , можно записать

N = asT⁴S . (6.8)

Прологарифмировав обе части выражения (6.8), получаем:

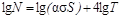. (6.9)

Если закон Стефана- Больцмана строго соблюдается и a не зависит от Т, то lgN линейно зависит от lgТ, причем тангенс угла наклона прямой на графике

lgN= f(lgТ) равен показателю степени в формуле:

R_э = sT ⁿ . (6.10)

При неизвестной величине показателя степени температуры выражение (6.9) примет вид:

LgN =lg(asS) + nlgT . (6.11)

Для определения величины n необходимо в логарифмической системе координат построить график зависимости мощности N от температуры Т для всех значений N и T , получаемых в опытах. График зависимости N = f(T) в логарифмической системе координат удобно построить в EXCEL, используя ПК. Величину показателя n можно определить по уравнению линии тренда, c указанием величины достоверности R аппроксимации опытных данных. При построении графика опытные точки обозначить маркерами без линий.

При отсутствии компьютера график зависимости можно построить на миллиметровой бумаге, предварительно определив lnN и lnT или lgN и lgT . При построении графика масштабные коэффициенты по осям желательно брать одинаковые (например, 1Î10 мм). В этом случае показатель n равен тангенсу угла наклона аппроксимирующей прямой к оси абсцисс.

Описание установки

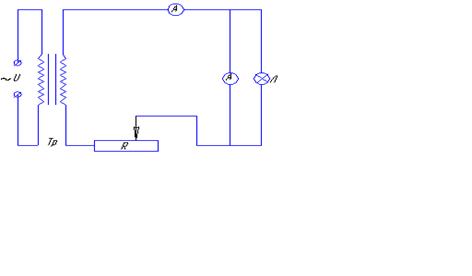
Лампа Л включена в сеть переменного тока через трансформатор Тр (рис. 6.3).

Рис. 6.3. Схема установки

Амперметр и вольтметр позволяют определить электрическую мощность N, потребляемую лампой Л, и её сопротивление R по формулам:

N=IU. (6.12)

R=U/I. (6.13)

Температуру нити накала можно вычислить, используя формулу зависимости сопротивления от температуры:

R = R₀(1 + a_R t^o) ;

из нее получаем:

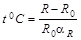, (6.14)

где R₀ – сопротивление нити накала при 0°С;

α_R – температурный коэффициент сопротивления вольфрама, в рабочем интервале температур α_R=6·10^-3 град^-1.