Поверхностное натяжение жидкости. Давление Лапласа.

Поверхность жидкости, соприкасающаяся с другой средой, находится в особых условиях по сравнению с остальной массой жидкости. Силы, действующие на каждую молекулу поверхностного слоя жидкости, граничащей с паром, направлены в сторону объёма жидкости, то есть внутрь жидкости. Вследствие этого для перемещения молекулы из глубины жидкости на поверхность требуется совершить работу. Если при постоянной температуре увеличить площадь поверхности на бесконечно малую величину dS , то необходимая для этого работа будет равна 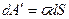. Работа по увеличению площади поверхности совершается против сил поверхностного натяжения, которые стремятся сократить, уменьшить поверхность. Поэтому работа самих сил поверхностного натяжения по увеличению площади поверхности жидкости будет равна:

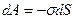(10-7)

Здесь коэффициент пропорциональности σ называется коэффициентом поверхностного натяжения и определяется величиной работы сил поверхностного натяжения по изменению площади поверхности на единицу. В СИ коэффициент поверхностного натяжения измеряется в Дж/м² .

Молекулы поверхностного слоя жидкости обладают избыточной по сравнению с глубинными молекулами, потенциальной энергией, которая прямо пропорциональна площади поверхности жидкости:

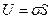(10-8)

Приращение потенциальной энергии поверхностного слоя связано только с приращением площади поверхности: 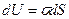. Силы поверхностного натяжения – консервативные силы, поэтому выполняется равенство: 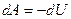. Силы поверхностного натяжения стремятся уменьшить потенциальную энергию поверхности жидкости. Обычно та энергия, которая может быть преобразована в работу, называется свободной энергией U_S. Поэтому можно записать 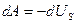. Используя понятие свободной энергии, можно записать формулу (10-8) так: 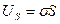. Используя последнее равенство можно определить коэффициент поверхностного натяжения как физическую величину, численно равную свободной энергии единицы площади поверхности жидкости .

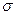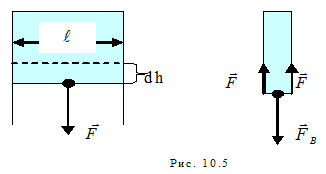Действие сил поверхностного натяжения можно наблюдать с помощью простого эксперимента над тонкой плёнкой жидкости (например, мыльного раствора), которая обволакивает проволочный прямоугольный каркас, у которого одна сторона может перемешаться (рис.10.5). Предположим, что на подвижную сторону, длиной ℓ, действует внешняя сила F_B , перемещающая подвижную сторону рамки равномерно на очень малое расстояние dh. Элементарная работа этой силы будет равна 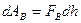, так как сила и перемещение сонаправлены. Поскольку плёнка имеет две поверхности и, то вдоль каждой из них направлены силы поверхностного натяжения F, векторная сумма которых равна внешней силе. Модуль внешней силы равен удвоенному модулю одной из сил поверхностного натяжения: 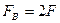. Минимальная работа, совершаемая внешней силой, равна по величине сумме работ сил поверхностного натяжения: 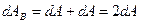. Величина работы силы поверхностного натяжения будет определяться так:

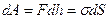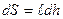, где . Отсюда 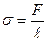. То есть коэффициент поверхностногонатяжения может быть определён как величина, равная силе поверхностного натяжения, действующей по касательной к поверхности жидкости, приходящейся на единицу длины линии раздела. Силы поверхностного натяжения стремятся сократить площадь поверхности жидкости. Это заметно для малых объёмов жидкости, когда она принимает форму капель-шариков. Как известно, именно сферическая поверхность имеет минимальную площадь при данном объёме. Жидкость, взятая в большом количестве, под действием силы тяжести растекается по поверхности, на которой она находится. Как известно, сила тяжести зависит от массы тела, поэтому её величина по мере уменьшения массы тоже уменьшается и при определённой массе становится сравнимой или даже много меньше величины силы поверхностного натяжения. В этом случае силой тяжести можно пренебречь. Если жидкость находится в состоянии невесомости, то даже при большом объёме её поверхность стремится к сферической. Подтверждение тому - знаменитый опыт Плато. Если подобрать две жидкости с одинаковой плотностью, то действие силы тяжести на одну из них (взятую в меньшем количестве) будет скомпенсировано архимедовой силой и она примет форму шара. При этом условии она будет плавать внутри другой жидкости.

Рассмотрим, что происходит с каплей жидкости 1, граничащей с одной стороны с паром 3, с другой стороны с жидкостью 2 (рис.10.6). Выберем очень малый элемент границы раздела всех трёх веществ dℓ. Тогда силы поверхностного натяжения на границах раздела сред будут направлены по касательным к контуру границ раздела и равны:

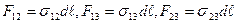(10-9)

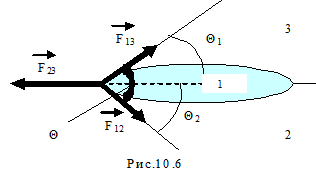Действием силы тяжести пренебрежём. Капля жидкости 1 находится в равновесии, если выполняются условия:

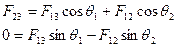(10-10)

Подставив (10-9) в (10-10), сократив на dℓ обе части равенств (10-10),возведя в квадрат обе части равенств (10-10) и сложив их, получим:

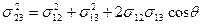, (10-11)

где 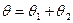- угол между касательными к линиям раздела сред, называется краевым углом.

Анализ уравнения (10-11) показывает, что при 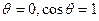получим 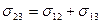и жидкость 1 полностью смачивает поверхность жидкости 2, растекаясь по ней тонким слоем (явление полного смачивания).

Аналогичное явление можно наблюдать и при растекании тонким слоем жидкости 1 по поверхности твёрдого тела 2. Иногда жидкость наоборот не растекается по поверхности твёрдого тела. Если 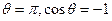, то 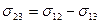и жидкость 1 полностью не смачивает твёрдое тело 2 (явление полного несмачивания). В этом случае есть только одна точка касания жидкости 1 и твёрдого тела 2. Полное смачивание или несмачивание являются предельными случаями. Реально можно наблюдать частичное смачивание, когда краевой угол острый ( 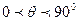) и частичное несмачивание, когда краевой угол тупой ( ).

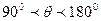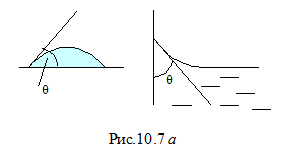
На рисунке 10.7 а приведены случаи частичного смачивания, а на рис.10.7 б приведены примеры частичного несмачивания. Рассмотренные случаи показывают, что наличие сил поверхностного натяжения граничащих 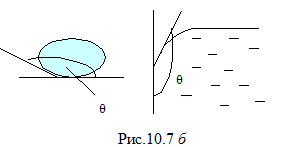жидкостей или жидкости на поверхности твёрдого тела приводит к искривлению поверхностей жидкостей.

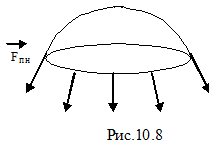Рассмотрим силы, действующие на кривую поверхность. Кривизна поверхности жидкости приводит к появлению сил, действующих на жидкость под этой поверхностью. Если поверхность сферическая, то к любому элементу длины окружности (рис.10.8) приложены силы поверхностного натяжения, направленные по касательной к поверхности и стремящиеся её сократить. Результирующая этих сил направлена к центру сферы.

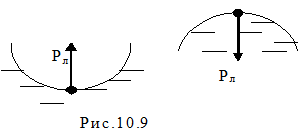
Отнесённая к единице площади поверхности эта результирующая сила оказывает дополнительное давление, которое испытывает жидкость под искривлённой поверхностью. Это дополнительное давление называется давлением Лапласа. Оно всегда направлено к центру кривизны поверхности. На рисунке 10.9 приведены примеры вогнутой и выпуклой сферических поверхностей и показаны давления Лапласа, соответственно.

Величина давления Лапласа для сферической, цилиндрической и любой поверхности соответственно имеет вид:

; ; .

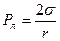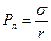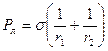Капиллярные явления

Пусть жидкость находится в каком-либо сосуде. Если расстояния между поверхностями, ограничивающими жидкость сравнимы с радиусом кривизны поверхности жидкости, то такие сосуды называются капиллярами. Явления, происходящие в капиллярах, называются капиллярными явлениями. К капиллярным явлениям относят капиллярный подъём жидкости и капиллярное сцепление между смачиваемыми поверхностями.

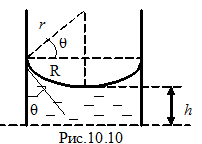
Наиболее простыми и часто используемыми капиллярами являются цилиндрические капилляры (рис.10.10). Поверхность жидкости в таких капиллярах является сферической. Пусть r - радиус кривизны поверхности жидкости, R – радиус капилляра, θ – краевой угол. В случае частичного смачивания жидкость будет подниматься по капилляру под действием давления Лапласа, до тех пор, пока его не скомпенсирует гидравлическое давление жидкости:

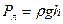, (10-12)

где ρ – плотность жидкости, g – ускорение силы тяжести, h – высота капиллярного подъёма. Радиус кривизны поверхности жидкости удобно выразить через радиус капилляра, который можно легко измерить: 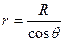. Подставляя давление Лапласа для сферической поверхности выражение (10-12), получим:

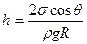(10-13)

В случае полного смачивания θ =0^о, cos θ =1, r = R и формула высоты капиллярного подъёма имеет вид:

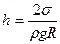(10-14)

При полном несмачивании θ=180^о, cos θ = - 1, и высота капиллярного подъёма будет отрицательной, то есть поверхность жидкости опустится на величину h (рис. 10.11).

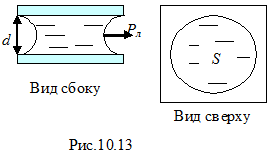
Интересно отметить, что в сообщающихся капиллярах высота уровня жидкости не одинакова. Наибольший капиллярный подъём наблюдается в самом узком капилляре, а наименьший – в самом широком капилляре (рис.10.12).

Для полного смачивания 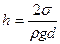. Капиллярные явления наблюдаются при подъёме воды к поверхности почвы, при использовании промокательной бумаги, тряпки, при подъёме керосина в фитилях и т.п.

С повышением температуры коэффициент поверхностного натяжения жидкостей уменьшается, а при критической температуре равен нулю. Коэффициент поверхностного натяжения жидкостей зависит также от плотности и молярной массы жидкости. Причём зависимость коэффициента поверхностного натяжения от температуры выражена тем сильнее, чем больше плотность жидкости и меньше её молярная масса. Для определения коэффициента поверхностного натяжения можно использовать полуэмпирическую формулу:

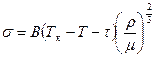(10-14)

Здесь В – постоянный коэффициент, практически одинаковый для всех жидкостей, Т_к – критическая температура, ρ- плотность жидкости, μ – её молярная масса, τ- небольшая величина размерности температуры. Формула (10-14) неприменима вблизи критической температуры. Коэффициент поверхностного натяжения водных растворов зависит от рода растворённого вещества. Одни вещества, например, такие как спирт, мыло, стиральные порошки, растворённые в воде, имеющие меньшую, чем у воды плотность, приводят к уменьшению коэффициента поверхностного натяжения и называются поверхностно активными веществами. Поверхностно активные вещества применяют в качестве смачивателей, флотационных реагентов, пенообразователей, диспергаторов- понизителей твёрдости, пластифицирующих добавок, модификаторов кристаллизации и т.п. Увеличение концентрации таких веществ приводит к уменьшению коэффициента поверхностного натяжения. Другие вещества, растворённые в воде, например, сахар, соль, приводят к увеличению плотности раствора и увеличивают коэффициент поверхностного натяжения. Увеличение концентрации таких веществ приводит к увеличению коэффициента поверхностного натяжения. Для экспериментального определения коэффициентов поверхностного натяжения используют несколько методов измерения: метод Ребиндера, метод капиллярных волн, метод капли и пузырька и др.

Твёрдые тела