Опытные законы идеального газа

Лекция №7

Молекулярно-кинетическая теория газов. Основные положения МКТ. Опытные законы идеального газа. Основное уравнение МКТ. Уравнение состояния идеального газа. Закон Максвелла для распределения молекул по скоростям. Барометрическая формула.

Основные положения МКТ.

Молекулярная физика изучает физические свойства макроскопических систем. Предметом её изучения являются молекулярные формы движения больших совокупностей молекул.

В основе молекулярной физики лежит понятие молекулы. Основные положения молекулярно-кинетической теории поясняют суть этой теории. Эти положения подтверждены практикой.

1. Все вещества состоят из частиц (молекул)

Опытное подтверждение этого положения:

· Смешивание разных жидкостей, например, воды и спирта, показывает, что объём смеси меньше суммарного объёма, занимаемого двумя жидкостями до их смешивания. Это можно объяснить тем, что между молекулами жидкостей есть пустоты, и при смешивании жидкостей молекулы одной из них проникают в свободное пространство между молекулами другой жидкости.

· Расширение тел при нагревании и сжатие при охлаждении также можно объяснить тем, что вещества состоят из молекул, расположенных друг от друга на некотором расстоянии. При нагревании расстояния между молекулами увеличиваются, а при охлаждении уменьшаются.

· Проявление дискретной структуры при наблюдении веществ под электронными или ионными микроскопами.

2. Частицы (молекулы) взаимодействуют друг с другом.

Факты, подтверждающие это положение:

· наличие сил притяжения и отталкивания;

· существование трех агрегатных состояний: из-за разного взаимодействия молекул проявляются разные свойства агрегатных состояний, отражённые в таблице:

газ	не имеет собственной формы и объема
жидкость	не имеет собственной формы, но имеет собственный объём
твердое тело	имеет собственную форму и объем

3. Частицы (молекулы) непрерывно и беспорядочно движутся

Некоторые факты, подтверждающие это положение:

· молекулы газа распространяются по всему объему сосуда;

· броуновское движение;

· диффузия.

Что представляют собой те частицы, из которых составлены вещества?

Молекула- это наименьшая частица вещества, сохраняющая все его химические свойства. Различают молекулу в физическом смысле (физическую молекулу), которую можно уподобить упругому шарику, и химическую молекулу, выраженную формулой атомного состава. Молекулы не всех веществ можно рассматривать как физические, например, молекулы веществ с ионной связью (в частности, NaCl – повареная соль). Это важно, когда рассматриваются соударения молекул или их тепловое движение. Поэтому в формулировке основных положений МКТ чаще всего используют термин «частица».

Размеры молекул очень малы. Если представить молекулу в виде малого шарика, то его радиус имеет порядок величины10 ^{– 8 см =10 – 10 м. Молекулы состоят из атомов. Частицы, образующие атомы - электроны и ядра. Принято считать, что электрон имеет радиус порядка величины 10 – 11 см = 10 – 13 м, а ядра имеют радиусы примерно} »10 ^{– 12} ÷ 10 ^{– 13 см = 10 – 14} ÷10 ^–15 м.

Массы атомов и молекул

В качестве единичной атомной массы m_ат принимается 1/12 массы атома ядра изотопа углерода :

Относительная молекулярная масса, или относительная масса молекулы, есть отношение массы молекулы к единичной атомной массе:

Аналогично определяют и относительную атомную массу.

Абсолютные значения атомных масс по порядку величины заключаются в пределах 10 ^–25 ÷ 10 ^–27 кг, а относительные атомные массы в пределах 1÷10². Пределы относительных молекулярных масс m_r от 1 до 10⁵.

Количество вещества. Количество вещества характеризуется числом его структурных элементов. В СИ оно выражается в молях. Моль является основной единицей измерения, так же как метр и секунда.

Моль равен количеству вещества рассматриваемой системы, которое содержит столько же структурных элементов, сколько атомов содержится в 0,012 кг изотопа углерода .

Понятие моля относится к числу структурных элементов вещества. Поэтому нужно говорить: «моль молекул», «моль атомов», «моль электронов» и т.п.

Таким образом, моль любого вещества содержит одинаковое число структурных элементов. Это число называется постоянной Авогадро или числом Авогадро:

Отсюда следует:

Молярная масса –масса одного моля молекул вещества.

Её определяют через относительную массу молекулы:

Число молей молекул n связано с числом молекул N некоторого вещества формулой:

, где - масса вещества.

Агрегатные состояния вещества

Наличие разных агрегатных состояний вещества объясняется различным взаимодействием молекул. На рис.7.1 приведена зависимость сил межмолекулярного взаимодействия от расстояния.

На больших расстояниях преобладает действие сил притяжения, на малых - отталкивания. По природе эти силы - электромагнитные. С энергетической точки зрения, чем больше кинетическая энергия атомов, тем сильнее тенденция к разъединению, отталкиванию; чем больше потенциальная энергия сцепления, тем больше тенденция к соединению.

Если суммарная кинетическая энергия атомов и молекул много больше суммарной потенциальной энергии их взаимного притяжения, то вещество находится в газообразном состоянии; если много меньше, то в твердом. Жидкое состояние образуется при примерном равенстве этих энергий.

Лекция №8

Статистика газов. Микроскопические и макроскопические явления. Статистический и термодинамический методы исследования. Идеальный газ как статистическая система многих частиц. Основы молекулярно-кинетической теории. Давление, объем и температура газа как обобщенные ха­рактеристики состояния газа. Явления переноса в газах. Столкновение молекул. Средняя длина свободного пробега молекул. Диффузия. Осмос. Теплопроводность. Вязкое трение.

8.1. Микроскопические и макроскопические явления. Статистический и термодинамический методы исследования. Идеальный газ как статистическая система многих частиц. Основы молекулярно-кинетической теории. Давление, объем и температура газа как обобщенные ха­рактеристики состояния газа.

Системой называют конечную область пространства с находящимися в ней физическими объектами исследования.

Граница системы может быть как материальной (стенки сосуда), так и воображаемой; неподвижной или движущейся; проницаемой или непроницаемой. Система характеризуется не только особенностями своей границы, но и физическими или химическими свойствами вещества, находящегося в занимаемой системой области пространства .

Макроскопическими системами называют системы, содержащие большое количество физических объектов. Термодинамические макроскопические системы содержат большое количество молекул (атомов, ионов). Различают разные виды термодинамических систем (ТС): закрытые, открытые, адиабатные и изолированные.

Закрытые ТС это системы, не обменивающиеся веществом с другими системами.

Открытые ТС это системы, обменивающиеся веществом и энергией с другими системами.

Адиабатные ТС это системы, в которых нет теплообмена с другими системами.

Изолированные ТС это системы, не обменивающиеся с другими системами ни энергией, ни веществом.

Для описания макросистем в молекулярной физике используют основные параметры состояния – температуру, давление, объём. Любое теоретическое описание реальных систем возможно только на основе той или иной модели, в которой учитывают определённые особенные свойства, а второстепенными пренебрегают. В молекулярной физике рассматривают следующие основные модели: идеальный газ, реальный газ, идеальная жидкость, реальная жидкость, твердое тело, плазма.

Макросистемы могут находиться в равновесном и неравновесном состоянии.

Равновесными состояниями называют такие, при которых макроскопические величины, описывающие поведение изолированной системы, остаются неизменными во времени и одинаковыми в пространстве.

В неравновесном состоянии макровеличины, характеризующие состояние системы, изменяются в пространстве и во времени, при этом в системе возникают потоки вещества и энергии (явления переноса).

Неравновесные состояния сложных систем изучают, используя методы физической кинетики.

Макроскопические системы могут быть линейными и нелинейными. В слабо неравновесных состояниях, где градиенты величин малы, переносимые потоки и силы, вызывающие их, линейно зависят от градиентов. В сильно неравновесных состояниях, где градиенты величин велики, потоки являются более сложными функциями градиентов.

При изучении состояния систем используют термодинамический и статистический подходы.

Термодинамический подход. Систему рассматривают без учета её внутренней структуры. При этом используют понятия и величины, относящиеся к системе в целом. Например, идеальный газ в состоянии равновесия характеризуют объёмом, давлением и температурой (V, P и T). Экспериментально устанавливают связь между этими величинами. Для термодинамического подхода характерно использование термодинамических потенциалов для описания систем, находящихся в равновесном или слабо неравновесном состоянии. Для сильно неравновесных нелинейных систем описание состояния через потенциалы невозможно.

Статистический подход. Динамическое описание системы, содержащей большое число частиц, невозможно. Для изучения макросистем применяют статистические методы, использующие понятия и величины, относящиеся не к отдельным частицам, а к большим совокупностям частиц. Законы поведения совокупностей большого числа частиц, использующие статистические методы, называются статистическими закономерностями. Эти закономерности, как и величины, описывающие состояние системы, зависят от того, в каком состоянии находится система: равновесном или неравновесном.

Диффузия в газах

Диффузией называется явление взаимного проникновения двух или нескольких соприкасающихся веществ. Каждый из компонентов смеси переходит из области с большей концентрации в область с меньшей концентрацией. При диффузии, таким образом, происходит перенос вещества. Диффузия в газах возникает и в том случае, если они неоднородны по концентрации или плотности (самодиффузия). Для количественного описания этого явления используют понятие диффузионного потока. Диффузионный поток можно выразить через массу переносимого вещества или через число молекул (или молей) переносимого вещества.

Диффузионный поток как поток массы определяется массой вещества, перенесённого через площадку dS, перпендикулярную направлению переноса, в единицу времени. Часто используют понятие плотности диффузионного потока. Плотность диффузионного потока определяется массой вещества, перенесённого через единичную площадку, перпендикулярную направлению переноса, в единицу времени. Плотность диффузионного потока равна:

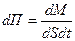, (8-13)

где dM- элемент массы вещества, переносимого через бесконечно малую площадку dS , перпендикулярную направлению переноса, за бесконечно малый промежуток времени dt.

Диффузионный поток как поток частиц определяется числом частиц вещества, перенесённого через площадку dS, перпендикулярную направлению переноса, в единицу времени. Плотность диффузионного потока определяется числом частиц вещества, перенесённого через единичную площадку, перпендикулярную направлению переноса, в единицу времени. В этом случае плотность диффузионного потока равна:

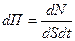, (8-14)

где dN- элементарное число частиц вещества, переносимого через бесконечно малую площадку dS, перпендикулярную направлению переноса, за бесконечно малый промежуток времени dt.

Основной закон диффузии – закон Фика:

плотность диффузионного потока какого-либо компонента вещества прямо пропорциональна градиенту концентрации (плотности) этого компонента со знаком «минус»:

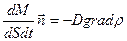(8-15)

Здесь 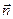- вектор положительной нормали к площадке, через которую переносится вещество; его направление совпадает с направлением переноса вещества. Градиент плотности grad - это вектор, который, характеризует быстроту изменения скалярной величины – плотности - в пространстве и направлен в сторону наиболее быстрого возрастания данной плотности. D - коэффициент диффузии. Знак «минус» показывает, что направление потока вещества противоположно градиенту плотности.

Градиент плотности можно записать так:

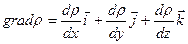, (8-16)

где 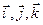- единичные вектора, направленные вдоль осей x,y,z, соответственно.

Для одномерного случая 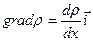и уравнение (8-15) может быть переписано в скалярном виде при условии, что направления векторов 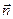и 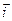совпадают:

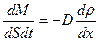(8-17)

Аналогично можно записать закон Фика и через поток частиц:

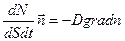(8-18)

Коэффициент диффузии численно равен плотности диффузионного потока при единичном градиенте концентрации (плотности) и СИ измеряется в .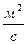

В идеальных газах механизм переноса вещества обусловлен соударениями молекул, поэтому, чем выше температура газа, тем больше диффузионный поток и коэффициент диффузии. Коэффициент диффузии, а точнее самодиффузии (диффузии вещества самого в себя, обусловленной неоднородностью концентрации) для идеальных газов можно выразить так:

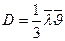(5-19)

Здесь 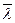- средняя длина свободного пробега молекул идеального газа, 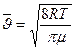- средняя арифметическая скорость молекул. При фиксированной температуре 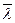обратно пропорциональна давлению, а скорость является постоянной, поэтому коэффициент диффузии. обратно пропорционален давлению. При фиксированном давлении 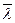прямо пропорциональна Т, а средняя арифметическая скорость ~ 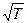, поэтому коэффициент диффузии в этом случае пропорционален .

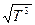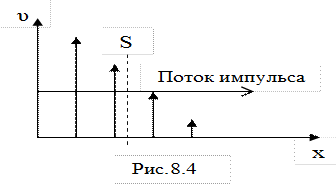
Вязкость газов

Вязкость газов – это свойство, благодаря которому выравниваются скорости упорядоченного движения разных слоёв газа. Можно дать и другое определение. Вязкость газов – это явление переноса, при котором происходит перенос импульса упорядоченного движения от слоёв, движущихся с большей скоростью, к слоям, движущимся с меньшей скоростью.. Переносимый импульс можно количественно оценить с помощью потока импульса, равного импульсу упорядоченного движения слоёв, переносимому через площадку dS, параллельную слоям и перпендикулярную к направлению переноса (рис.8.4), в единицу времени. Плотность элементарного потока импульса можно записать так:

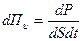(8-20)

Основной закон вязкости:

плотность потока импульса прямо пропорциональна градиенту скорости со знаком «минус».

Знак «минус» показывает, что направление потока импульса противоположно направлению градиента скорости упорядоченного движения.

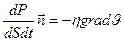(8-21)

Здесь 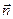- вектор положительной нормали к площадке S, через которую переносится импульс, его направление совпадает с направлением переноса импульса, 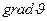- градиент скорости, направлен в сторону наиболее быстрого возрастания скорости, η- коэффициент динамической вязкости. Для одномерного случая, когда направления векторов 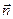и 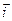совпадают:

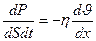(8-22)

Динамический коэффициент вязкости численно равен потоку импульса при единичном градиенте скорости. В СИ он измеряется в 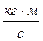или в Па^.с.

Для идеальных газов коэффициент динамической вязкости можно выразить следующим образом:

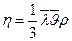(8-23)

Коэффициент вязкости зависит прямо пропорционально от 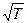и не зависит от давления, поскольку в формулу (8-22) входят как сомножители средняя длина свободного пробега, обратно пропорциональная давлению при фиксированной температуре, и плотность газа, прямо пропорциональная давлению.

Можно записать основной закон вязкости и через силу вязкого трения, которая направлена по касательной к слоям (к площадке S), используя второй закон Ньютона, согласно которому 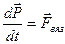. Для одномерного случая получим:

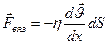(8-24)

Явление вязкости бывает стационарным и нестационарным. О стационарной вязкости говорят, когда градиент скорости поддерживают постоянным. Нестационарная вязкость происходит с изменением градиента, в результате выравниваются скорости взаимодействующих слоёв.

Для измерения коэффициента вязкости используют приборы – вискозиметры. Для измерения коэффициента вязкости необходимо, чтобы движение газа было ламинарным, то есть плавным, без завихрений. Этого можно достичь в очень узких трубках – капиллярах. Поэтому такие вискозиметры, в которых используют капилляры, называют капиллярными вискозиметрами.

Теплопроводность газов

Явление возникновения потока тепла в газе (или любом другом веществе) называется теплопроводностью. Перенос количества теплоты можно описать с помощью потока теплоты.

Потоком теплоты называется количество теплоты, перенесённое через площадку, перпендикулярную направлению переноса, в единицу времени. Плотность потока теплоты, как количество теплоты, перенесённое через единичную площадку, перпендикулярную направлению переноса, в единицу времени, можно выразить так:

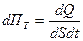(8-25)

Основной закон теплопроводности – закон Фурье:

плотность потока теплоты прямо пропорциональна градиенту температуры со знаком «минус»:

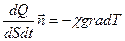(8-26)

Здесь 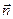- вектор положительной нормали к площадке dS, через которую переносится количество теплоты, его направление совпадает с направлением переноса количества теплоты, 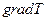- градиент температуры, направлен в сторону наиболее быстрого возрастания температуры, χ- коэффициент теплопроводности. Для одномерного случая, когда направления векторов 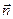и 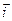совпадают:

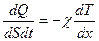(8-27)

Коэффициент теплопроводности численно равен потоку теплоты при единичном градиенте температуры. Для идеальных газов он может быть выражен так:

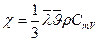(8-28)

Здесь С_mV – удельная теплоёмкость при постоянном объёме. Коэффициент теплопроводности прямо пропорционален 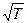и не зависит от давления. В СИ коэффициент теплопроводности измеряется в .

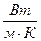Лекция №9

Основы термодинамики. Распределение энергии по степеням свободы молекул. Внутренняя энергия. Первое начало термодинамики. Работа газа при его расширении. Теплоемкость. Уравнение Майера. Адиабатический и политропный процессы. Второе начало термодинамики. Круговые, необратимые и обратимые процессы. Принцип действия тепловой машины. Цикл Карно и его КПД. Энтропия. Второе начало термодинамики и его статистический смысл. Связь энтропии и вероятности.

Внутренняя энергия

Под внутренней энергией системы понимают полную суммарную энергию всех её структурных элементов.

Внутренняя энергия идеального газа складывается только из кинетических энергий молекул, так как потенциальной энергией их взаимодействия можно пренебречь.

Внутренняя энергия идеального газа U для любого количества молей n может быть определена через среднюю кинетическую энергию, определяемую формулой (9-3). Так как средняя кинетическая энергия идеального газа зависит только от температуры и числа степеней свободы молекулы, то и внутренняя энергия идеального газа также зависит от температуры и числа степеней свободы молекулы:

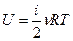(9-4)

Изменение внутренней энергии идеального газа определяется только изменением температуры и не зависит ни от давления, ни от объёма:

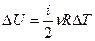(9-5)

Изменить внутреннюю энергию газа можно, например, совершив над ним работу. Но независимо от того, каким способом совершают работу, изменение внутренней энергии идеального газа зависит только от изменения температуры. Другими словами, изменение внутренней энергии зависит только от параметров начального и конечного состояния, а именно от температуры начального Т₁ и конечного состояния Т _{2 ,} и не зависит от процесса перехода из начального в конечное состояние. Поэтому внутренняя энергия – функция состояния. Если газ вернули в первоначальное состояние, то изменение внутренней энергии равно нулю.

Для элементарного процесса 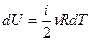. Можно внести постоянные ν и R под знак дифференциала 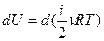. Таким образом, изменение внутренней энергии является полным дифференциалом величины, стоящей в скобках, и этот факт может служить признаком функции состояния.

9.3. Работа газа при его расширении

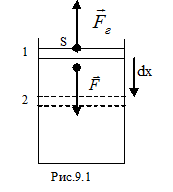
Рассмотрим сжатие идеального газа, находящегося под поршнем (рис.9.1). Под действием внешней силы 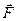переместим поршень на бесконечно малую величину 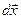, настолько малую, что будем считать силу 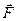постоянной. Назовём работу постоянной силы по перемещению поршня на бесконечно малую величину элементарной работой и обозначим 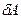. Элементарная работа может быть определена как работа постоянной силы через скалярное произведение силы на перемещение:

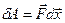(9-6)

Поскольку направление силы и перемещения совпадают, то 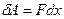. Газ, находящийся под поршнем, препятствует сжатию и давит на поршень силой 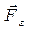, равной по величине, противоположной по направлению и приложенной к поршню (рис.4.1). Элементарная работа самого газа 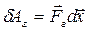. Так как сила 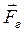и перемещение 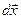направлены в противоположные стороны, работа самого газа при равномерном сжатии отрицательна и равна по величине работе внешней силы, сжимающей газ 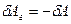. Сила, действующая на единицу площади поверхности поршня S со стороны газа, есть давление газа Р. Поэтому можно выразить величину силы 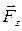через давление: 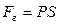. Тогда элементарная работа газа будет равна: 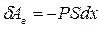. Но 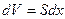есть величина приращения объёма газа. Тогда элементарная работа газа равна:

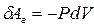, (9-7)

а работа внешней силы по сжатию газа равна .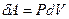

Для определения работы по перемещению поршня на значительную величину 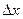, в результате которой объём газа изменяется на 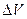, нужно учесть процесс, происходящий с газом. Работу в этом случае определяют через интеграл:

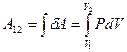(9-8)

Работа газа (или над газом) зависит от процесса (т.е. от последовательности промежуточных состояний) и поэтому является функцией процесса. Работа не является полным дифференциалом, отсюда и обозначение элементарной работы 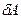, а не dA.

Рассмотрим работу, совершаемую газом, при различных процессах. Будем обозначать в дальнейшем элементарную работу газа просто через 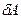и считать её положительной, если газ расширяется ( 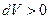), и отрицательной, если газ сжимают ( ).

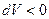Рассмотрим изохорический процесс. При изохорическом процессе объём газа не изменяется, приращение объёма равно нулю, следовательно, работа газа равна нулю.

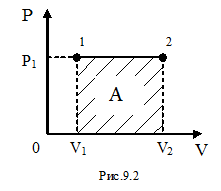
Поскольку работу в любом случае можно определить, пользуясь формулой (9-8), для математической интерпретации работы удобно изображать любой процесс на диаграмме (P,V) . Работа на такой диаграмме равна площади фигуры под кривой, изображающей тот или иной процесс, происходящий с газом.

Рассмотрим изобарический процесс (рис. 9.2). Используя формулу (9-8) найдём работу газа при переходе из состояния 1 в состояние 2: .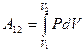

Так как для данного количества вещества давление остаётся постоянным при изобарическом процессе, то его можно вынести за знак интеграла, тогда получим :

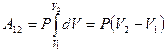. Обозначим 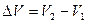. С учётом этой записи работа при изобарическом процессе определяется по формуле:

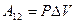(9-9)

Используя рис.9.2, можно записать работу через указанные параметры состояния: 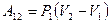. Такую же формулу мы получим, находя площадь заштрихованного прямоугольника. Часто бывает удобно выражать работу через изменение температуры. Для этого нужно использовать уравнение состояния идеального газа (уравнение Менделеева – Клапейрона) для 1 и 2 состояни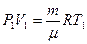й: и 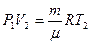. Вычитая из второго уравнения первое, получим:

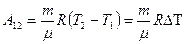(9-10)

При изобарическом сжатии конечный объём меньше начального и работа газа отрицательна, то есть газ препятствует сжатию.

Формула (9-7) позволяет выразить физический смысл молярной постоянной R . Для одного моля вещества ( 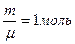) работа определяется как 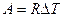. Отсюда ясен физический смысл R , которая определяется работой изобарического расширения одного моля идеального газа при изменении температуры на один кельвин.

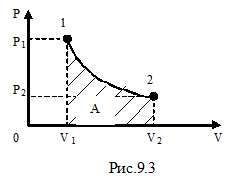Рассмотрим изотермический процесс (рис.9.3). При изотермическом процессе температура остаётся постоянной, а давление и объём связаны между собой обратно пропорциональной зависимостью. В этом случае, используя формулу (9-8) для определения работы, уже нельзя вынести давление за знак интеграла. Давление выразим из уравнения Менделеева – Клапейрона: 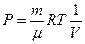. Подставим правую часть этого уравнения в (9-8) и вынесен за знак интеграла все постоянные:

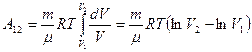. Учитывая, что разность логарифмов есть логарифм отношения, получим:

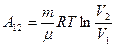(9-11)

Используя закон Бойля- Мариотта: 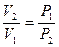, можем выразить работу и через отношение давлений:

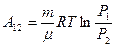(9-12)

Рассмотренные примеры подтверждают, что работа является функцией процесса.

Первое начало термодинамики

Первое начало термодинамики учитывает энергетический баланс системы. В этом суть первого начала термодинамики. Можно сказать, что первое начало термодинамики является законом сохранения энергии для термодинамических систем.

Для элементарного процесса первое начало термодинамики можно записать следующим образом: 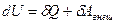. Работа самого газа связана с работой внешних сил равенством 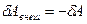. Тогда математическая запись первого начала термодинамики будет иметь вид: 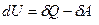. Однако в тех случаях, когда происходит теплообмен и система получает (или отдаёт тепло), удобно записывать первое начало в виде:

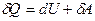(9-13)

Адиабатный процесс

Существует достаточно много явлений, например, нагревание ручного насоса при накачивании шин, понижение температуры воздуха после извержения вулкана, при котором быстро расширяются газы, изменение температуры воздуха при сильных порывах ветра, процессы, происходящие с веществом, заключённым в теплоизолирующую оболочку, распространение звуковых волн и многие другие, объяснить которые можно, используя понятие адиабатного процесса.

Адиабатный процесс это процесс, происходящей без теплообмена системы с окружающей средой.

Реализовать такой процесс на практике можно, быстро сжимая или расширяя газ, или заключая его в теплоизолирующую оболочку (термос, сосуд Дьюара). При адиабатном процессе 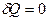, а, следовательно, первое начало термодинамики будет иметь вид: 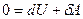или 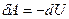. При адиабатном расширении газ совершает механическую работу за счёт убыли собственной внутренней энергии. При адиабатном сжатии внутренняя энергия газа растёт за счёт работы внешних сил, сжимающих его.

Получим уравнение адиабаты, используя первое начало термодинамики. Приращение внутренней энергии можно записать через молярную изохорическую теплоёмкость: 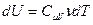, элементарную работу – через давление и приращение объёма: 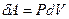. Получим

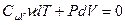(9-23)

Исключим из этого уравнения приращение температуры, используя уравнение Менделеева - Клапейрона 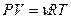. Продифференцируем его и получим: 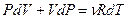, отсюда выразим приращение температуры 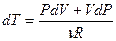и подставим его в (9-23), после приведения подобных получим: 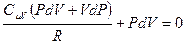. Заменим в этом равенстве R на 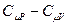, приведём к одному знаменателю, раскроем скобки и получим:

.

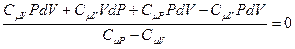Так как знаменатель не равен нулю, то равенство будет выполняться, если числитель равен нулю. После приведения подобных получим:

.

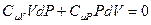Обозначим отношение теплоёмкостей 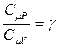. Это отношение g принято называть показателем адиабаты или коэффициентом Пуассона. После введения g получим:

.

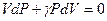Поделим обе части равенства на PV и получим уравнение с разделяющимися переменными: 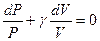. Проинтегрируем это уравнение и получим: 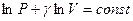или 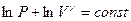. Воспользуемся свойством логарифмов: сумму логарифмов можно представить как логарифм произведения: 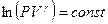. После потенцирования получим уравнение адиабаты:

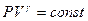(9-24)

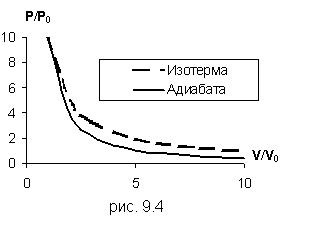
Это уравнение показывает, что при адиабатном процессе с изменением объёма давление изменяется на большую величину, чем при изотермическом процессе, поскольку 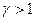. Рис.9.4, на котором приведены изотерма (пунктирная линия) и адиабата (сплошная линия) для случая, когда начальные параметры состояния газа одинаковы, наглядно показывает это.

Используя уравнение состояния идеального газа, можно записать уравнение адиабаты через объём и температуру. Для этого нужно из уравнения состояния идеального газа выразить давление и подставить в уравнение (9-24). После преобразований получим:

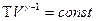(9-25)

Можно записать уравнение адиабаты через давление и температуру, выразив из уравнения состояния идеального газа, объём через давление и температуру:

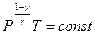(9-26)

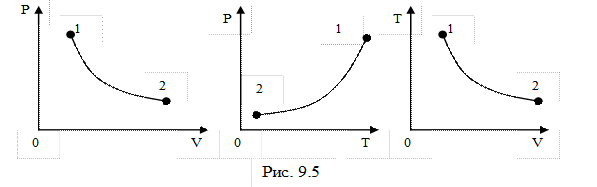При адиабатном процессе все три параметра состояния изменяются. Это изменение выражено формулами (9-24), (9-25), (9-26).

Процесс адиабатного расширения изображён на рис.9.5 При адиабатном расширении газ совершает работу за счёт убыли собственной внутренней энергии: 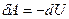. Работу адиабатного процесса проще всего рассчитать через изменение внутренней энергии: 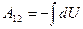. Поскольку внутренняя энергия идеального газа – функция состояния и зависит только от температуры, то изменение внутренней энергии, а, следовательно, и работу можно найти по формуле:

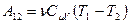(9-27)

Работу газа при адиабатном процессе можно определить и через элементарную работу: