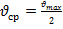Баланс сил при движении вязкой несжимаемой жидкости.

Рассмотрим в нестационарном потоке вязкой несжимаемой жидкости в некоторый момент времени весьма малый, но конечный объём, в котором все векторы скорости параллельны друг другу и направлены вдоль оси Oz. Выделим в этом объёме элементарный параллелепипед, грани которого сориентированы по соответствующим осям координат. Будем считать, что скорость меняется только по оси х, причём с ростом х скорость уменьшается.

Вывод математической зависимости, описывающей распределение скоростей и давлений:

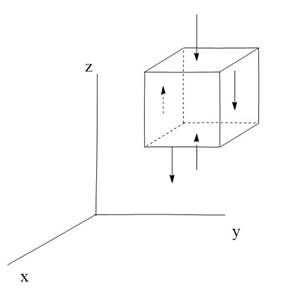1) выделяется элементарный объем жидкости[ДЦ1] , грани ориентированы по трём осям

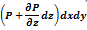
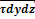
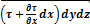
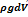
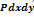
2) рассматривается баланс сил

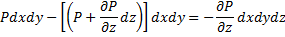
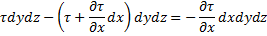
Сумма проекций всех сил:

→

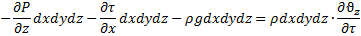
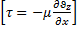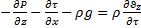
Получаем:

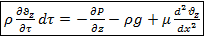!! Проекция только на ось Oz, скорость изменяется только по х.

;

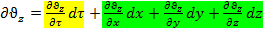Жёлтым – локальная составляющая, зелёным – конвективная составляющая

Учитывая соотношения , , 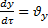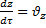и разделяя обе части равенства на dτ, получим выражение для полной (субстанциональной) производной:

;

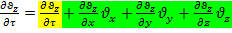Жёлтым – временная составляющая, зелёным – пространственная составляющая.

Если рассматривать скорости, направленные произвольно, то уравнение пополнится выражениями для изменения проекций скорости на оси х и у. Получена система уравнений Навье-Стокса

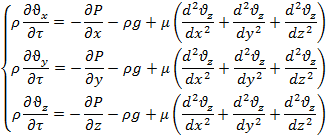
С помощью приведённых уравнений, а также выведенного ранее уравнения неразрывности, можно рассчитать распределение давлений и скоростей в объёме жидкости

Уравнение движения Эйлера применимы только для идеальной жидкости:

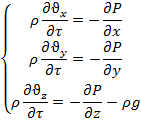
В стационарных условиях «работают» уравнения Эйлера:

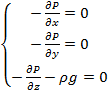В полных дифф.-лах: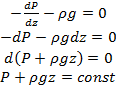

Таким образом, приходим к заключению: удельная потенциальная энергия покоящейся жидкости - величина постоянная.

Мы пришли к основному уравнению гидростатики: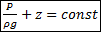

Основными характеристиками движущейся жидкости являются расход и средняя скорость потока.

Режимы течения жидкостей.[ДЦ2]

Ламинарное (вязкое) течение

Для данного режима характерно независимое течение слоёв жидкости, скорость которого на оси трубопровода достигает максимального значения. На стенках, наоборот, скорость течения при ламинарном режиме принимает нулевое значение.

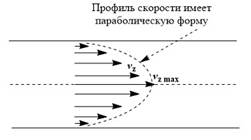Профиль распределения скорости в потоке при ламинарном течении:

Максимальную скорость можно рассчитать по формуле: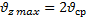

Течение с завихрениями (турбулентное)

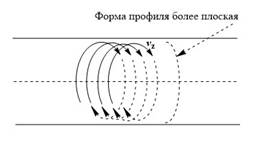Профиль распределения скорости в потоке при турбулентном течении:

Усреднённая по времени скорость рассчитывается по формуле: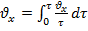

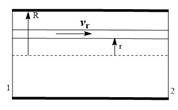
Пограничный слой

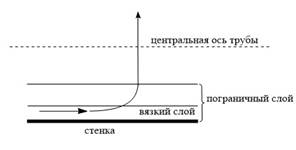У стенки трубы при любом виде течения существует некий пограничный слой.

В пограничном слое происходит уменьшение скорости. Течение в нём постепенно приближается к ламинарному. Скорость изменяется градиентно только в вязком слое, проходящем непосредственно у стенки трубы. Несмотря на незначительную толщину пограничного слоя по сравнению с потоком жидкости в трубе оказываемое его влияние на перенос жидкости значительно.

Переход турбулентного течения в ламинарное обеспечивает комплекс величин, объединенный в критерий Ренольца:

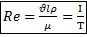, где ;

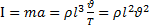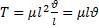
Примечание: в расчетах величину l (линейную характеристику) заменяют на эквивалентный диаметр смачиваемой поверхности - 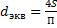(где S – площадь смачиваемой поверхности,

П – её периметр) или гидравлический радиус -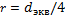

Если силы инерции малы, а силы трения превалируют, величина критерия невелика, и наоборот.

Величины критерия Ренольца для труб:

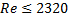– ламинарный режим; 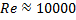– переходное состояние;

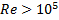– турбулентный режим;

Уравнения Пуазейля. Закон Стокса.

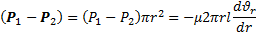
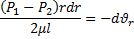
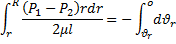
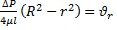- скорость в произвольном сечении трубы;

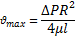
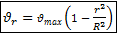- закон Стокса

Уравнение расхода:

; →
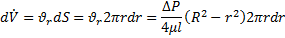
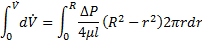
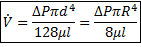
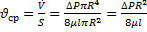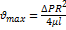